| | |
| | | |
| |
| | |
| | | |
| |
| | |
Mathematik ist... Ja, was ist Mathematik eigentlich? Das ist gar nicht so leicht zu sagen!
Wenn Sie die Gelegenheit haben, fragen Sie doch ein paar Mathematiker und Mathematikerinnen
(oder Mathematik-LehrerInnen) danach!
Sie werden ganz verschiedene Antworten bekommen. Beispielsweise "Mathematik beschäftigt sich
mit formalen Strukturen und quantitativen, d.h. durch Zahlen ausdrückbaren Beziehungen"
oder "Mathematik ist die Kunst, mit Hilfe exakten logischen Schließens aus bekannten Gegebenheiten
neue, bislang unbekannte Wahrheiten zu entdecken". Vielleicht hören Sie auch eine
Aussage wie "Mathematik handelt nicht von der realen Welt, sondern beschäftigt sich mit
idealisierten Denkmodellen" oder gar "Mathematik ist die Lehre von der Umformung von Zeichenketten".
All diese Aussagen haben auf ihre Weise recht, auch diese:
"Ein Mathematiker ist eine Maschine, die Kaffee in Theoreme umwandelt"
oder "Mathematik ist, was Mathematiker betreiben".
In jedem Fall ist es tatsächlich so, dass sich Mathematik zunächst auf ideale Gedankenkonstruktionen
bezieht. Diese werden von MathematikerInnen aus aller Welt weiterentwickelt
(wobei die Entscheidung, MathematikerIn zu werden, oft aus purer Freude an der Konstruktion und Analyse formaler Strukturen
erfolgte). Andererseits sind viele der mathematischen Begriffe und Methoden entwickelt worden,
um mehr von der Welt zu verstehen. So sind die physikalischen Naturgesetze in der Sprache der
Mathematik formuliert, und mittlerweile spielt die Mathematik auch in der Chemie und der
Biologie eine entscheidende Rolle. Mathematische Probleme ergeben sich, wenn technische oder
wirtschaftliche Systeme untersucht werden. Zwischen den beiden Triebkräften,
der "theoretischen" und der "angewandten" Motivation,
besteht eine ständige gegenseitige Beeinflussung und Stimulierung.
Während der letzten zwei Jahrtausende hat sich die Mathematik zu einer eigenständigen
Wissenschaft entwickelt, die in zahlreiche Spezialgebiete aufgefächert ist.
Zwischenzeitlich wurde sie sogar als "Königsdisziplin"
betrachtet, doch heute steht sie gleichberechtigt neben den anderen Wissenschaften.
Von diesem Standpunkt aus betrachtet ist Mathematik eine kulturelle Errungenschaft,
die nicht durch ein einfaches Statement umfassend charakterisiert werden kann.
Anstatt sich auf eine genaue Charakterisierung zu versteifen, was Mathematik ist, fällt es
leichter, einige weit verbreitete Ansichten über Mathematik abzuklopfen und
Verkürzungen zurechtzurücken, um grobe Missverständnisse
zu vermeiden.
Was Mathematik (eher) nicht ist
| | | |
| |
| | |
Über die Mathematik gibt es zahlreiche Anschauungen, die meist der Erfahrung
mit dem eigenen, bisher erhaltenen Unterricht entspringen.
Vielleicht kommt Ihnen diese Aussage bekannt vor:
"Mathematik ist gleichbedeutend mit Rechnen oder Rechentechnik. Das Lösen einer mathematischen Aufgabe
besteht darin, die für das gestellte Problem zuständige Formel oder das passende Verfahren
zu finden und mit deren Hilfe eine Rechnung durchzuführen. Am Ende kommt eine Zahl heraus,
das Ergebnis oder Resultat. Es wird unterstrichen, und damit ist die Aufgabe
gelöst."
Als Klarstellung ist dazu zunächst zu sagen, dass Rechentechniken sehr wohl eine unentbehrliche Hilfe bei der Lösung
mathematischer Aufgaben sind. Formeln, Rechenregeln und Berechnungsweisen – in einem vernünftigen
Ausmaß – zu kennen und anwenden zu können, ist Teil der Allgemeinbildung und
überdies in der Praxis etlicher Berufe notwendig.
Ohne sie könnten wir nur sehr wenige mathematische Probleme lösen.
Dennoch geht es im Kern auch um etwas Anderes: Zur Mathematik gehört vor allem das
Erfassen und Analysieren der Struktur von Problemen, das Entwickeln von
Lösungsstrategien, die Nutzung bekannter Sachverhalte, um neue Problemstellungen
bearbeiten zu können. Es geht also um das Finden der Lösungswege.
Es geht um das Verstehen, warum gerade diese oder jene
Rechenschritte zur Lösung eines Problems durchgeführt werden. Es geht darum,
zu überlegen, ob man auch auf anderem Weg zum Ziel hätte kommen können.
Mit einem Wort: Es geht darum, Erkenntnisse zu erzielen!
Diese – für die Mathematik typischen – Tätigkeiten erfordern eine
gewisse Kreativität. Sie fallen nicht einfach unter das Stichwort "rechnen". Eher können sie
durch Begriffe wie "suchen und finden", "erfassen und verstehen" sowie "analysieren, argumentieren,
begründen und beweisen" charakterisiert werden. Hinzu kommt noch die Übersetzung
von Problemen, die aus dem Alltag oder einem andern Fachgebiet stammen, in die mathematische
Sprache (das "Idealisieren" und "Modellieren") und schließlich das Rückübersetzen
mathematischer Ergebnisse in den Kontext, aus dem die Fragestellung stammt, um sie
sachgemäß beantworten und vielleicht auch "diskutieren und bewerten" zu können.
Das war jetzt eine lange Liste von Dingen, die Ihnen vielleicht unangenehm und allzu arbeitsaufwändig
erscheinen, die aber – jeweils in kleinen Dosen – auch von SchülerInnen im
Mathematikunterricht verlangt werden! Schon regt sich Widerstand:
"Ich will's nicht verstehen – ich möchte nur wissen,
wie's geht!"
Wie viele Mathematik-NachhilfelehrerInnen haben nicht über diesen Satz geklagt!
Wir werden weiter unten, beim Versuch, Ihnen einige Tipps zum
Lernen nahezubringen, ein bisschen mehr über diese Einstellung sagen. Hier
genügt der Hinweis, dass sie den Charakter von Mathematik grob verkürzt: Auch das "Verstehen" ist
eine mathematische Kompetenz, nicht nur das "Wissen, wie's geht".
|
| | |
| |
| | |
| Wie perfekt ist die Mathematik? |
| | | |
Zum Seitenanfang | |
| | |
Nach dieser ersten Orientierung, was Mathematik ist und worauf sie (eher) nicht verkürzt werden sollte,
wollen wir uns die Natur der Mathematik etwas näher ansehen. Mathematik gilt als
die logische Denktätigkeit par excellence – eine Methode, die
nie irrt. Wie "perfekt" ist die Mathematik tatsächlich, wie gut funktioniert sie?
In gewisser Hinsicht funktioniert die Mathematik hervorragend gut, in anderer Hinsicht funktioniert sie nur so gut
wie die Modelle, mit denen wir sie füttern,
und in einer dritten Hinsicht wiederum funktioniert sie so gut, dass wir Gefahr laufen,
sie zu vergessen. Anhand eines Beispiels wollen wir Ihnen nun diese drei Aspekte näher bringen,
um danach eine Antwort auf die Frage, wieso wir eigentlich Mathematik lernen und verstehen sollen,
zu geben.
Innermathematische Themen
| | | |
| |
| | |
Da gibt es zunächst die so genannten innermathematischen Themen und Problemstellungen.
Das sind solche, die von "abstrakten" Dingen handeln, die in der Regel sofort als der mathematischen
Sphäre zugehörig erkannt werden, und die keine realen Objekte bezeichnen,
sondern idealisierte Gedankenkonstruktionen. Natürlich kann darüber diskutiert werden, ob
mathematische Vorstellungen nicht auch in einem gewissen Sinn "real" sind oder zumindest aus der
"wirklichen Welt" stammen, aber darum geht es uns hier nicht.
Beispiel:
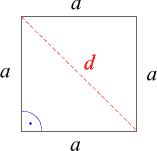 Jemand könnte auf die Idee kommen,
zu fragen, um welchen Faktor die Diagonale eines Quadrats länger ist als seine
Seitenlänge. (Schon vor langer Zeit sind Menschen auf die Idee gekommen, diese und
ähnliche Fragen zu stellen).
Jemand könnte auf die Idee kommen,
zu fragen, um welchen Faktor die Diagonale eines Quadrats länger ist als seine
Seitenlänge. (Schon vor langer Zeit sind Menschen auf die Idee gekommen, diese und
ähnliche Fragen zu stellen).
Das ist ein typisches innermathematisches Problem: Unter einem "Quadrat" dürfen wir uns hier
nicht etwa ein aus realer Materie bestehendes "quadratisches" Objekt (wie zum Beispiel
ein sorgfältig zugeschnittenes Stück Papier) vorstellen, denn kein aus
realer Materie bestehendes Objekt ist exakt quadratisch!
Das Quadrat als geometrische Figur in der Ebene, die von vier gleich langen
Strecken begrenzt wird, die einander in rechten Winkeln schneiden,
ist ein Gedankenobjekt. Auch Begriffe wie Ebene, Strecke, rechter Winkel,
ja sogar die Formulierung "gleich lang", verweisen auf
gedankliche Idealkonstruktionen und nicht auf reale Dinge. Reale Dinge können
höchstens näherungsweise "quadratisch" oder "gleich lang" sein.
| | | |
| |
| | |
Die Antwort auf das Problem der Quadratdiagonalen kennen Sie vielleicht bereits:
Die Diagonale ist um den Faktor √2 länger als die
Seitenlänge,
wobei √2 (ausgesprochen: "Wurzel aus 2") die Quadratwurzel aus 2 ist,
d.h. jene positive Zahl, die mit sich selbst multipliziert genau 2 ergibt.
(Der Beweis benutzt den Satz von Pythagoras – siehe den Exkurs rechts).
Ebenso wie alle anderen Zutaten dieses Problems ist auch die "Wurzel aus 2" ein gedankliches Konstrukt.
Ihre Dezimaldarstellung beginnt mit
|
√2 =
1.41421356237309504880168872420969807856967...
|
|
|
(1) |
und geht immer weiter, ohne Ende.
Die meisten Begriffe, die Sie in Zusammenhang mit der Mathematik bereits kennen gelernt haben,
und auch die meisten, die Sie noch kennen lernen werden,
gehören in den Bereich der innermathematischen Themen: Längen, Winkeln, Abstände,
Dreiecke, Quadrate, Kreise (überhaupt geometrische Figuren jeder Art), Zahlen, Quadratwurzeln,
Gleichungen, Funktionen, Differenzieren und Integrieren, ja sogar der Begriff der Wahrscheinlichkeit.
Es sind dies alles Objekte, mit denen sich exakt manipulieren lässt!
In diesem Bereich der idealen Gedankenkonstruktionen, mit denen sich exakt manipulieren lässt,
ist die Mathematik unschlagbar! Dort entfaltet sie ihre volle Stärke, ist einfach perfekt.
Zwar gibt es besonders schwierige mathematische Probleme, die (heute, d.h. auf der Basis unseres gegenwärtigen
Wissensstandes) als ungelöst gelten. Weiters sind mathematische Tatsachen nicht ganz so
objektiv und "wahr", wie es auf den ersten Blick erscheinen mag – wir werden
weiter unten unter dem Stichwort Gödel noch etwas dazu sagen.
Aber gemessen an dem, was uns hier interessiert, sind das Kleinigkeiten:
Mathematik ist ein Musterbeispiel für Exaktheit und Logik, ja die exakte Wissenschaft
schlechthin. Als Rache dafür, dass sie in ihrem ureigensten Bereich nicht von realen
Dingen handelt, sondern von formalen Gedankenkonstruktionen, wird sie in der Regel nicht als
Naturwissenschaft, sondern als Formalwissenschaft bezeichnet.
Mathematische Idealisierung und Modellierung
| | | |
Satz von Pythagoras im
Themen aus der
klassischen
Geometrie
| |
| | |
Neben den innermathematischen Themen gibt es
Fragestellungen und Probleme, die von "außen", d.h. entweder aus dem Alltagsleben oder
von einem anderen Fachgebiet, an die Mathematik herangetragen werden.
Wir sprechen in diesen Zusammenhängen auch von angewandter Mathematik, was aber
nicht darüber hinwegtäuschen sollte, dass sich hier ein Problem auftut:
Damit die Mathematik derartige Problemstellungen bearbeiten kann,
müssen sie zunächst in die mathematische Sprache
übersetzt, d.h. als innermathematische Probleme formuliert werden.
Eigentlich ist "übersetzen" nicht – oder nicht immer – das
richtige Wort, denn um eine Sache mathematisch zu formulieren, müssen ihr
da und dort Unebenheiten abgeschliffen, Idealisierungen vorgenommen und Unwägbarkeiten
ignoriert werden.
Beispiel:
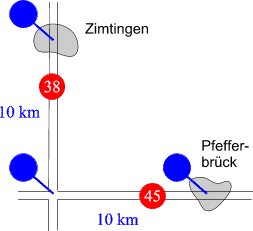 Die Ortschaft Zimtingen liegt an der nord-südlich verlaufenden Bundesstraße 38, die Ortschaft Pfefferbrück
liegt an der an der west-östlich verlaufenden Bundesstraße 45.
Wie in der nebenstehenden Straßenkarte verzeichnet, ist
die Kreuzung der zwei Bundesstraßen von beiden Ortschaften jeweils 10 Kilometer
entfernt. Um mit dem Auto von einem Ort zum anderen zu fahren, müssen daher 20 Kilometer
zurückgelegt werden. Nun kommt der Plan auf, eine direkte, gerade verlaufende Verbindungsstraße
von Zimtingen nach Pfefferbrück zu bauen. Frage: Wie lang wird sie sein?
(Die Antwort auf diese Frage ist in zweifacher Hinsicht von Interesse: Sie
gibt an, um wie viel schneller man dann von der einen in die andere Ortschaft gelangen kann,
und sie ist die Grundlage für die Kalkulation der anfallenden Baukosten).
Die Ortschaft Zimtingen liegt an der nord-südlich verlaufenden Bundesstraße 38, die Ortschaft Pfefferbrück
liegt an der an der west-östlich verlaufenden Bundesstraße 45.
Wie in der nebenstehenden Straßenkarte verzeichnet, ist
die Kreuzung der zwei Bundesstraßen von beiden Ortschaften jeweils 10 Kilometer
entfernt. Um mit dem Auto von einem Ort zum anderen zu fahren, müssen daher 20 Kilometer
zurückgelegt werden. Nun kommt der Plan auf, eine direkte, gerade verlaufende Verbindungsstraße
von Zimtingen nach Pfefferbrück zu bauen. Frage: Wie lang wird sie sein?
(Die Antwort auf diese Frage ist in zweifacher Hinsicht von Interesse: Sie
gibt an, um wie viel schneller man dann von der einen in die andere Ortschaft gelangen kann,
und sie ist die Grundlage für die Kalkulation der anfallenden Baukosten).
Mit den obigen Angaben als solchen kann die Mathematik zunächst gar nichts anfangen.
Schließlich sind Worte wie "Ortschaft" und "Bundesstraße" keine mathematischen
Begriffe. Um ein mathematisches Modell der beschriebenen Situation zu entwickeln,
können wir beispielsweise so vorgehen:
- Die beiden Bundesstraßen werden als aufeinander normal stehende Geraden idealisiert.
Die Kreuzung der beiden Bundesstraßen wird dann zum Schnittpunkt der beiden Geraden.
- Die Ortschaften Zimtingen und Pfefferbrück werden als Punkte auf den Geraden angesehen.
- Der Abstand zwischen dem Punkt "Kreuzung" und dem Punkt "Zimtingen" beträgt 10 Kilometer.
- Der Abstand zwischen dem Punkt "Kreuzung" und dem Punkt "Pfefferbrück" beträgt 10 Kilometer.
- Die geplante Verbindungsstraße wird als jene gerade Linie angesehen, die die beiden Punkte
"Zimtingen" und "Pfefferbrück" verbindet.
Beachten Sie, dass keine dieser Idealisierungen in der Wirklichkeit exakt erfüllt ist. Sie dienen
lediglich dazu, die gestellt Frage so abzuändern (oder "herzurichten"), dass sie von der Mathematik beantwortet werden
kann! Das auf diese Weise erhaltene mathematische Modell lässt sich leicht in einer Skizze wiedergeben:
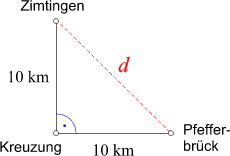
Von der ursprünglich geschilderten Situation sind nur mehr zwei Seiten eines Quadrats (der Seitenlänge 10 Kilometer)
übriggeblieben!
Die Frage nach der Länge einer direkten Verbindungsstraße reduziert sich auf die Frage, wie
lang die Diagonale des Quadrats ist. Diesem innermathematischen Problem sind wir ein Stück weiter
oben bereits begegnet. Die Antwort lautet: Die Länge der
Diagonalen ist 10√2 Kilometer oder, unter Ausnutzung der Dezimaldarstellung
(1) von √2,
d =
10√2 Kilometer =
14.1421356237309504880168872420969807856967... Kilometer.
|
|
|
(2) |
Das ist jetzt eine sehr genaue Angabe der Lösung! Die Aussage
"d = 10√2 Kilometer"
ist sogar eine exakte Lösungsangabe – allerdings ist sie
- nicht die Antwort auf die ursprüngliche Frage (Länge der Verbindungsstraße),
- sondern die Antwort auf die "übersetzte" Frage, die innerhalb des mathematischen Modells gestellt wurde
(Länge der Quadratdiagonale)!
Wie genau dürfen wir ihr trauen, wenn es um die Vorhersage der Länge der Verbindungsstraße geht?
Klarerweise ist die Antwort (2) gerade so zuverlässig wie
das mathematische Modell, aus dem sie gewonnen wurde! Je nachdem, wie genau die Angaben sind
(vor allem die Entfernungsangaben "10 Kilometer", aber auch die Annahme, die beiden Bundesstraßen
verlaufen geradlinig und schneiden einander in einem rechten Winkel), umso mehr Dezimalstellen von (2)
sind für das reale Problem von Bedeutung. Eine Lösungsangabe "14.142 Kilometer" wäre
immerhin auf einen Meter genau! Sind die Entfernungsangaben in der Straßenkarte auf ganze Kilometer gerundet (und
danach sieht es aus!), so mag es wohl ehrlicher sein, die Länge der Verbindungsstraße mit
"ungefähr 14 Kilometer" anzugeben. (Ist die Straße erst einmal gebaut, so wird sie in
der nächsten Auflage der Straßenkarte mit einer Länge von 14 Kilometern verzeichnet sein).
Um die Genauigkeit der Vorhersage zu erhöhen, müsste das Modell verbessert werden.
Beispielsweise könnte man die Entfernungen genauer als auf ganze Kilometer gerundet angeben.
(Dazu sollte man auch festlegen, wo genau die neue Straße die beiden Bundesstraßen
kreuzen soll und die Entfernungen auf diese Kreuzungspunkte beziehen. Entfernungen wären dann
immer zwischen Straßenkreuzungen angegeben. Die "Ortschaften" als solche wären
für das Modell irrelevant).
Das so erhaltene Modell wäre etwas komplizierter (es würde von der Diagonale eines
Rechtecks handeln, sofern die beiden gegebenen Abstände nicht genau gleich wären),
dafür aber zuverlässiger. Beispielsweise könnte es so aussehen:
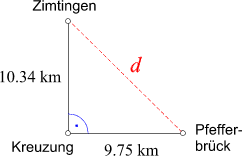
| | | |
| |
| | |
(Können Sie d berechnen?)
Weiteren Verbesserungsideen sind keine Grenzen gesetzt:
Vielleicht schneiden die beiden Bundesstraßen einander unter einem etwas anderen Winkel als 90°?
Ein derart verallgemeinertes Modell führt auf ein "trigonometrisches Problem",
das Sie mit den im Kapitel Trigonometrie besprochenen Techniken lösen können. Beispielsweise
könnte eine genauere Vermessung auf dieses Modell führen:
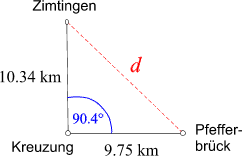
Vielleicht verlaufen die Bundesstraßen sogar leicht gekrümmt? Vielleicht kann die
geplante Verbindungsstraße wegen eines kleinen Hügels, der im Weg steht,
nicht wirklich geradlinig verlaufen? Dinge wie diese können nach Belieben
in mathematischen Modellen berücksichtigt werden, um ihre Relevanz für angewandte Fragestellungen
zu erhöhen. Je besser das Modell, umso besser das Resultat.
(In unserem Straßenbeispiel wird dem Verlangen nach genaueren Modellen irgendwann eine
natürliche Grenze gesetzt, denn die Länge einer Straße auf
Zentimetergenauigkeit zu kennen, wird für alle praktischen Zwecke wohl ausreichen...)
Anhand dieses Beispiels sollte klar geworden sein: Der Weg von einer praktischen Problemstellung
zu einer Formulierung, die die Anwendung mathematischer Techniken erlaubt, erfolgt über
Idealisierung und Modellierung. Ist ein mathematisches Modell gefunden,
das die Realsituation in den für die Fragestellung relevanten Zügen beschreibt, so sind die im Rahmen
dieses Modells von der Mathematik gegebenen Antworten gerade so glaubwürdig wie das Modell.
Oder, in einem kurzen Slogan zusammengefasst: Bei Anwendungen auf praktische
Problemstellungen ist die Mathematik gerade so perfekt wie das zugrunde gelegte Modell.
Mathematik funktioniert (fast) zu gut
| | | |

Trigonometrie
| |
| | |
Jedes mathematische Problem muss genau genommen nur ein einziges Mal durchdacht und gelöst werden.
Tritt das gleiche Problem wieder auf – vielleicht in einem anderen Zusammenhang –,
so ist es ja bereits gelöst! Tatsächlich wimmelt es in der Mathematik vor
kleineren und größeren Fragestellungen, deren Lösungen bekannt sind,
und die im Rahmen weitergehender Probleme immer wieder auftreten. Um einen – einmal gefundenen –
Lösungsweg in möglichst knapper Form festzuhalten und leicht kommunizierbar zu machen,
hat die Mathematik eine wirkungsvolle Methode erfunden: Formeln!
Beispiel: Betrachten wir noch einmal das Problem der Verbindungsstraße
zwischen Zimtingen und Pfefferbrück. Das mathematische Modell, das der letzten
der obigen Skizzen zugrunde liegt, geht davon aus, dass die beiden Bundesstraßen
geradlinig verlaufen, besteht aber im Unterschied zu allerersten Version nicht darauf,
dass sie einander unter einem exakt rechten Winkel schneiden und dass ihre Kreuzung von beiden
Ortschaften exakt gleich weit entfernt ist. Eine solche Situation ist hinreichend allgemein,
um öfters – mit unterschiedlichen Zahlenwerten, aber immer mit der gleichen mathematischen Struktur –
aufzutreten, beispielsweise in der Landvermessung. Auf den Punkt gebracht,
sieht die mathematische Struktur der Fragestellung so aus:
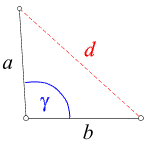
Gegeben sind die Längen a und
b sowie der Winkel
γ. Gesucht ist die Länge d.
Wie Sie sehen, wurden die Zahlen durch Symbole ersetzt. In jedem konkreten Anwendungsfall
erhalten sie wieder konkrete Zahlenwerte. Die Benennungen der Ortschaften und der Kreuzung sind
hinfällig. An ihre Stelle treten Punkte, die erst in einem konkreten Anwendungsfall wieder
eine besondere Bedeutung erhalten (etwa als Ortschaften, Kreuzungen, aber auch als markante Punkte in der
Landschaft wie alleinstehende Häuser oder Bäume).
Die Länge d zu ermitteln, wenn
a,
b und
γ bekannt sind,
ist ein trigonometrisches Standardproblem, dessen Lösung durch die Formel
|
|
|
__________________ |
| d
= |
√ |
a2 + b2 – 2 a b
cos γ |
|
(3) |
| | | |
| |
| | |
(den so genannten Cosinussatz) ausgedrückt wird.
Wenn Sie mit ihrem Mathematikstoff noch nicht bei den Winkelfunktionen
und der Trigonometrie angekommen sind, müssen Sie diese Formel nicht verstehen.
Für das, was wir Ihnen jetzt zeigen wollen, ist es sogar besser, wenn Sie sie nicht verstehen:
Mit ihrer Hilfe können Sie in jedem konkreten Anwendungsfall die Länge
d bestimmen, d.h.
das gestellte Problem lösen, ohne irgend etwas von der zugrundeliegenden Mathematik zu verstehen!
Dazu nehmen Sie einfach einen wissenschaftlichen Taschenrechner zur Hand. Er sollte die
Tasten √ oder
√x (Wurzelziehen),
x2 (Quadrieren) und
cos (was auch immer das ist) besitzen.
In jedem konkreten Anwendungsfall gehen Sie wie folgt vor:
| | | |

Cosinussatz
| |
| | |
- Geben Sie den Zahlenwert von a ein
- Drücken Sie auf die Taste x2
- Drücken Sie auf die Taste +
- Geben Sie den Zahlenwert von b ein
- Drücken Sie auf die Taste x2
- Drücken Sie auf die Taste –
- Geben Sie die Zahl 2 ein
- Drücken Sie auf die Taste ×
- Geben Sie den Zahlenwert von a ein
- Drücken Sie auf die Taste ×
- Geben Sie den Zahlenwert von b ein
- Drücken Sie auf die Taste ×
- Geben Sie den Zahlenwert von γ ein
- Drücken Sie auf die Taste cos
- Drücken Sie auf die Taste =
- Drücken Sie auf die Taste √
Die zuletzt angezeigte Zahl ist das Ergebnis, d.h. der gesuchte Zahlenwert von
d.
Anmerkung: Bei manchen Taschenrechnern
muss man zuerst eine Einstellung vornehmen, die die Verarbeitung von Winkeln regelt. Das Drücken der
Wurzeltaste √
ist auf manchen Taschenrechnern durch das Drücken der Taste
xy, gefolgt von der Eingabe 0.5, zu ersetzen, und wieder andere
Rechner verlangen eine ganz andere Eingabeart, aber in den meisten Fällen klappt's wie hier
angegeben.
Eine alternative Methode besteht darin, das Werkzeug "Online Rechnen mit Mathematica" mit dem
nebenstehenden Button aufzurufen, den Ausdruck
| | | |
Online Rechnen mit
| |
| | |
Sqrt[a^2 + b^2 - 2 a b Cos[γ*Pi/180.]]
in das Eingabefeld zu kopieren, die Symbole a, b
und γ durch ihre jeweiligen Zahlenwerte zu ersetzen
und auf "Ausführen" zu klicken.
Die obige Rechenanleitung im Stil eines Kochrezepts – man spricht auch von einem Algorithmus –
ist nichts anderes als eine (etwas umständliche)
Beschreibung der Formel (3). Wenn Sie einige mathematische Grundkenntnisse besitzen,
wird Ihnen vielleicht die Formel lieber sein als das Kochrezept,
aber im Grunde können beide dazu dienen, das gestellte Problem ohne Kenntnis der Trigonometrie
zu lösen. Ausgerüstet mit dieser Vorschrift (und vielleicht noch ein paar weiteren, die ähnliche
Probleme lösen) sowie einigen Messinstrumenten kämen Sie beispielsweise als
VermessungstechnikerIn ganz gut durch, ohne sich im Mindesten mit den mathematischen Grundlagen der
Landvermessung auskennen zu müssen!
Rechenanleitungen wie diese werden heute, wenn sie in Wissenschaft und Technik benötigt werden,
nicht in Form von Rezepten formuliert, sondern gleich als Ganzes an Computer übergeben.
In Eisenbahnzügen, Flugzeugen, MP3-Playern, aber auch im Thermometer mit Digitalanzeige, das
vielleicht bei Ihnen zu Hause an der Wand hängt und die Temperatur wahlweise in Grad Celsius oder in
Grad Fahrenheit anzeigt, werden ständig vorgefertigte Berechnungsschritte durchgeführt,
ohne dass uns das bewusst wäre.
(Früher wurden für solche Zwecke Tabellenwerke verwendet, denen man Zahlen entnehmen und
nach einem vorgegebenen Schema kombinieren musste. Auf diese Weise wurde etwa den Seeleuten
ein Zugang zur astronomischen Navigation ermöglicht, ohne dass diese mit der mathematischen
Grundlage – der sphärischen Trigonometrie – vertraut sein mussten).
| | | |

sphärische Trigonometrie
| |
| | |
Jede Formel, jede Rechenvorschrift hat ihre besondere Geschichte hinter sich:
Irgendwann wurde sie – oft nach eingehender Analyse des zugrundeliegenden
mathematischen Problems und einer Phase kreativen Nachdenkens – gefunden.
Mitunter waren Generationen von MathematikerInnen an einem solchen Prozess beteiligt.
In den Algorithmen und Computerprogrammen zur Lösung der verschiedensten
Probleme steckt also jede Menge mathematischen Wissens – aber es ist
in gewisser Weise ein eingefrorenes Wissen, ein Wissen, das nicht hier und
jetzt gewusst und gedacht werden muss, sondern das in nichts anderem mehr
besteht als einem funktionierenden Ablauf, der Erfüllung einer
bestimmten Aufgabe – ein Wissen, das als solches gar nicht mehr wahrgenommen wird!
Mit einem Wort: Mathematik hat eine gewisse Tendenz, sich in ihren eigenen Produkten
(Formeln, Verfahrensweisen) unsichtbar zu machen! Von diesem Standpunkt aus
betrachtet, funktioniert sie "zu gut" – sie gefährdet damit ihr
eigenes Image! Wenn die Rede auf die Mathematik kommt, denken wir nicht an Flugzeuge,
MP3-Player oder Digitaltermometer, sondern eher an die Rechenaufgaben aus dem
Mathematikunterricht
oder an mathematische Genies, deren Tun Normalsterblichen verschlossen bleibt.
Wozu Mathematik?
| | | |
| |
| | |
Hören wir jetzt eine Frage aufkommen?
Warum muss denn heutzutage überhaupt Mathematik verstanden werden,
wenn sie doch auch ohne Verständnis funktioniert und angewandt werden kann?
Wenn schon Mathematikunterricht – würde die Vermittlung vorgegebener
Verfahrensweisen nicht ausreichen? Das käme immerhin auch der Einstellung
"Ich will's nicht verstehen – ich möchte nur wissen, wie's geht!"
entgegen. Aus der Defensive heraus, in die wir uns jetzt hineingeredet haben,
seien einige Antworten erlaubt:
- Gerade in der heutigen Welt treten immer neue Problemstellungen auf, die noch nicht
in zufriedenstellender Weise in die Form mathematischer Modelle gebracht und gelöst wurden.
In vielen Berufen ist es nötig, mit einem gewissen Ausmaß an mathematischem Sachverstand
an die Formalisierung von Sachverhalten und Abläufen heranzugehen. (Beispiel: Der Komprimierung digitaler
Tonaufzeichnungen in das MP3-Format liegt ein neu entwickelter mathematischer Algorithmus zugrunde!)
- Wenn das in den Algorithmen eingefrorene Wissen nicht immer wieder "verflüssigt" wird,
wie soll es dann tradiert, d.h. an die jüngere Generation weitergegeben werden?
- Vielleicht sind Sie es gewohnt, beim Zahlen im Restaurant die "Rechnung" des Kellners
(in beiderlei Wortsinn) zu überprüfen. Zumindest könnten Sie es.
In ähnlicher Weise sollten wir etwa in der Lage ein, die Interpretation eines in den
Medien präsentierten statistischen Schaubildes – verständnisgeleitet –
zu überprüfen. Mathematisches Grundverständnis hilft, sich in vielen heute relevanten Fragen
eine eigene Meinung zu bilden.
- Mathematik ist eine kulturelle Errungenschaft. Sie ist die formale Basis eines modernen
wissenschaftlichen Weltbilds und hilft, unsere Kenntnis von der Welt (und zwar in so ziemlich
jedem Fachgebiet, dass Sie sich vorstellen können) zu vermehren.
Daher sollte ein gewissen Ausmaß an mathematischem Verständnis
Teil der Allgemeinbildung sein. Nebenbei bemerkt: Sie kann auch – ob Sie's glauben oder
nicht – Spaß machen!
- Und schließlich fällt die Erlernung von Verfahrensrezepten in der Regel leichter,
wenn die Mathematik, auf der sie beruhen, verstanden wurde. Ein bisschen plakativ könnte man sagen:
Viele praktische Anwendungen leiten sich aus (relativ) wenigen grundlegenden
mathematischen Tatsachen her.
Als Fazit ergibt sich, dass sowohl die Erlangung eines gewissen Grades an mathematischem
Grundverständnis als auch die Erlernung (und Einübung) mathematischer Verfahrensrezepte
wichtig sind.
|
| | |

Grafische Darstellung einer Häufigkeitsverteilung
| |
| | |
| | | |
Zum Seitenanfang | |
| | |
Wir wollen Sie nun in einem kleinen Streifzug auf das Erlernen mathematischer Ideen und Inhalte
einstimmen. Er versteht sich nicht als Übersicht über das Programm der
Mathematischen Hintergründe von mathe online,
sondern als eine Reihe wichtiger Hinweise auf ausgewählte Themen und Begriffe der
Mathematik.
Verborgene Muster
| | | |
| |
| | |
Mathematik hat – auch wenn viele Menschen das nicht glauben würden – viel mit Kreativität zu tun.
Es geht dabei um die Fähigkeit, formale Probleme so zu betrachten und zu beleuchten, dass
sich Lösungen anbieten, manchmal sogar "von selbst ergeben". Am klarsten tritt dieser Wesenszug der Mathematik
in spielerischen Denksportaufgaben zu Tage.
| | | |
| |
| | |
Beispiel: Die Geschichte vom Schachbrett und den Dominosteinen:
Rufen Sie mit dem nebenstehenden Link ein faszinierendes Rätsel auf (das Sie auch in der
Galerie unter Spielerisches finden)!
Eine andere Aufbereitung dieser Geschichte finden Sie unter
http://elearning.mat.univie.ac.at/spiele/esb/.
Auf den ersten Blick scheint das Problem sehr schwierig zu sein. Wenn Sie bis zur Lösung
vorgedrungen sind, werden Sie erkennen:
Es ist ein verborgenes Muster, eine verborgende Struktur (die zwar die ganze Zeit vorhanden war, aber
erst einmal erkannt werden will), die den Schlüssel zu einer verblüffend einfachen
Lösung darstellt. Diese Aufgabe ist in gewisser Weise typisch für die Mathematik:
So manches mathematische Problem galt lange Zeit als ungelöst – bis es jemand auf eine Art und Weise
betrachtete wie noch niemand zuvor und damit die Lösung fand!
| | | |
Schachbrett und Dominosteine
| |
| | |
Beispiel: Eine ähnlich gelagerte – wenngleich etwas komplexere – Aufgabe
ist das 14-15-Zahlenpuzzle, das Sie mit dem nebenstehenden Link aufrufen können
(und ebenfalls in der
Galerie unter Spielerisches finden).
Auch hier ist es eine auf den ersten Blick nicht einfach erkennbare Struktur
(der "Unordnungsparameter"), mit deren Hilfe sie sich lösen lässt.
In beiden Beispielen führt eine geeignete Betrachtungsweise zu einem
mathematischen Argument, mit dessen Hilfe die Lösung auch kommuniziert und von anderen
Personen nachvollzogen und verstanden werden kann.
Ein Argument zur Lösung eines offenen Problems zu finden, ist eine kreative Leistung.
Beides gehört zur Mathematik: das Finden und das – verständnisgeleitete – Nachvollziehen
eines Arguments.
Zahlen
| | | |
Das 14-15-Zahlen-
puzzle
| |
| | |
Zahlen sind in gewisser Weise die Atome der Mathematik.
Aufgrund ihrer überragenden Bedeutung werden sie
im Mathematikunterricht immer wieder und aus verschiedenen Blickwinkeln
beleuchtet.
Wir sind es in unserem Alltag gewohnt, mit
Ziffern, Bruchzahlen, negativen Zahlen und Zahlen in Dezimaldarstellung umzugehen,
so dass uns die Existenz dieser Objekte selbstverständlich erscheint.
Lassen Sie sich aber davon nicht täuschen! Der moderne – im Mathematikunterricht
vermittelte – Zahlbegriff wurde erst im 19. Jahrhundert geschaffen.
So lösten Fragen wie die nach der Länge der Quadratdiagonalen, der wir in (1)
bereits begegnet sind, vor zweitausend Jahren eine mathematische Grundlagenkrise aus!
Heute unterscheiden wir verschiedene Zahlentypen, und es stehen verschiedene Methoden, mit
Zahlen zu rechnen, zur Verfügung.
Das Rechnen mit Zahlen ist eines der Beispiele,
bei dem automatisierte Verfahrensweisen, die man "im Schlaf" anwenden können sollte,
nützlich sind (Stichwort Bruchrechnung!). Es gehört gewissermaßen
zum methodischen Handköfferchen, das man ständig mit sich tragen sollte.
Die arbeitssparendste Methode, diese Rechenregeln zu lernen und sie sich zu merken,
besteht darin, sie zunächst einmal zu verstehen. Üben verbessert und verfestigt dann
das Verstehen.
Buchstabenrechnen und Formeln
| | | |

Zahlen
| |
| | |
Ein bedeutender Schritt in der Entwicklung der Mathematik bestand darin,
Grössen, die in verschiedenen Zusammenhängen verschiedene Zahlenwerte
annehmen können, durch Buchstaben (bzw. allgemein durch Symbole) darzustellen.
Die dahinter liegende Logik ist nicht schwierig, auch wenn sie sich zu Beginn etwas
ungewohnt anfühlt.
Bei folgendem Beispiel begehen viele mit dem Buchstabenrechnen ungeübte Menschen einen
Fehler: Auf einem Universitätsinstitut gibt es p
Professoren und s Studierende.
Auf einen Professor kommen 6 Studierende. Drücken Sie die Beziehung zwischen
p und
s durch eine Formel aus!
Versuchen Sie's! Vielleicht ist ihr erster Tipp
Das wäre dann leider falsch! Macht nichts!
Der springende Punkt ist: Wie können Sie eigenständig überprüfen,
ob (4) die richtige Antwort ist oder nicht?
Dazu gibt es zwei Methoden. Versuchen Sie, beide zu verstehen:
- Methode 1 versucht, (4) "richtig zu lesen". Diese Formel besagt: Die
Zahl der Professoren ist 6 mal so groß wie die Zahl der Studierenden, was
offensichtlich nicht bedeutet, dass "auf einen Professor 6 Studierende kommen".
- Für Methode 2 ist ein Verständnis der
einfachen Idee, dass die verwendeten Symbole in einem konkreten Fall konkrete Zahlenwerte
annehmen, nützlich. Wir exerzieren sie langsam vor: Stellen Sie sich vor,
auf dem Institut gibt es 100 Studierende.
Das bedeutet, dass s durch
die Zahl 100 ersetzt wird:
s = 100.
Damit lautet (4) aber:
p = 6 · 100,
also
p = 600.
Wäre (4) richtig, so müsste es
600 Professoren geben, was
ebenfalls nicht bedeutet, dass "auf einen Professor 6 Studierende kommen".
Die richtige Lösung ist
Hier ergeben beide Methoden eine Bestätigung:
- Methode 1: Formel (5), richtig gelesen, lautet; Die
Zahl der Studierenden ist 6 mal so groß wie die Zahl der Professoren. Genau das
ist die Bedeutung der Aussage, dass "auf einen Professor 6 Studierende kommen".
- Methode 2: Angenommen,
auf dem Institut gibt es 100 Professoren.
Das bedeutet, dass p durch
die Zahl 100 ersetzt wird:
p = 100.
Damit lautet (5):
s = 6 · 100 = 600,
was ebenfalls passt.
Haben Sie verstanden, worum es geht? Sie können beide Methoden auch in vielen anderen Fällen
anwenden, wenn Sie sich nicht sicher sind, was eine Formel aussagt.
Funktionen
| | | |

Variable, Terme, Formeln und
Identitäten
| |
| | |
Besonders wichtig in allen Bereichen der Mathematik sind Situationen, in denen quantitative, d.h. durch Zahlen ausdrückbare
Beziehungen eine Rolle spielen. Eine Funktion
liegt – einfach ausgedrückt – vor,
wenn eine Größe von einer anderen Größe abhängt.
Stellen wir uns etwa vor, dass es eine ganze Reihe von Instituten unterschiedlicher
Größe gibt, wobei aber in jedem dieser Institute auf einen Professor 6 Studierende kommen.
Dann wird durch die Formel (5) eine Funktion beschrieben:
Ist p gegeben, so ist
s auch bekannt, nämlich
"6 mal so groß wie p".
Man sagt auch, s sei "eine
Funktion von p". Eine
häufig benutzte Schreibweise dafür ist
womit gemeint ist, dass s(p)
die Zahl der Studierenden an einem Institut mit
p Professoren ist.
An einem Institut mit 30 Professoren
gibt es daher
s(30) =
6 · 30 = 180
Studierende, an einem Institut mit 50 Professoren
gibt es
s(50) =
6 · 50 = 300
Studierende, an einem Institut mit 100 Professoren
gibt es
s(100) =
6 · 100 = 600
Studierende.
Weite Teile der Mathematik (und auch des Stoffs im Mathematikunterricht) handeln von Funktionen und ihren
Eigenschaften.
Obwohl viele der später betrachteten Funktionen durch kompliziertere Formeln als
(6) angegeben werden, ist das Grundprinzip, was eine Funktion
beschreibt, immer das gleiche: eine Größe, die von einer anderen abhängt.
Textaufgaben
| | | |

Funktionen 1
| |
| | |
Textaufgaben sind unbeliebt. Dennoch stellen Sie in gewisser Weise
die eigentliche Funktionsweise mathematischer Anwendungen dar.
Es gibt zwei Methoden, Textaufgaben zu lösen:
- Die empfohlene Methode: Denken Sie über die beschriebene Situation nach!
Was ist angegeben, was ist gefragt? Wird eine Alltagssituation beschrieben, unter
der Sie sich etwas vorstellen können? Wie lässt sich das in Worten gestellte Problem
mathematisch formulieren? Wie lässt es sich lösen?
Wenn Sie die Lösung haben: Was bedeutet sie?
Falls es sich um ein realistisches Anwendungsbeispiel handelt, dann versuchen Sie,
abzuschätzen, ob die mathematisch erhaltene Lösung
plausibel ist, z.B. ob die Größenordnung des Resultats stimmen kann!
- Die nicht empfohlene Methode: Sie erkennen einzelne Textstellen, die Sie an
vorhergegangene Textaufgaben erinnern, kombinieren die im Text enthaltenen Zahlen
in etwa so, wie es bei der früheren Aufgabe getan wurde (benutzen beispielsweise eine Formel,
die auch früher verwendet wurde) und hoffen, dass das Ergebnis richtig ist.
Die zweite Methode ist eine, die Sie vom Bemühen um Verständnis abbringt. Sie ignoriert, dass
Problemstellungen eine bestimmte Struktur haben, über die man Nachdenken kann,
und dass es einen Grund gibt, warum bestimmte Probleme auf bestimmte Weise gelöst
werden. Dass diese Methode Sie in die Irre führen kann,
illustriert das folgende (nicht ganz ernst gemeinte, aber dafür leicht durchschaubare) Beispiel:
Textaufgabe: Eine halbe Glatze hat 50 Haare. Wie viele Haare hat eine ganze Glatze?
Methode 2 könnte Sie dazu verleiten, die Regeln der Schlussrechnung (des Dreisatzes) anzuwenden und
als Lösung 100 zu vermuten – was klarerweise Unsinn ist.
Ein bisschen weniger offensichlich ist der Fallstrick bei der folgenden Aufgabe:
Textaufgabe: Eine Brille mit 2 Dioptrien kostet 30 Euro. Wieviel kostet eine Brille
mit 3 Dioptrien?
Bitte sagen Sie nicht, dass die Antwort 45 Euro lautet!
Textaufgaben werden im Unterricht nicht nur eingesetzt, um formale und abstrakte mathematische
Operationen an konkrete Anwendungen zu knüpfen, sondern auch, um Sie Erfahrungen mit
dem eigenständigen Überlegen und dem mathematischen Modellieren machen zu lassen.
Daher kann es immer passieren, dass in eine Textaufgabe kleine Gemeinheiten eingebaut sind.
Textaufgabe: Die Städte A
und B sind
45 Kilometer voneinander entfernt. An einem schönen Frühlingstag herrscht eine
Temperatur von 22 Grad Celsius. Ein Zug fährt mit einer Geschwindigkeit von
90 Kilometer pro Stunde von A
nach B. Wie lange dauert die
Reise?
Bei diesem Beispiel sollte Ihnen klar sein,
dass die Angabe "22 Grad Celsius" für die Beantwortung der Frage irrelevant ist.
Ignorieren Sie sie einfach!
Lösen Sie die Aufgabe selbst! (Sie brauchen dafür nicht einmal etwas
aufzuschreiben). Klarerweise werden hier (auch wenn üblicherweise nicht von Ihnen
verlangt wird, das im Lösungsweg eigens anzugeben) einige Idealisierungen vorgenommen,
nämlich, dass die Städte A
und B als
Punkte behandelt werden, dass der Zug immer mit genau der gleichen angegebenen
Geschwindigkeit fährt (was zumindest beim Abfahren und Ankommen in der Realität nicht der
Fall ist) und dass die Länge des Zuges vernachlässigt wird.
Textaufgaben dieser Art sind insofern realistisch, als die Auswahl der zu verwendeten
Daten in der Praxis ein wichtiger Teil des Modellierungsprozesses ist.
Lassen Sie uns noch ein paar Worte zum Vorgang der Modellierung (der ja mit den meisten Textaufgaben
verbunden ist) sagen. Hier ist es in konkreten Fällen wichtig, sich zu fragen, ob und
in welcher Weise die zur Verfügung stehenden mathematischen Strukturen und Methoden
auf ein bestimmtes Problem angewandt werden können (bzw. dürfen).
Gerade in dieser Hinsicht sitzen wir immer wieder Missverständnissen auf.
Frage: Ist eine Temperatur von 20 Grad Celsius doppelt so warm als eine Temperatur
von 10 Grad Celsius?
Man wäre vielleicht versucht, die Frage mit "ja" zu beantworten.
In manchen Ländern wird die Temperatur aber in Grad Fahrenheit gemessen.
Auf der Seite
Umrechnung Temperatur
(von Jumk.de)
können Sie selbst Temperaturangaben zwischen Celsius und Fahrenheit umrechnen.
Nun betrachten Sie folgende Umrechnungstabelle:
|
Grad Celsiuis
|
Grad Fahrenheit
|
|
10
|
50
|
|
20
|
68
|
Wenn eine Temperatur von 20 Grad Celsius tatsächlich doppelt so warm wäre als
eine Temperatur von 10 Grad Celsius, so müsste das unabhängig vom
System, Temperaturen anzugeben, gelten. Das ist aber hier nicht der Fall,
denn 68 ist nicht das Doppelte von 50! Die Antwort ist daher ein klares "Nein".
Wieder haben wir es hier mit einer Frage zu tun, die – etwas subtiler als in den Beispielen mit der
Glatze und der Brille – durch ihre Formulierung die Anwendung
einer mathematische Struktur suggeriert, die in diesem Zusammenhang einfach nicht anwendbar ist.
Fazit: Bei Textaufgaben immer mitdenken!
Geometrie
| | | |
zur Temperatur
| |
| | |
Geometrie ist ein Teilgebiet der Mathematik, das auf den ersten Blick nichts mit Zahlen, Formeln und
Buchstabenrechnen zu tun hat, sondern mit Strecken, Winkeln und Figuren.
Wie so oft trügt auch hier der Schein: Zu den bedeutendsten Entwicklungen der
Mathematik in der Neuzeug zählt die "Algebraisierung der Geometrie".
Die Bezeichnung Algebra bezieht sich dabei auf den Bereich der Zahlen, Formeln und
des Buchstabenrechnens.
Der moderne Zugang zur Geometrie ist, ein bisschen vereinfacht gesagt, nicht ein
zeichnerisch-anschaulicher, sondern ein rechnerischer-abstrakter. Um den Unterschied
zu verdeutlichen, hier zwei Formulierungen, was ein Kreis ist:
|
Der Kreis mit Mittelpunkt M
und Radius r
ist die Menge aller Punkte der Ebene, die vom Punkt
M
den Abstand r besitzen.
|
Der Kreis mit Mittelpunkt
(mx, my)
und Radius r
ist die Menge aller Zahlenpaare
(x, y), für die
(x – mx)2 + (y – my)2
= r2
gilt.
|
| | | |
| |
| | |
Die erste ist eine anschauliche Formulierung, die direkt in eine Zeichnung umgemünzt werden kann.
Die zweite (die wir hier nur zur Illustration wiedergeben – Sie müssen sie jetzt
nicht verstehen, wenn die "analytische Geometrie" noch nicht zu Ihrem Stoff
gehört) entspricht dem modernen Zugang: sie beschreibt – obwohl man ihr das nicht
sofort ansieht – die gleiche mathematische Idee, aber auf eine formalere Weise.
| | | |

Analytische
Geometrie 1 |
2 |
3 (in Vorbereitung)
| |
| | |
Der Vorteil des modernen Zugangs besteht darin, dass er weitreichender und mächtiger ist
als der ältere. Begriffe wie Geraden- und Ebenengleichungen, Kreis- und Kugelgleichungen,
Anstieg, Vektoren, Skalarprodukt und Vektorprodukt
gehören in diesen Teil der Mathematik.
Bei ihm ist es wichtig, sich vor Augen zu halten, dass trotz der Abstraktheit des
Formalismus letzten Endes geometrisch-anschauliche Dinge gemeint sind.
Symmetrien
| | | |

Vektoren 1 |
2
| |
| | |
In vielen Bereichen der Mathematik ist es nützlich, Symmetrien zu erkennen und aus ihrer
Existenz Erkenntnisse zu gewinnen. Da gibt es einerseits die geometrischen Symmetrien
von Figuren und Körpern.
| | | |
| |
| | |
Ein schönes Beispiel ist die Aufgabe mit dem Bild im Spiegel, die Sie mit dem nebenstehenden
Link aufrufen können. Sehen Sie sich an, wie sie gelöst wird!
Die
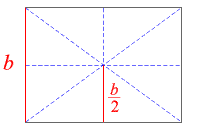 Symmetrie, um die es hier geht, wird offenbar, wenn wir uns das zentrale geometrische Argument
ansehen, das dabei verwendet wird: Der Schnittpunkt der Diagonalen eines
Rechtecks liegt genau in dessen Mitte: Werden, wie in der nebenstehenden Skizze gezeigt, die
beiden Diagonalen eines Rechtecks gezogen und danach die zu den Seiten parallelen Strecken durch
den Schnittpunkt der Diagonalen, so ist die in roter Farbe
dargestellte Strecke vom Diagonalenschnittpunkt zur unteren Rechtecksseite genau
genau halb so groß wie die ebenfalls in roter Farbe dargestellte
Seitenlänge b.
Dieses Argument wird im Spiegel-Applet auf zwei Rechtecke angewandt.
Aber wieso gilt es eigentlich? Seine Richtigkeit scheint sonnenklar zu sein.
Der Grund für die Sicherheit, mit der wir es benutzen, liegt darin, dass in dieser
Situation eine Symmetrie vorliegt: Die obere und die untere Hälfte des Rechtecks
sind gewissermaßen "gleichberechtigt". Führen Sie die Maus über die
Grafik! Dann wird (in grüner Farbe) eine weitere Strecke eingeblendet,
die aufgrund der Symmetrie genauso lang sein muss wie die kurze rote Strecke,
und daher halb so lang wie die lange rote Strecke.
Symmetrie, um die es hier geht, wird offenbar, wenn wir uns das zentrale geometrische Argument
ansehen, das dabei verwendet wird: Der Schnittpunkt der Diagonalen eines
Rechtecks liegt genau in dessen Mitte: Werden, wie in der nebenstehenden Skizze gezeigt, die
beiden Diagonalen eines Rechtecks gezogen und danach die zu den Seiten parallelen Strecken durch
den Schnittpunkt der Diagonalen, so ist die in roter Farbe
dargestellte Strecke vom Diagonalenschnittpunkt zur unteren Rechtecksseite genau
genau halb so groß wie die ebenfalls in roter Farbe dargestellte
Seitenlänge b.
Dieses Argument wird im Spiegel-Applet auf zwei Rechtecke angewandt.
Aber wieso gilt es eigentlich? Seine Richtigkeit scheint sonnenklar zu sein.
Der Grund für die Sicherheit, mit der wir es benutzen, liegt darin, dass in dieser
Situation eine Symmetrie vorliegt: Die obere und die untere Hälfte des Rechtecks
sind gewissermaßen "gleichberechtigt". Führen Sie die Maus über die
Grafik! Dann wird (in grüner Farbe) eine weitere Strecke eingeblendet,
die aufgrund der Symmetrie genauso lang sein muss wie die kurze rote Strecke,
und daher halb so lang wie die lange rote Strecke.
Ganz allgemein spricht man in der Mathematik von einer Symmetrie, wenn eine derartige Form von
"Gleichberechtigung" vorliegt.
Ein ganz anderes Beispiel: Wie groß ist die Wahrscheinlichkeit, mit einem (fairen) Würfel
die Augenzahl 6 zu erzielen? Das wissen Sie natürlich: sie ist ein Sechstel. Das bedeutet,
dass unter sehr vielen Würfen bei etwa einem Sechstel die Augenzahl 6 auftritt. Je
größer die Zahl der Würfe ist, umso genauer gilt diese Aussage. Aber wieso
gilt sie? Auch hier ist eine Symmetrie im Spiel: alle Augenzahlen sind "gleichberechtigt" (sonst
wäre der Würfel nicht fair). Wenn alle 6 Augenzahlen gleich oft vorkommen, so muss
aufgrund der Symmetrie jede einzelne Augenzahl bei einem Sechstel aller Würfe
auftreten.
Überlegen Sie selbst, mit welchem Symmetrieargument Sie die Winkel in einem gleichseitigen
Dreieck ermitteln können!
Das Unendliche
| | | |
Applet
Das Bild im Spiegel
| |
| | |
Mit fortschreitendem Mathematikstoff kommt ein Thema ins Blickfeld, das wie kein anderes die moderne Mathematik
prägt: das "Unendliche". Was ist das eigentlich? Keine Zahl ist "unendlich groß".
Kein Rechenschritt kann buchstäblich "unendlich oft" durchgeführt werden.
Man kann zwar sagen, dass es unendlich viele Zahlen gibt, aber niemand kann unendlich viele
Zahlen aufzählen oder hinschreiben. Zwei Zahlen können gleich sein, aber sie können
nicht "unendlich nahe beieinander liegen".
Die moderne Mathematik hat dennoch Wege gefunden, mit der Idee des Unendlichen umzugehen.
Das "unendlich Große" wird in der Regel als Gegenteil des "Endlichen" aufgefasst.
Da die "Anzahl aller Zahlen" selbst keine Zahl (und damit eigentlich ein sinnloses Konstrukt) ist,
wird gesagt, dass es unendlich viele Zahlen gibt. Das eigentlich faszinierende Thema ist aber
das "unendlich Kleine". Es stellt sich beispielsweise, wenn wird uns vorstellen, eine Kurve
in der Nähe eines ihrer Punkte "mit einer Lupe anzusehen", unser Blickfeld also
"heranzuzoomen". Wird die Lupe immer stärker, so wird die Kurve (wir stellen uns eine
Kurve ohne Knicke und Ecken vor) immer "gerader" aussehen. Und wenn die Lupe "unendlich
stark wäre", also ein "unendlich kurzes Kurvenstück" zeigen würde? Eine solche
Lupe gibt es natürlich nicht, aber wir können uns eine Abfolge immer stärkerer Lupen
vorstellen, deren Abbilder sich einer bestimmten geraden Linie beliebig nahe annähern
– und mit dieser geraden Linie haben wir herausgefunden, wie die Kurve in einer
unendlich starken Lupe aussehen würde! Dieser "Grenzübergang" – der auch
rechnerisch bewerkstelligt werden kann – führt direkt zu
einem der mächtigsten Instrumente der Mathematik: der Differentialrechnung und in der Folge
zur Integralrechnung.
| | | |

Differenzieren 1 |
2

Integrieren
| |
| | |
Als Symbol für "Unendlich" wird in der Mathematik einheitlich das Zeichen
∞
verwendet.
Definitionen
| | | |
| |
| | |
Vor Definitionen müssen Sie sich am allerwenigsten fürchten!
Eine Definition ist lediglich eine Namensgebung. Definitionen dienen dazu,
eine Sprache zu entwickeln, die mathematische Sachverhalte so ausdrücken kann,
dass wir alle das Gleiche meinen und nicht aneinander vorbeireden.
Die Wörter, die dabei verwendet werden, sind oft der Alltagssprache entlehnt.
Um ein Beispiel anzugeben, gehen wir vom Begriff der ganzen Zahlen aus.
Es sind dies die Zahlen ...–4, –3, –2, –1, 0 1, 2, 3, 4,...
Werden zwei ganze Zahlen miteinander multipliziert, so ist das Ergebnis wieder eine ganze Zahl.
Beispiele dafür sind: 2 · 3 = 6, (–2) · 3 = –6
und (–2) · (–3) = 6. Nun zu unserem Beispiel:
Definition 1: Eine gerade Zahl ist
eine ganze Zahl, die die Eigenschaft hat, das Doppelte einer ganzen Zahl zu sein.
Nach dieser Definition sind die geraden Zahlen genau diese:
...–8, –6, –4, –2, 0 2, 4, 6, 8,...
Theoretisch könnte man ganz beliebige Definitionen formulieren. Hier ein weiteres Beispiel:
Definition 2:
Eine Daisy-Duck-Zahl ist eine ganze Zahl, die größer
als 72 und kleiner als 99 ist.
Nach dieser Definition ist 75 eine Daisy-Duck-Zahl, 123 aber nicht.
Das wäre allerdings eine Definition, die mathematisch nicht besonders interessant ist,
und kaum jemand würde sie (wofür auch?) aufgreifen und verwenden wollen. Definitionen
sind sinnvoll, wenn sie etwas mathematisch Interessantes bezeichnen, etwa einer
beachtenswerten Struktur einen Namen geben.
In Definitionen können zuvor definierte Begriffe verwendet werden:
Definition 3: Eine ungerade Zahl ist eine ganze Zahl, die keine gerade Zahl ist.
Begriffe, die sorgfältig definiert wurden, können benutzt werden, um
mathematische Aussagen zu treffen. Für die Begriffe "gerade Zahl" und "ungerade Zahl"
gelten beispielsweise die folgenden Aussagen:
- Jede ganze Zahl ist entweder gerade oder ungerade.
- Von zwei benachbarten ganzen Zahlen ist immer eine gerade und eine ungerade.
- Das Produkt einer geraden mit einer ungeraden Zahl ist gerade. (Diese Aussage werden wir im
nächsten Unterabsschnitt beweisen).
- Das Produkt zweier benachbarter ganzer Zahlen ist gerade. (Diese Aussage werden wir im
nächsten Unterabsschnitt beweisen).
Bei Definitionen kommt es darauf an, sie genau zu lesen! Um es an einem Beispiel zu verdeutlichen:
Ist die Zahl 4.4 eine gerade Zahl?
Vielleicht sieht es so aus, denn 4 ist eine gerade Zahl. Aber in Definition 1
heißt es "Eine gerade Zahl ist eine ganze Zahl...", und 4.4 ist keine ganze Zahl.
Daher ist 4.4 keine gerade Zahl.
Argumentieren und beweisen
| | | |
| |
| | |
Mathematische Aussagen (so genannte Sätze oder Theoreme) sind nicht immer offensichtlich – in der Regel müssen wir (mehr oder weniger)
Aufwand betreiben, um uns ihrer Richtigkeit zu versichern, d.h. sie zu beweisen.
Ob Beweise unter Zuhilfenahme von Symbolen oder rein verbal geführt werden,
ist eine Frage der Zweckmäßigkeit.
Hier ein Beispiel für einen Beweis, der Symbole benutzt:
Satz 1: Das Produkt einer geraden mit einer ungeraden Zahl ist gerade.
Beweis: Die gerade Zahl sei mit
g bezeichnet, die
ungerade mit u. Der
Beweis wird in drei Schritten geführt:
- Da g gerade ist und
eine gerade Zahl das Doppelte einer ganzen Zahl ist, können wir
g in der Form
g = 2 k
schreiben, wobei k
eine ganze Zahl ist.
- Daher ist
g u =
2 k u, was genau das Doppelte der ganzen Zahl
k u
ist.
- Folglich ist das Produkt g u
eine gerade Zahl.
Die farblichen Hervorhebungen helfen Ihnen vielleicht, die Struktur des Arguments zu verstehen.
Ein Beispiel für einen rein verbal geführten Beweis ist das folgende:
Satz 2: Das Produkt zweier benachbarter ganzer Zahlen ist gerade.
Beweis: Von zwei benachbarten Zahlen ist immer eine gerade und eine ungerade.
Da das Produkt einer geraden mit einer ungeraden Zahl gemäß Satz 1
gerade ist, ist das Produkt zweier benachbarter ganzer Zahlen gerade.
| | | |
| |
| | |
Den genauen Regeln des mathematischen Argumentierens (der mathematischen Logik) – die selbst auf mathematische Weise
formuliert werden können – ist ein eigenes Kapitel gewidmet.
Hier wollen wir nur auf zwei häufig anzutreffende Typen von Situationen
und die für sie benutzten Schreibweisen hinweisen.
Beim mathematischen Argumentieren müssen oft Aussagen aus anderen Aussagen gewonnen werden.
Beispielsweise folgt aus der Aussage "Heute regnet es" die Aussage "Es ist sinnvoll,
einen Regenschirm mitzunehmen". Wenn wir auf diese Weise von einer Aussage auf eine andere
schließen, verwenden wir das Symbol
=>
(oder Þ),
auszusprechen als "daraus folgt".
Beispiel: n ist eine ganze Zahl
=>
n(n + 1) ist eine gerade Zahl
Man kann das auch so lesen: "Wenn n eine ganze Zahl ist, so folgt,
dass n(n + 1) eine gerade Zahl ist".
Überprüfung anhand eines Beispiels:
5 ist eine ganze Zahl, 5 · 6 = 30 ist eine gerade Zahl.
Manchmal ist es nötig, mit verschiedenen Formulierungen ein und desselben mathematischen
Sachverhalts zu operieren, d.h. mit gleichwertigen Aussagen.
Gilt eine von zwei gleichwertigen Aussagen, so gilt auch die andere.
Das Symbol, das in diesen Fällen benutzt wird, ist
<=>
(oder Û),
auszusprechen als "genau dann, wenn".
Beispiel: n ist das
Doppelte einer ganzen Zahl
<=>
n kann ohne Rest
durch 2 dividiert werden.
Man kann das auch so lesen: "Die Zahl n ist genau dann
das Doppelte einer ganzen Zahl, wenn sie ohne Rest durch 2 dividiert werden kann".
Die Verwendung der Symbole =>
und <=> kann also jederzeit durch eine
verbale Formulierung ersetzt werden. Womit wir bei einem anderen wichtigen Thema wären: der Formulierung mathematischer
Sachverhalte in Worten.
Die Rolle der Sprache in der Mathematik
| | | |

Exaktheit und Logik
| |
| | |
Mathematik wird zwar selbst oft als Sprache bezeichnet, man spricht auch von "mathematischer Sprache",
aber nun wollen wir uns kurz der gesprochenen Sprache zuwenden, d.h. der Alltagssprache,
einigermaßen präzise eingesetzt und hie und da mit Fachvokabeln angereichert.
Mathematische Sachverhalte können oft rein verbal dargestellt werden, und bis zur
Entwicklung des umfassenden Apparats an mathematischen Symbolen, der heute zur Verfügung steht,
mussten auch MathematikerInnen ihre Argumentationen und Ergebnisse entweder in
grafischer Form – durch Skizzen – oder in Worten darstellen.
In vielen Fällen stellt die Verwendung mathematischer Symbole (Buchstaben) eine
Erleichterung dar. Wir sind oben darauf eingegangen.
Dennoch ist es oft nützlich, den durch eine Formel ausgedrückten Sachverhalt
in Worten zu formulieren. Insbesondere hilft es – sowohl Lernenden als auch
Menschen, die beruflich Mathematik betreiben – beim Verstehen. Es hilft, die
eigenen Gedanken zu ordnen, das eigene Verständnis zu überprüfen, und
schließlich hilft es, sich mathematische Inhalte besser zu merken.
Scheuen Sie sich nicht davor, auch wenn es zu Beginn schwierig ist!
Albert Einstein hat einmal gemeint, was man wirklich verstanden hat, könne man auch seiner
Großmutter erklären, und das Sprechen über Mathematik und mathematische
Operationen geht ein bisschen in diese Richtung.
Beispiel: Die Gleichung
x2 = x + 6
kann in Worten so beschrieben werden: "Ich bin interessiert an einer Zahl, die die folgende
Eigenschaft hat: Quadriere ich sie, so erhalte ich das gleiche Ergebnis als wenn ich 6 zu ihr addiere".
(Können Sie so eine Zahl finden? Tatsächlich gibt es zwei derartige Zahlen!)
Dieser verbale Beschreibung besitzt zwei Vorteile:
- Sie stellen (vor sich selbst) sicher, zu wissen, was eine Gleichung ist.
- Sie legen die mathematische Struktur dieser Gleichung offen. Klarerweise kann die Gleichung
u2 = u + 6,
die ja ein bisschen anders aussieht als die obige, in der gleichen Weise verbal beschrieben werden.
Es handelt sich also – trotz der Verschiedenheit der benutzten Symbole – um
dieselbe Gleichung!
Das Verstehen mathematischer Inhalte kann auch in geschriebenen Worten dokumentiert werden,
beispielsweise in einer schriftlichen Prüfungsarbeit. So empfiehlt es sich beispielsweise,
bei der Lösung von Aufgaben durchaus die eine oder andere erklärende Bemerkung
einzufügen und das Ergebnis nicht nur brav zu unterstreichen, sondern – etwa, wenn
es sich um eine Textaufgabe handelt – auch als verbale Antwort auf die gestellte Frage
zu formulieren.
Wie eindeutig sind mathematische Lösungswege?
| | | |
| |
| | |
Für viele Menschen ist es ein Gräuel, zu erfahren, dass mathematische Probleme nicht immer nur
auf eine einzige Weise gelöst werden können. Hier ein Beispiel, das Sie allerdings nur verstehen
werden, wenn Sie schon mit Termen, quadratischen Gleichungen und der Darstellung von Parabeln als
Funktionsgraphen vertraut sind. (Ansonsten überspringen Sie es einfach!)
Beispiel: Es ist zu zeigen, dass die quadratische Gleichung x2 = 1
genau zwei reelle Lösungen besitzt.
- Lösungsweg 1: Die gegebene Gleichung kann auch in der Form
x2 –1 = 0
geschrieben werden. Die linke Seite ist identisch mit
(x – 1)(x + 1),
ist also ein Produkt. Ein Produkt aus zwei Zahlen kann nur dann gleich
0 sein, wenn einer der beiden Faktoren
gleich 0 ist. Daraus folgt, dass entweder
x – 1 = 0
(und daher x = 1)
oder
x + 1 = 0
(und daher x = –1)
ist. Mehr als diese zwei (reellen) Lösungen kann es nicht geben.
- Lösungsweg 2: Um die gegebene Gleichung zu lösen, kann die so genannte "kleine Lösungsformel"
benutzt werden. Aus ihr ergeben sich unmittelbar die beiden reellen
Lösungen x = 1
und
x = –1.
- Lösungsweg 3: Der Graph der durch
f(x) = x2 – 1
definierten Funktion f
ist eine nach oben offene Parabel, deren Scheitelpunkt die
y-Koordinate
f(0) = –1 besitzt,
also unterhalb der y-Achse liegt.
Die Funktion f hat daher
genau zwei Nullstellen, die den beiden reellen Lösungen der gegebenen Gleichung entsprechen.
| | | |

kleine Lösungsformel

Graph |
Nullstelle
| |
| | |
Aber – seien Sie ehrlich! – dass es mehrere Wege gibt, um ein Problem zu lösen, ist eigentlich
gar nicht nicht verwunderlich. Wie kommen Sie
in einer Stadt, die Sie gut kennen, von A
nach B (beispielsweise vom
Rathaus zum Hauptbahnhof)? Vielleicht gibt es einen kürzesten Weg, aber tatsächlich
wird es viele Wege geben, die in Frage kommen. Ein Neuankömmling
wird vielleicht eine andere Route einschlagen als ihren Lieblingsweg und dennoch ans Ziel kommen.
Und in der Mathematik sind oder waren wir alle Neuankömmlinge!
Verschiedene Wege in Gedanken auszuprobieren kann nicht nur dazu dienen, eine Stadt besser
kennen zu lernen, sondern auch die Mathematik.
Dass es für ein und dasselbe mathematische Problem verschiedene Lösungswege geben kann,
illustriert einen besonderen Zug der Mathematik:
Sie ist nicht eine unzusammenhängende Sammlung von Methoden,
jede fein säuberlich für ein bestimmtes Problem entworfen,
sondern stellt eher ein logisches Geflecht dar.
Ein bisschen nach dem Motto "Alles hängt mit Allem zusammen".
Freunden Sie sich daher mit der Mehrdeutigkeit mathematischer Problemlösungsstrategien an!
Schlimmer noch: Freunden Sie sich damit an, dass auch das Ergebnis nicht immer
haargenau das Gleiche ist!
Beispiel: Wie lange ist die Diagonale eines quadratische Platzes mit 100 Meter Seitenlänge?
Die Sache mit der Quadratdiagonalen haben wir oben bereits besprochen.
Wie auch immer sie berechnet wird, verschiedene Lösungsangaben sind möglich:
- Die Länge der Diagonale des Platzes beträgt 100√2 Meter.
- Die Diagonale des Platzes ist √2 mal so lang wie die Seitenlänge.
- Die Länge der Diagonale des Platzes beträgt 141.42135623730950... Meter.
- Die Länge der Diagonale des Platzes beträgt 141 Meter, 42 Zentimeter und 1 Millimeter.
- Die Länge der Diagonale des Platzes beträgt 141.42 Meter.
- Die Länge der Diagonale des Platzes beträgt 141.4 Meter.
- Die Länge der Diagonale des Platzes beträgt 141 Meter.
Alle diese Lösungsangaben haben ihre Berechtigung.
Die ersten beiden sind exakt, wenngleich sie sich nicht auf einen realen, sondern auf einen
mathematisch idealisierten Platz beziehen. Die dritte gibt die Länge
genauer an als die Größe eines Atoms und deutet durch die Punkte an, dass es
noch genauer ginge. Die verbleibenden vier haben alle eine bestimmte Genauigkeit gewählt.
(Welche Möglichkeiten sinnvoll sind, hängt davon ab, wofür man
die Länge der Diagonale wissen möchte. Das wird hier nicht dazugesagt.
Es könnte sich um die Anlage eines Weges oder um ein physikalisches Präzisionsexperiment
handeln. Auch wenn der Zweck bekannt ist, besteht noch einige Freiheit, den
Lösungswert zu runden – eine Spur genauer als nötig kann nicht schaden,
aber damit zu übertreiben, macht keinen Sinn!)
Dass eine gewisse Freiheit bei der Wahl des Lösungsweges und bei der Formulierung von
Antworten auf angewandte Fragen besteht, unterstreicht, dass Kreativität
in der Mathematik eine wichtige Rolle spielt.
Euklid und Hilbert
| | | |
| |
| | |
Jetzt wollen wir noch einen kurzen Blick auf die Struktur mathematischer Argumentation werfen,
wie sie professionell, d.h. im Rahmen der Mathematik als Wissenschaft betrieben wird.
Methodisch gesehen will Mathematik die Wahrheit gewisser Aussagen sicherstellen.
Dazu ist es nötig, genau zu wissen, wovon man ausgehen darf und wie man
von diesen Ausgangspunkten weitergeht. Die grundsätzliche Vorgangsweise
wurde bereits vor mehr als zweitausend Jahren von Euklid von Alexandria für die
Geometrie formuliert:
- Ausgangspunkt sind die so genannten Axiome.
Für Euklid waren das Aussagen, deren Gültigkeit nicht bezweifelt werden können.
Heute bezeichnet man mit diesem Begriff schlicht die Grundsätze, die an den
Anfang gestellt werden, und die zunächst als wahr angenommemn werden.
Diese Vorgangsweise ist heute in der gesamten Mathematik gebräuchlich.
Die verwendeten Axiome sind zum Teil so abstrakt, dass die Formulierung
"deren Gültigkeit nicht bezweifelt werden können" auf sie nicht mehr wirklich
zutrifft.
Es gilt lediglich der Grundsatz, dass die verwendeten Axiome einander nicht widersprechen
dürfen.
- Ausgehend von den Axiomen werden durch logisches Schließen Folgerungen gewonnen,
die mathematischen Sätze (Theoreme).
Im frühen 20. Jahrhundert formulierte der Mathematiker David Hilbert eine
Zukunftsvision für die Mathematik, die darauf hinauslief, ausgehend von einigen Axiomen
jede mathematische Wahrheit erschließen zu können.
In heutigen Begriffen ausgedrückt, würde das bedeuten,
alle mathematischen Wahrheiten von einem Computerprogramm, das mit den Regeln des logischen
Schließens gefüttert wurde, erzeugen zu lassen (und daher auch die Entscheidung, ob eine
gegebene mathematische Aussage wahr ist oder nicht, einem Programm überantworten
zu können). Die Grundlage für die Hoffnung, dass das – zumindest im Prinzip –
möglich ist, ist die Annahme, dass der Bereich der mathematischen Wahrheit
in gewissem Sinn "objektiv" und unabhängig von den Menschen existiert.
Das würde auch bedeuten, dass jede anständig formulierte mathematische
Aussage (etwa: "Es gibt eine gerade Zahl, die größer als 4 und nicht die Summe zweier
Primzahlen ist" – ein berühmtes, bis heute ungelöstes Problem)
entweder war oder falsch ist, und dass es einen Weg gibt, sie aus den
Axiomen, die das Rechnen mit Zahlen begründen, zu beweisen oder zu widerlegen.
Gödel
| | | |
| |
| | |
Im Jahr 1931 entdeckte der österreichische Mathematiker Kurt Gödel,
dass Hilberts Vision nicht eingelöst werden kann!
Mit seinem "Unvollständigkeitssatz" stürzte er die Mathematik
in eine Grundlagenkrise: Legt man sich auf ein System von endlich vielen Axiomen
(das zumindest so reichhaltig ist, dass damit das
Rechnen mit den natürlichen Zahlen begründet werden kann) fest, so gibt es immer Aussagen,
die auf der Basis der verwendeten Axiome weder bewiesen noch widerlegt werden können.
Um sie beweisen oder widerlegen zu können, ist eine Erweiterung des
Axiomensystems nötig.
In manchen Fällen kann man sich die Wahrheit oder Unwahrheit einer solchen Ausage
sogar aussuchen (indem man entweder sie oder ihr Gegenteil den verwendeten Axiomen als weiteres Axiom
hinzufügt)!
Jedes (hinreichend reichhaltige) Axiomensystem ist in diesem Sinn unvollständig.
Mathematische Wahrheit ist nicht hundertprozentig "objektiv", sondern hängt in einem gewissem Ausmaß
von den verwendeten Axiomen ab – und damit von menschlichen Konventionen!
Es verwundert wohl nicht, zu hören, dass diese fundamentale Erkenntnis mit dem Problem
des "Unendlichen" zu tun hat. Mittlerweile hat sich die Mathematik von
ihrem Schock erholt und die Erforschung der
genauen Art ihrer Abhängigkeit von Konventionen zu einer eigenen
Fachrichtung gemacht, die dem Bereich der mathematischen Logik zugerechnet wird.
Mathematik ist also weder lediglich "Rechnen" noch eine Methode, um die "Gesamtheit der absoluten Wahrheiten"
zu finden. Sie handelt von idealisierten Gedankenkonstrukten und ist
abhängig von den Spielregeln, die wir dem formalen Denken auferlegen.
Über die Wege der Idealisierung und Modellierung kann sie genutzt werden,
um unsere Welt besser zu verstehen und besser in den Griff zu bekommen.
(Sie kann natürlich auch für Zwecke eingesetzt werden, mit denen man nicht
einverstanden ist – noch ein Grund, sie nicht gering zu schätzen!)
Sie als Disziplin zu verstehen, die nicht nur nützlich ist, sondern
– lässt man sich einmal auf sie ein –
auch faszinierende geistige Abenteuer bereithält, ist vielleicht nicht einmal die
schlechteste Charakterisierung.
|
| | |
| |
| | |
| | | |
Zum Seitenanfang | |
| | |
Von Euklid von Alexandria, dem wir gegen Ende des vorigen Abschnitts bereits begegnet sind,
wird erzählt, er hätte dem Pharao Ptolemaios – ein bisschen frech – gesagt,
es gäbe "keinen Königsweg zur Geometrie". Auch der König muss, wenn er
Geometrie – und Mathematik ganz allgemein – verstehen will, sich mit dieser speziellen
Art den Denkens vertraut machen, sie selbst vollziehen, Erfahrungen machen, aus seinen Fehlern
lernen und sich weiterentwickeln. Auf die Gefahr hin, jetzt in den Tonfall einer Predigt
zu verfallen, wollen wir Ihnen in diesem Sinn einige Tipps auf dem Weg in die Mathematik mitgeben:
- Lassen Sie sich drauf ein!
Viele Menschen haben eine tiefsitzende Scheu vor der Mathematik. Manche haben sogar richtiggehende
Angst davor, andere schlicht eine starke Abneigung. Etliche sagen, sie seien "unbegabt" und
"total ungeeignet" für dieses Fach.
In vielen Fällen stecken Probleme mit Mathematik-Lehrkräften oder
die Angst vor Prüfungssituationen, Versagen und Bloßstellung dahinter.
Versuchen Sie, so gut es geht,
ein bisschen zwischen der Mathematik und der Art, wie Sie sie vermittelt bekommen, zu unterscheiden!
Lasten Sie Motivationsprobleme nicht "der Mathematik" an!
Versuchen Sie, die mathematischen Strukturen, Begriffe, Aufgaben und Methoden
als Bestandteile einer Denktechnologie zu akzeptieren, die im Prinzip jeder Mensch erlernen kann!
- Verstehen ist (fast) alles!
Die Haltung "Ich will's nicht verstehen – ich möchte nur wissen, wie's geht!" bringt
Ihnen nur kurzfristig eine Arbeitseinsparung. A la longue führt sie dazu, dass
Sie sich viel mehr merken müssen als mit ein bisschen Hintergundwissen,
und dass sie Gefahr laufen, den Anschluss verlieren. Der Einstieg in jedes neue Kapitel wird
Ihnen schwer fallen, und Sie werden ständig um eine minimale Orientierung
kämpfen, um Ihre Prüfungen zu bestehen. Das alles ersparen Sie sich, wenn es Ihnen
– sei es alleine oder im Verein mit anderen – gelingt, zu verstehen, was in diesem
Gebiet "abgeht". Lediglich zu "üben", ohne Verständnis Aufgaben zu lösen, ist nicht
nur mühsam, sondern kann zur Einübung und Automatisierung von Fehlern
und fehlerhaften Vorgangsweisen führen. Wussten Sie, dass es in Matura-Arbeiten (Abitur-Arbeiten)
nur so wimmelt vor Fehlern, die auf unverstandenen Stoff der Unterstufe (Sek 1)
zurückgehen?
(Wenn Sie das näher interessiert, sehen Sie sich Mario Wunderls
Dipolmarbeit
SchülerInnenfehler in Mathematikaufgaben der schriftlichen
AHS-Matura
an!)
- Auch das Papier ist eine nützliche Erfindung!
Gerade wenn Sie mit Hilfe von Ressourcen wie mathe online lernen, die am WWW zur Verfügung stehen
und mit dem Computer abgerufen werden, sollten Sie nicht zögern, ein Blatt Papier zur Hand zu
nehmen, um Rechnungen und Notizen aufzuschreiben! "Mathematik lernen am Computer" soll keine
Anleitung sein, alles im Kopf zu lösen.
- Eigene Aufzeichnungen sind Goldes wert!
Ihr Lernprozess im Fach Mathematik wird wahrscheinlich ein längerer sein, der
sich über Jahre erstreckt. Schreiben Sie Dinge, die Ihnen wichtig und nützlich
erscheinen, auf, damit Sie sie später benützen können, und damit Sie sich
später besser an sie erinnern können!
So hat sich beispielsweise eine selbstgeschriebene Formelsammlung schon oft mittel- und langfristig
bezahlt gemacht.
Wir hoffen, diese Seite hat Sie ein wenig neugierig auf mehr Mathematik
gemacht und Sie über Ihre Chancen, das Lernen von Mathematik zu bewältigen,
zuversichtlich gestimmt.
Wir wünschen Ihnen alles Gute!
|
| | |
| |