| | |
| | | |
| |
| | |
| | | |
| |
| | |
Die Differentialrechnung (oder Differenzialrechnung) zählt zu den großen Errungenschaften
der neuzeitlichen Mathematik.
Gemeinsam mit der Integralrechnung ist sie ein Teilgebiet der Analysis.
Um sie verstehen zu können, benötigen wir einige Kenntnisse
aus früheren Kapiteln, die wir kurz zusammenfassen:
Eine (reelle) Funktion f kann
- als Zuordnung betrachtet werden (jeder reellen Zahl x
aus dem Definitionsbereich von f wird eine
reelle Zahl f(x)
zugeordnet) oder
- als Ausdruck der Abhängigkeit einer Größe von einer
anderen (die Größe f
hängt vom Wert der Größe x
ab und wird daher als f(x) geschrieben).
Eine Funktion kann zeichnerisch dargestellt werden, indem in einem Diagramm die
möglichen x-Werte auf der horizontalen Achse und zu
jedem x-Wert der
zugehörige Funktionswert f(x) auf der vertikalen Achse aufgetragen wird.
Die Menge aller so entstehenden Punkte in der Zeichenebene ist der Graph der Funktion
- im Allgemeinen ist er eine Kurve, die die Eigenschaften der Funktion
widerspiegelt. Wird die vertikale Koordinate mit dem Symbol y
bezeichnet, so ist der Graph die Menge aller Punkte
(x, y),
für die y = f(x)
gilt.
| | | |
Integralrechnung
Funktionen 1
| |
| | |
Beispiel: Die durch f(x) = x2
definierte Funktion
(manchmal auch in der Form
f : x ® x2
angeschrieben)
ordnet jeder Zahl ihr Quadrat zu. Ihr Graph ist eine nach oben offene Parabel, deren
Scheitel im Ursprung liegt.
Der Anstieg (die Steigung) einer Geraden in einem
xy-Koordinatensystem
ist der Quotient der Kathetenlängen eines Steigungsdreiecks
(Dy/Dx).
Wir können diese Größe von Verkehrsschildern ablesen: Der Anstieg einer mit
dem Hinweis "15%" gekennzeichneten Straße ist 0.15
(wobei die y-Achse als vertikal zu denken ist).
Ist eine Gerade durch die Gleichung
y = kx + d
gegeben, d.h. ist sie der Graph der linearen Funktion
f(x) = kx + d,
so ist ihr Anstieg der Wert der Kontante k.
| | | |
Quadratische Funktionen
Anstieg einer Geraden
| |
| | |
Schließlich wäre es günstig, wenn Sie bereits von Grenzprozessen und
dem Begriff des Grenzwerts gehört haben.
Wir werden allerdings in diesem Kapitel nur wenig (und eher intuitiven) Gebrauch von ihnen
machen.
|
| | |
Grenzprozesse
| |
| | |
| | | |
Zum Seitenanfang | |
| | |
Wir wissen, was der Anstieg einer Geraden ist - macht es auch Sinn, vom
Anstieg einer Kurve zu sprechen? Wir wollen zunächst nicht allzu streng sein und
uns von der Intuition leiten lassen: Eine Kurve kann ihre "Richtung" ändern, sie kann in verschiedenen
Punkten unterschiedlich "steil" sein. Macht es also Sinn, von der Richtung und vom Anstieg einer
Kurve in einem Punkt zu sprechen? Ja, das macht Sinn, vorausgesetzt, die Kurve besitzt
in dem betreffenden Punkt eine Tangente (d.h. sie macht dort keinen Knick). Dann bezeichnen wir
als Richtung der Kurve die Richtung der Tangente und als
Anstieg der Kurve den Anstieg der Tangente.
Das wollen wir auf den Graphen einer Funktion anwenden. Wir vereinbaren:
| | | |
Tangente
(in Vorbereitung)
| |
| | |
|
Sei f eine (reelle) Funktion. Die Ableitung von
f an der Stelle x
ist der Anstieg der Tangente an den Graphen von f
im Punkt (x, f(x)).
Sie wird mit dem Symbol f '(x)
bezeichnet (ausgesprochen als "f-Strich von x"
oder "f-Strich an der Stelle x").
|
Bemerkung: Dabei ist natürlich vorausgesetzt, dass der Graph von f
im Punkt (x, f(x)) überhaupt eine Tangente besitzt.
Diese Vereinbarung ist daher vorerst nicht als präzise Definition
des Begriffs der Ableitung aufzufassen, sondern eher als
Grundidee, von der wir ausgehen.
Damit 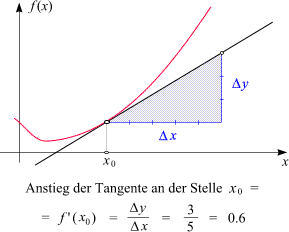 wissen wir im Prinzip, was die
Ableitung ist. Stellen wir uns vor, eine Funktion f
sei gegeben, ihr Graph sei gezeichnet, und wir sollten die Ableitung an einer
gegebenen Stelle x0 bestimmen.
Wir haben noch kein Verfahren zur Hand, dieses so genannte Tangentenproblem
mittels einer Rechnung zu lösen, aber um die gewünschte
Ableitung näherungsweise aus dem Diagramm, das den Graphen zeigt, abzulesen, legen wir
- so genau es geht - die Tangente
durch den Punkt
(x0, f(x0))
und vermessen ihren Anstieg mit Hilfe eines Steigungsdreiecks. Das ist im Bild rechts anhand eines
Beispiels dargestellt. Auf die Größe des Steigungsdreiecks kommt es dabei nicht
an. Im gezeigten Beispiel ist es so gewählt, dass
Dx = 5 ist,
und danach wird Dy als
3 abgelesen. Die Ableitung ist dann der Quotient
Dy/Dx,
also 3/5 oder 0.6.
Eine andere Möglichkeit wäre, ein Steigungsdreieck zu zeichnen, für das
Dx = 1 ist,
womit der Anstieg direkt als
Dy abgelesen wird.
Klicken Sie hier, um die Anzeige dieses normierten Steigungsdreiecks
an- und abzuschalten.
Das nebenstehende Applet erlaubt es Ihnen, diesen Zusammenhang zwischen Ableitung und Tangentenanstieg
in einer interaktiven Weise durchzuspielen und den Umgang mit den neuen Begriffen
zu üben.
| | | |
Applet
Zur Definition
der Ableitung
| |
| | |
Diese Idee der Ableitung hat weitreichende Konsequenzen und führt in zwangloser Weise zu weiteren Begriffen, die dazu
dienen, Funktionen zu charakterisieren. Insbesondere ist die Ableitung einer Funktion f
selbst wieder eine Funktion: Sie ordnet jedem
x die Ableitung von f
an der Stelle x zu und wird mit dem Symbol
f ' bezeichnet.
Um diesen Aspekt zu betonen, kann man f '
auch Ableitungsfunktion nennen. Ihr Funktionswert an der Stelle
x ist f '(x),
in Übereinstimmung mit der oben eingeführten Schreibweise. Als Funktion besitzt
f ' natürlich auch einen Graphen.
Zwischen den Eigenschaften einer Funktion und den Eigenschaften ihrer Ableitung bestehen wichtige Zusammenhänge.
Eine schöne Illustration dafür ergibt sich aus dem Bild einer Straße,
die auf und ab durch eine Landschaft führt.
(Die y-Achse ist dabei als vertikal zu denken).
Rufen Sie mit dem nebenstehenden Button eine solche Illustration auf. Sie werden dabei auf
Begriffe wie Hochpunkt, Tiefpunkt, Maximum, Minimum, Extremum und Wendepunkt
und auf einen Zusammenhang mit dem Monotonieverhalten einer Funktion
stoßen, die uns alle im Laufe dieses Kapitels noch begegnen werden.
| | | |
Steigungen in der
| |
| | |
Eine besonders nützliche Illustration der Ableitung kommt aus der Physik:
Ist s(t) der Ort, an dem ein Körper zur Zeit
t ist, so kann dessen Bewegung durch den Graphen der
Funktion
s ® s(t)
(die so genannte Weltlinie) zeichnerisch dargestellt werden.
Handelt es sich dabei um eine gleichförmige Bewegung, so ist die Weltlinie eine Gerade, und ihr
Anstieg ist die Geschwindigkeit (Ds/Dt, d.h.
zurückgelegter Weg durch benötigte Zeit).
Ist die Bewegung beschleunigt, so ist die Weltlinie eine Kurve. Den Anstieg der Tangente an die
Weltlinie im Punkt
(t0, s(t0)),
d.h. die Ableitung s '(t0), bezeichnen wir als
Momentangeschwindigkeit des Körpers zu Zeit
t0.
Da die Ableitung einer Funktion wieder eine Funktion ist, können wir
höhere Ableitungen betrachten: Die Ableitung der Ableitung von f heißt zweite Ableitung
und wird mit dem Symbol f '' bezeichnet.
f ''(x) ist der Anstieg der Tangente
an den Graphen von f ' im
Punkt (x, f '(x)).
In analoger Weise kann die dritte Ableitung f '''
betrachtet werden, usw.
Die n-te Ableitung wird auch als
f (n) geschrieben.
| | | |
| |
| | |
Es wird Ihnen später sehr helfen, wenn Sie in der Lage sind, Graphen von Funktionen und
Ableitungen zu verstehen und aufeinander zu beziehen.
Mit Hilfe der drei nebenstehenden Applets können Sie das ein bisschen üben, indem
Sie die Ableitungen von Funktionen erkennen.
Von allen beteiligten Funktionen sind nur die Graphen gegeben -
mehr müssen Sie über sie nicht wissen.
Der Schwierigkeitsgrad ist ansteigend, aber in allen Fällen kommen Sie mit
dem bisher Gesagten (und vielleicht einer kleinen Portion detektivischen Herangehens) aus.
Damit kommen wir zum Ende unseres "intuitiven" Abschnitts.
Eine Funktion abzuleiten oder zu differenzieren heißt, ihre Ableitung zu bestimmen.
Wir haben vorerst die Grundidee für diesen Prozess formuliert.
Was uns aber noch fehlt, ist ein Verfahren, Ableitungen konkret auszurechnen
(und ein Kriterium, wann sie überhaupt existieren).
Damit - und mit einigen Konsequenzen - werden wir uns
im Rest dieses Kapitels beschäftigen.
|
| | |
Applets
Ableitungs-Puzzles
1 2 3
| |
| | |
| | | |
Zum Seitenanfang | |
| | |
Wie wollen nun berechnen, was wir im vorigen Abschnitt als Idee formuliert haben: den Anstieg der
Tangente an einen Funktionsgraphen. Dazu nehmen wir zunächst ganz allgemein an, eine
reelle Funktion f und eine Stelle x0
seien gegeben, und die Aufgabe besteht darin, den Anstieg der Tangente an den Graphen im Punkt
(x0, f(x0))
zu ermitteln. Wir gehen in zwei Schritten vor.
1. Schritt: Wir berechnen zunächst den Anstieg einer Sekante,
d.h. einer Geraden, die den Graphen von f in zwei
Punkten schneidet, und zwar einerseits im gegebenen Punkt
(x0, f(x0)),
andererseits in einem Nachbarpunkt
(x0 + e, f(x0 + e)),
wobei der Wert von e zunächst nicht näher angegeben wird.
Mit anderen Worten, wir gehen von x0 ein
Stück e nach rechts oder links (je nach dem Vorzeichen von e)
und berechnen den Anstieg der Geraden durch die beiden Punkte des Graphen, die wir
in der folgenden Zeichung als P und Q bezeichnen:
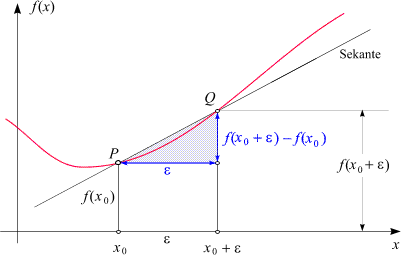
Die Katheten des eingezeichneten Steigungsdreiecks sind
Dx = e
und
Dy = f(x0
+ e) - f(x0),
womit der Anstieg der Sekante, d.h. der Quotient Dy/Dx,
als
geschrieben werden kann. Da Zähler und Nenner nichts anderes sind als die Differenzen der Koordinaten der Punkte
P und Q,
wird diese Größe Differenzenquotient genannt.
2. Schritt: Wir haben zwar jetzt den Anstieg der Sekante
durch die Punkte P und Q
berechnet, worauf wir aber letztlich hinaus wollen, ist der Anstieg der Tangente im Punkt P.
Wenn wir nun e (genauer: seinen Betrag) immer kleiner machen, sollte sich die Sekante der
Tangente annähern. Allerdings können wir nicht einfach
e = 0 in (1)
einsetzen, denn dann erhalten wir den sinnlosen Ausdruck 0/0.
Das ist klar, denn dann fallen die Punkte
P und Q
ja zusammen und können daher keine Gerade bestimmen. Was wir aber tun können, ist, von einer echten Sekante auszugehen (d.h. von einem
Wert e ¹ 0) und
e schrittweise immer näher an
0 heranführen. Wir können also beispielsweise nacheinander
e = 1,
e = 1/2,
e = 1/3,...
setzen. Für jeden dieser Werte von e bekommen wir
einen Differenzenquotienten vom Typ (1), und die so entstehende Folge von Differenzenquotienten
sollte sich dem gesuchten Tangentenanstieg annähern.
Klicken Sie hier, um eine kleine Animation, die diesen
Vorgang illustriert, an- und und abzuschalten.
Was wir also im Sinn haben, ist, die Ableitung
als Grenzwert des Differenzenquotienten (1) für gegen 0 strebendes e zu definieren.
Symbolisch schreiben wir ihn als
| | | |
Folgen und
Grenzwerte
und
Grenzwerte reeller Funktionen
| |
| | |
| |
|
|
f(x0
+ e) - f(x0)
e |
. |
| f '(x0) = |
lim |
| |
e ® 0 |
|
(2) |
Den ersten Teil dieses Ausdrucks sprechen wir als "Limes Epsilon gegen 0"
aus.
Die nebenstehende Flash-Animation illustriert noch einmal diesen Grenzübergang.
Lassen Sie sich nicht davon stören, dass in ihr statt des Symbols
e der Buchstabe h
verwendet wird.
| | | |
Flash
Die Ableitung als
Grenzwert
| |
| | |
Beispiel: Wir betrachten die Funktion f(x) = x2
und berechnen die Ableitung an der Stelle x0 = 3.
Der Differenzenquotient (1) berechnet sich zu
(3
+ e)2 -
32
e |
= |
9
+ 6 e +
e2 -
9
e |
= |
6 e + e2
e |
=
6 + e . |
|
(3) |
Vollziehen Sie die Vereinfachungsschritte nach! Beachten Sie, dass man in den ersten drei Ausdrücken
nicht einfach e = 0
setzen kann, da sich dann 0/0 ergäbe.
Mit dem letzten Ausdruck können wir den Grenzübergang
e ® 0
aber ganz leicht durchführen:
Wenn e gegen 0
strebt, rückt
6 + e
immer näher an die Zahl 6 heran, d.h. erst jetzt
ist es zulässig, e = 0 zu setzen.
Unser Resultat ist also: f '(3) = 6.
In Worten: Der Anstieg der Tangente an den Graphen der Funktion
x ® x2
im Punkt
(3, 9) ist 6.
Damit sind wir prinzipiell in der Lage, die Ableitung zahlreicher Funktionen zu berechnen.
Nicht immer ist die Berechnung so einfach wie im Beispiel (3), aber wir werden unten
einige Hilfsmittel kennen lernen, die das Differenzieren wesentlich erleichtern.
Wir beschließen diesen Abschnitt mit ein paar grundsätzlichen Bemerkungen über den
Grenzübergang e ® 0,
der in Formel (2) durchzuführen ist.
Wenn Sie daran nicht interessiert sind, so überspringen Sie sie einfach
oder kehren später zu ihnen zurück.
Bemerkungen zur Definition der Ableitung:
Der wichtigste Punkt an Formel (2) ist der
Grenzübergang e ® 0.
Wir haben ihn bisher so charakterisiert, dass
"e schrittweise gegen 0
strebt". Allerdings gibt es viele Arten, e schrittweise
gegen 0 streben zu lassen:
Anstatt nacheinander
e = 1,
e = 1/2,
e = 1/3,...
zu setzen, könnten wir genausogut
e = -1,
e = -1/2,
e = -1/3,...
oder
e = 1,
e = -1/2,
e = 1/4,
e = -1/8,...
setzen. Da e nichts anderes als die Differenz der
x-Koordinaten von
P und Q
ist, entsprechen diese Möglichkeiten den verschiedenen Arten, wie der Punkt Q
der obigen Zeichnung an den Punkt P
herangeführt werden kann:
Ist |e| klein, so liegt Q
nahe bei P. Ist
e > 0, so liegt
Q rechts von P. Ist
e < 0, so liegt
Q links von P.
Für jede der vielen Möglichkeiten, e schrittweise gegen 0 streben zu lassen,
erhalten wir eine Folge von Differenzenquotienten.
Falls sich in all diesen Fällen immer derselbe Grenzwert ergibt, so bezeichnen
wir ihn als die Ableitung f '(x0),
und wir nennen die Funktion f "an der Stelle
x0 differenzierbar".
Durch diese Präzisierung bekommt übrigens auch der Begriff der Tangente
an einen Funktionsgraphen (soweit sie nicht parallel zur vertikalen Achse ist) eine genaue Bedeutung:
Sie ist die Gerade mit Anstieg f '(x0)
durch den Punkt (x0, f(x0)).
Der nebenstehende Button ruft einige weitere grundsätzliche Bemerkungen zu
diesem Thema auf. Ein Beispiel für eine Funktion, die an einer Stelle nicht differenzierbar ist
(die Betragsfunktion), können Sie mittels des zweiten nebenstehenden Buttons aufrufen.
Ist eine Funktion f an allen Stellen eines (offenen) Intervalls differenzierbar,
so ist sie in diesem Intervall stetig. Ist auch ihre Ableitung eine stetige Funktion, dann
nennt man sie "stetig differenzierbar". Das ist für die meisten Funktionen,
die beim Mathematiklernen auftreten, der Fall.
Es lassen sich aber Beispiele konstruieren, in denen die Ableitung einer differenzierbaren
Funktion unstetig ist. Weitere Überlegungen
zur Differenzierbarkeit einer Funktion und zum Zusammenhang zur Stetigkeit
wollen wir uns für das zweite Differenzieren-Kapitel aufheben.
|
| | |
Grundsätzliche
für eine nicht-
differenzierbare Funktion
Differenzieren 2
| |
| | |
| Beispiele und Schreibweisen |
| | | |
Zum Seitenanfang | |
| | |
Formel (2) versetzt uns in die Lage, Ableitungen zu berechnen.
Sie ist in gewisser Weise der Ausgangspunkt der Differentialrechnung.
Bei ihrer Herleitung - und auch im Beispiel
(3) - haben wir uns auf die Ableitung an einer
fixen gegebenen Stelle x0
beschränkt. Um den Charakter der Ableitung als Funktion zu unterstreichen,
können wir die betreffende Stelle einfach als
x bezeichnen
und (2) in der Form
| |
|
|
f(x
+ e) - f(x)
e |
. |
| f '(x) = |
lim |
| |
e ® 0 |
|
(4) |
schreiben. Die Berechnung von Ableitungen kann in einem Zug für alle x
ausgeführt werden. Sehen wir uns vier Beispiele an:
Beispiel 1: Wir betrachten wieder die Funktion f(x) = x2,
berechnen aber nun die Ableitung an einer beliebigen Stelle x.
Die nötige Umformung verläuft ganz ähnlich wie (3). Der Differenzenquotient ist
(x
+ e)2 -
x2
e |
= |
x2
+ 2xe +
e2 -
x2
e |
= |
2xe + e2
e |
=
2x + e. |
|
(5) |
Nun können wir den Grenzübergang
e ® 0
durchführen und erhalten
In anderen Worten: Die Ableitung der Funktion x ® x2
ist die Funktion x ® 2x.
Das ist ein schönes Resultat. Wer hätte gedacht, dass die Anstiege der Tangenten an eine Parabel durch eine derart einfache Formel gegeben sind?
Setzen wir x = 3, so ergibt sich
das bereits oben erzielte Resultat f '(3) = 6.
Weiter ist f '(0) = 0, was einfach besagt, dass
die Tangente an den Graphen an der Stelle x = 0 den Anstieg 0 hat,
d.h. parallel zur x-Achse ist.
In den Bereichen x > 0 (x < 0)
ist der Anstieg positiv (negativ). Die Tangente ist umso steiler, je größer
der Betrag von x ist.
Sehen Sie sich den Graphen von f an (z.B. mit dem Funktions-Plotter) und
überzeugen Sie sich von diesen Eigenschaften!
Beispiel 2: Mit der Funktion f(x) = x3
können wir auf die gleiche Weise verfahren. Rechnen Sie selbst nach, dass
(x
+ e)3 -
x3
e |
=
3x2 +
3ex
+ e2 . |
|
(7) |
gilt. Der Grenzwert dieses Ausdrucks für e ® 0
ist 3x2, womit sich
f '(x) = 3x2
ergibt.
In anderen Worten: Die Ableitung der Funktion x ® x3
ist die Funktion x ® 3x2.
Die Ableitung wird nie negativ. Wegen f '(0) = 0
ist die Tangente an den Graphen an der Stelle x = 0
parallel zur x-Achse.
Sehen Sie sich den Graphen von f an (z.B. mit dem Funktions-Plotter), um
sich von diesen Eigenschaften zu überzeugen!
Beispiel 3: Nun betrachten wir ein Beispiel, das so einfach ist, dass es eigentlich nichts
zu rechnen gibt: die konstante Funktion
f(x) = c,
wobei c eine vorgegebene und festgehaltene
Zahl ist. In diesem Fall verschwindet der Differenzenquotient, denn
für alle x und
e gilt
f(x
+ e) - f(x) = c - c = 0.
Da er nicht von e abhängt, entfällt das Bilden des Grenzwerts
e ® 0,
und wir erhalten
f '(x) = 0
(für alle x).
In anderen Worten: Die Ableitung der konstanten Funktion
x ® c
ist die Funktion
x ® 0.
("Die Ableitung einer konstanten Funktion ist Null").
Wir können dieses Resultat auch geometrisch verstehen, denn der Graph der konstanten Funktion
ist eine Gerade parallel zur x-Achse (d.h. mit Anstieg 0).
In diesem Fall stimmen Graph, Sekante und Tangente miteinander überein.
| | | |
Grenzwerte reeller Funktionen
| |
| | |
Beispiel 4: Als letztes Beispiel betrachten wir eine allgemeine lineare Funktion
(Funktion erster Ordnung), definiert durch einen Term der Form
f(x) = kx + d,
wobei k und d
vorgegebene und festgehaltene Zahlen sind. Der Differenzenquotient ist in diesem Fall durch
k gegeben (rechnen Sie nach!), hängt also (wie im vorigen Beispiel) nicht von
e ab, womit wir
f '(x) = k
erhalten.
In anderen Worten: Die Ableitung der linearen Funktion
x ® kx + d
ist die konstante Funktion
x ® k.
Auch dieses Resultat können wir geometrisch verstehen: Der Graph unserer linearen
Funktion ist eine Gerade mit Anstieg k, weshalb
Graph, Sekante und Tangente miteinander übereinstimmen.
Das Resultat des vorigen Beispiels erhalten wir als Spezialfall, indem wir
k = 0 und
d = c
setzen.
Rede- und Schreibweisen
- Zur Kennzeichnung der Ableitung einer termdefinierten Funktion kann der Funktionsterm
mit einem Strich versehen werden.
So können wir beispielsweise die Aussage, dass
die Ableitung der Funktion x ® x2
die Funktion x ® 2x ist,
in der Form
schreiben.
- Da nicht jede Variable mit dem Symbol x
bezeichnet wird, kennzeichnet man diese beim Bilden der Ableitung mit dem Wort "nach".
Man sagt einfach: f '(x) ist die
Ableitung von f(x) nach x.
Eine Funktion nach r abzuleiten
(oder nach r zu differenzieren) heißt,
die Ableitung einer Funktion nach r zu bilden.
Außerdem muss nicht immer dazugesagt werden, dass es sich bei einem Ausdruck (Term) um eine Funktionsdarstellung handelt.
So kann man beispielsweise einfach sagen: Die Ableitung von u3
nach u ist gleich
3u2.
- Der auf die Stellen x
und x + e
bezogene Differenzenquotient (Anstieg der Sekante) wird manchmal in der Form
Dy/Dx
oder
Df/Dx
angeschrieben, wobei
Dx = e
und
Dy º Df = f(x
+ e) - f(x)
ist.
Im Grenzübergang Sekante ® Tangente streben Dx und Df beide gegen 0, wodurch der Quotient Df/Dx
nach diesem Übergang zum sinnlosen Ausdruck 0/0 wird.
In der historischen Entwicklung der Differentialrechnung hat man sich zunächst vorgestellt, Dx und Df werden zwar "unendlich klein", aber auf eine Weise, die es nach wie vor erlaubt,
ihren Quotienten zu bilden.
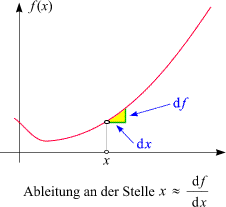Diese "unendlich kleinen" Größen wurden als
dx und df (bzw. dy)
bezeichnet (man nannte sie "infinitesimal" oder "Differentiale"), und die Ableitung
kurzerhand als Quotient df/dx
bzw. dy/dx
angeschrieben. Intuitiv kann man sich unter den Differentialen die Kathetenlängen eines Steigungsdreiecks
vorstellen, das so klein ist, dass der Unterschied zwischen Sekante und Tangente nicht ins
Gewicht fällt: siehe die Skizze rechts.
df ist die Änderung des Funktionswerts,
wenn sich das Argument, d.h. der Wert der unabhängigen Variablen, von der Stelle x ausgehend um dx ändert.
Je kleiner das Steigungsdreieck ist, umso weniger
unterscheidet sich der Quotient df/dx
von der Ableitung - um aber einen exakten Ausdruck für letztere
zu bekommen, hat man sich vorgestellt, dass es sich um ein "unendlich kleines" Steigungsdreieck handelt.
Heute sind wir - dank des modernen Grenzwertbegriffs
- in der Lage, diese Dinge mathematisch genauer zu formulieren, aber
bis heute wird die Ableitung als Differentialquotient bezeichnet, und auch die
Schreibweise hat in gewissem Sinn überlebt.
Dazu betrachten wir als Beispiel wieder die Funktion f(x) = x2
und bezeichnen die Koordinaten in der Ebene, in der ihr Graph lebt, mit
x und y.
Dann sind - neben (6) und (8) -
folgende (auf Gottfried Wilhelm von Leibniz zurückgehende) Schreibweisen für die Ableitung gebräuchlich:
dy
dx |
= |
df
dx |
= |
df(x)
dx |
= |
d(x2)
dx |
= |
d
dx |
f(x) |
= |
d
dx |
x2 |
=
2x . |
|
(9) |
Die erste Variante wird ausgesprochen als "d-y-nach-d-x".
In den letzten beiden Varianten bedeutet der formale Quotient d/dx
(ausgesprochen: "d-nach-d-x") die Aufforderung, den rechts von ihm stehenden Funktionsausdruck
nach x abzuleiten.
Analog dazu steht beispielsweise d/du
für das Bilden der Ableitung nach u.
Das ist etwa sinnvoll für die Ableitung einer Funktion, deren Termdarstellung
mehrere Symbole enthält, z.B. wenn
a für eine festgehaltene Zahl (Konstante) steht:
d(a3u2)/du = 2a3u
(was aus den unten zu besprechenden Ableitungsregeln folgt).
- Für höhere Ableitungen wird auch die Schreibweise
d2y/dx2
(ausgesprochen: "d-zwei-y-nach-d-x-Quadrat") oder
d2f(x)/dx2,
bzw. als Aufforderung, die zweite Ableitung zu bilden,
d2/dx2
(ausgesprochen: "d-zwei-nach-d-x-Quadrat")
verwendet. Manchmal findet man für letzteres die symbolische Schreibweise
(d/dx)2
als Aufforderung, zweimal zu differenzieren.
- Um die Ableitung an einer bestimmten Stelle, z.B. 0,
zu bezeichnen, ist die Schreibweise f '(0)
am günstigsten. Es kann aber auch (x2) ' |x=0
oder eine ähnliche Form verwendet werden.
(Der senkrechte Strich | hat die Bedeutung "an der Stelle" und wird auch so ausgesprochen).
- Manchmal wird anstelle eines Strichs ein Punkt über das Funktionssymbol
gesetzt (z.B. in der Physik, wenn die Variable die Zeit ist). Statt
s'(t) wird dann
 |
| s(t) |
(ausgesprochen: "s-Punkt von t") geschrieben.
Die zweite Ableitung wird dann durch zwei Punkte
(ausgesprochen "s-zwei-Punkt") gekennzeichnet.
Neues Vokabular zu lernen, ist nicht immer leicht. All diese Bezeichnungen und Symbole haben ihre Vor- und Nachteile.
Wer viel mit Ableitungen zu tun hat, wird nach einiger Zeit dankbar sein, mehrere Möglichkeiten
zur Schreib- und Ausdrucksweise zur Verfügung zu haben.
Lassen Sie sie zunächst ein bisschen auf sich wirken und
kommen Sie bei Bedarf später wieder auf diese Seite zurück!
|
| | |
Funktionen erster
Ordnung
| |
| | |
| | | |
Zum Seitenanfang | |
| | |
Aufgrund der überragenden Bedeutung des Begriffs der Ableitung in der modernen Mathematik, aber auch
in anderen Gebieten wie in der Physik, wünscht man sich Regeln, die es erlauben,
Funktionen schnell und ohne große Anstrengung zu differenzieren. Glücklicherweise
existieren solche Regeln. Mit ihrer Hilfe, kann man die Zahl der Fälle, in denen die Formel
(4) angewandt werden muss, auf ein Minimum reduzieren.
Stellen wir uns vor, zwei (reelle) Funktionen f und g
seien gegeben, und ihre Ableitungen
f ' und
g' seien bekannt.
Aus f und g
können wir weitere Funktionen konstruieren, insbesondere
x ® c f(x),
wobei c eine vorgegebene Zahl (d.h. eine Konstante) ist,
die Summe x ® f(x) + g(x),
das Produkt x ® f(x)g(x),
den Quotienten x ® f(x)/g(x),
die Verkettung
x ® f(g(x))
und schließlich die zu f inverse Funktion (Umkehrfunktion), die wir in der Form
f ® x( f ) anschreiben.
| | | |
Funktionen kombinieren
inverse Funktion
| |
| | |
Die Ableitungen all dieser Funktionen können wir auf jene von
f und g
zurückführen, was das Differenzieren zu einer relativ einfachen Angelegenheit macht
(die, wie wir unten sehen werden, auch von Computerprogrammen durchgeführt werden kann):
1.) Multiplikation mit einer Konstanten:
| | | |
| |
| | |
In Worten: die Ableitung eines Vielfachen ist das Vielfache der Ableitung.
Beispiel: (4x2) ' = 8x,
wobei wir verwendet haben, dass uns die Ableitung
(x2) ' = 2x
bereits bekannt ist, vgl. (8).
2.) Summe zweier Funktionen:
| | | |
| |
| | |
|
( f(x) + g(x)) '
= f '(x) + g'(x) |
|
(11) |
In Worten: die Ableitung einer Summe ist die Summe der Ableitungen.
Beispiel 1: (x2 + x) ' = 2x + 1,
wobei wir verwendet haben, dass uns die Ableitungen
(x2) ' = 2x
und x' = 1
bereits bekannt sind.
Beispiel 2: (x2 - 5x + 7) ' = 2x - 5,
wobei wir verwendet haben, dass uns die Ableitungen
(x2) ' = 2x
und (-5x + 7) ' = -5
bereits bekannt sind. (Für letzteres siehe die Beispiele 3 und 4 oben).
In der Praxis ist es oft nützlich, die Regeln (10) und (11) zu kombinieren, d.h. in
einer Rechnung mehrfach anzuwenden.
In der Sprache der höheren Mathematik drücken sie die Tatsache aus, dass das
Bilden der Ableitung eine "lineare Operation" ist.
Beispiel 1: (3x2 - 2x + 9) ' = 6x - 2,
wobei wir lediglich die Ableitungen
(x2) ' = 2x,
x' = 1
und
1' = 0 kennen müssen.
Beispiel 2: Unter der Verwendung von (10) mit
c = -1 und (11)
folgt: Die Ableitung einer Differenz ist die Differenz der Ableitungen:
( f(x) - g(x)) '
= f '(x) - g'(x).
3.) Produktregel:
| | | |
| |
| | |
|
( f(x) g(x)) '
= f '(x) g(x) + f(x) g'(x) |
|
(12) |
Sehen Sie sich die Struktur der rechten Seite dieser Formel genauer an, denn Sie werden sie vielleicht selbst oft
anwenden. Im ersten Summanden wird nur
f differenziert, im zweiten nur
g.
Beispiel: Wir berechnen die Ableitung der Funktion
x ® (2x + 3) (x2 + 4).
Wir könnten den Funktionsterm erst ausmultiplizieren, jeden Summanden getrennt differenzieren und dann Regel (11)
anwenden. (Machen Sie das als Übungsaufgabe!). Wir können aber die gegebene Funktion auch als Produkt der
Funktionen
f(x) = 2x + 3
und
g(x) = x2 + 4
auffassen und die Produktregel (12) anwenden:
Mit
f '(x) = 2
und
g'(x) = 2x
erhalten wir als Ableitung
((2x + 3) (x2 + 4)) ' = 2(x2 + 4) + (2x + 3) 2x,
was durch Ausmultiplizieren weiter vereinfacht werden kann.
Die grün dargestellten Terme sind die Faktoren
der gegebenen Funktion, die blau dargestellten sind deren Ableitungen.
Berechnungen dieser Art zu beherrschen ist mit ein bisschen Übung nicht schwierig, und es
macht sich bezahlt!
4.) Quotientenregel:
| | | |
| |
| | |
| ( |
f(x)
g(x) |
) |
' |
= |
f '(x) g(x)
- f(x) g'(x)
g(x)2 |
|
(13) |
Sie ist etwas komplizierter als die Produktregel, aber ebenfalls äußerst nützlich.
Beispiel 1:
| ( |
3x2 + 7x
2x + 1 |
) |
' |
= |
(6x + 7) (2x + 1)
- (3x2 + 7x) 2
(2x + 1)2 |
, |
|
was ab hier weiter vereinfacht werden kann. (Wieder sind die gegebenen Terme
grün und deren Ableitungen blau dargestellt).
Klarerweise gilt dieses Resultat nur im Definitionsbereich der differenzierten Funktion, d.h. für alle
x ¹ -1/2.
Beispiel 2: Als Spezialfall von (13) für
f(x) = 1
ergibt sich die Regel
(1/g(x)) '
=
- g'(x)/g(x)2
für die Ableitung des Kehrwerts einer Funktion.
Beispiel 3: Als Spezialfall von Beispiel 2 für
g(x) = x
ergibt sich
(1/x) ' = -1/x2.
5.) Kettenregel:
| | | |
| |
| | |
| ( f(g(x)) ) ' =
f '(g(x)) g'(x) |
|
(14) |
Um diese Regel zu verstehen, müssen Sie auf die genaue Schreibweise achten.
Die rechte Seite besteht aus zwei Faktoren:
- Der erste, f '(g(x)),
kommt zustande, indem zuerst die Ableitung der Funktion f
gebildet wird (wenn man will, kann man f in der Form
f : g ® f(g)
schreiben und die Ableitung
f ' : g ® f '(g)
bestimmen) und danach anstelle der Variable
der Ausdruck g(x)
eingesetzt wird. Man kann diesen Faktor auch (etwas salopp) als Ableitung von
f nach g
bezeichnen.
Manchmal wird er auch äußere Ableitung genannt (obwohl dieser Begriff in der
höheren Mathematik noch eine andere Bedeutung hat, die uns hier aber nicht interessiert).
- Der zweite, g'(x),
die Ableitung von g nach x,
wird auch als innere Ableitung bezeichnet.
Die Kettenregel wird auch manchmal in der folgenden (Leibnizschen) Form
| | | |
| |
| | |
angeschrieben, die ihre Struktur noch deutlicher hervorhebt.
Dabei wurde die in (9) vorgestellte Schreibweise verwendet.
Intuitiv kann man sich unter den Größen, die hier vorkommen, kleine ("infinitesimale") Änderungen
vorstellen: Ändert sich x um ein Stück
dx, so ändert sich
g um ein Stück dg,
und daher wiederum ändert sich f um
ein Stück df.
Gleichung (14' ) drückt eine - triviale - Beziehung zwischen diesen drei Größen aus,
die, im Grenzwert beliebig kleiner Änderungen, zu einer Beziehung dreier Ableitungen wird.
Wir können sie so in Worte fassen: Hängt f
nur über g von
x ab, so ist die Ableitung von
f nach x
gleich dem Produkt aus der Ableitung
von f nach g
(wobei g als Variable behandelt wird)
und der Ableitung
von g nach x.
Nachbemerkung: Unter Verwendung der Schreibweise
f o g
für die Verkettung
x ® f(g(x))
kann die Kettenregel (14) auch in der kompakten Form
geschrieben werden.
Beispiel: Wir wollen die Ableitung der Funktion
u(x) = (5x2 + 3x)2
berechnen. Sie kann als Verkettung der Funktionen
f(g) = g2
und
g(x) = 5x2 + 3x
aufgefasst werden. Beide Funktionen können wir leicht ableiten.
Zunächst ist
f '(g) = 2g.
Der erste Faktor auf der rechten Seite von (14) ist daher
f '(g(x)) = 2(5x2 + 3x).
Der ganze Trick besteht darin, g(x),
also den Term 5x2 + 3x,
so zu behandeln, als wäre er eine einzige Variable!
Als zweiter Faktor kommt die innere Ableitung
g'(x) = 10x + 3 hinzu.
Unser Resultat lautet daher
u'(x) = 2(5x2 + 3x) (10x + 3).
6.) Ableitung der inversen Funktion (Umkehrfunktion):
| | | |
| |
| | |
Diese Regel besagt: Die Ableitung einer Funktion
f : x ® f(x)
ist gleich dem Kehrwert der Ableitung der zu f
inversen Funktion
x : f ® x( f ).
Anders ausgedrückt: Die Ableitung von
f nach x
ist gleich dem Kehrwert der Ableitung von
x nach f.
(Genauer: Die linke Seite ist die Ableitung der Funktion f
an einer Stelle x, im Nenner der rechten Seite
steht die Ableitung der zu f inversen Funktion
an der entsprechenden Stelle f = f(x).
Um den Formalismus nicht aufzublasen, haben wir die Funktionen und die Stellen
mit denselben Buchstaben bezeichnet).
Wir können (15) auch in der (Leibnizschen) Form
schreiben, siehe (9) für die Schreibweise.
Beachten Sie, dass das Symbol f bei der inversen Funktion
die unabhängige Variable bezeichnet! Wie (14' )
ist auch diese Rechenregel intuitiv einleuchtend:
Ändert sich x um ein Stück
dx, so ändert sich
f um ein Stück df
(und umgekehrt!).
Die Differenzenquotienten
df /dx
und dx/df
sind daher die Kehrwerte voneinander. Im Grenzwert beliebig kleiner Änderungen
wird daraus die Aussage (15) für die Ableitungen.
Diese Konstruktion funktioniert natürlich nur an jenen Stellen, an denen die
Ableitung von f existiert und ungleich
0 ist.
Wir können sie auch von einem geometrischen Standpunkt aus verstehen:
Der Graph der zu f inversen Funktion
geht aus jenem von f
durch Spiegelung an der ersten Mediane (d.h. am Graphen der identischen Funktion
x ® x)
hervor. Dieser Spiegelung entspricht die Vertauschung der Rollen der beiden Koordinaten, und genau das
drückt (15) für die Ableitungen aus.
Beispiel: Wir differenzieren die Wurzelfunktion
f(x) =
x1/2. Deren Inverse ist durch
x( f ) =
f 2 gegeben.
(Um sie zu erhalten, haben wir einfach die Gleichung f =
x1/2 nach x gelöst.
Die Lösung x =
f 2 ist eindeutig,
da weder x noch
f negativ werden).
Die Ableitung der inversen Funktion kennen wir bereits:
dx/df =
x'( f ) =
2f.
(Lassen Sie sich nicht dadurch beirren, dass die unabhängige Variable, nach der nun
differenziert wird, f heißt!)
Nach (15) ist die Ableitung der Wurzelfunktion daher
df /dx =
f '(x) = 1/(2f ) = 1/(2x1/2),
wobei wir im letzten Schritt wieder f =
x1/2
gesetzt haben. Das Endresultat lautet:
f '(x) = (1/2) × x-1/2.
Dank dieser sechs Ableitungsregeln können auch Funktionen, die durch komplizierte Terme
gegeben sind, relativ einfach differenziert werden, vorausgesetzt, die Ableitungen
der "Bausteine", aus denen sie zusammengesetzt sind, sind bekannt. Für diese
muss auf Formel (4) zurückgegriffen werden.
Wir wollen in diesem Abschnitt noch ein letztes Beispiel betrachten: Um die Funktion
x ® x4
zu differenzieren, haben wir vier Möglichkeiten, wobei wir die Ableitungen
(x2) ' = 2x
und
(x3) ' = 3x2
bereits oben berechnet haben und daher als bekannt voraussetzen dürfen:
- Rückgriff auf Formel (4).
- x4 als Produkt
x2 × x2
auffassen und die Produktregel (12) anwenden.
- x4 als Produkt
x3 × x
auffassen und die Produktregel (12) anwenden.
- x4 als (x2)2,
d.h. als Verkettung
f(g(x)) mit
f(g) = g2
und
g(x) = x2
auffassen und die Kettenregel (14) anwenden.
Wir werden auf die Ableitungen von Potenzfunktionen im nächsten Abschnitt eingehen, aber
als Übungsaufgabe empfehlen wir Ihnen an dieser Stelle, alle vier Methoden durchzurechnen und
sich davon zu überzeugen, dass sie zum gleichen Ergebnis
führen.
| | | |
| |
| | |
Eine sehr nützliche Methode, Ableitungen zu berechnen, das so genannte implizite Differenzieren,
müssen wir auf ein späteres Kapitel verschieben, da wir die dafür nötige
"partielle Ableitung" noch nicht kennen.
|
| | |
implizites Differenzieren
(in Vorbereitung)
| |
| | |
| Ableitung spezieller Funktionen |
| | | |
Zum Seitenanfang | |
| | |
Wir kommen nun zu den Ableitungen wichtiger spezieller Funktionen.
Zusammen mit den oben besprochenen Ableitungsregeln
bietet dieser Abschnitt das Rüstzeug für das Differenzieren der wichtigsten in der Mathematik
auftretenden Funktionen.
Funktionen, die nicht zu ihrem Lernstoff gehören, überspringen
Sie einfach!
Potenzfunktionen
Bereits oben haben wir die Ableitungen
(x2) ' = 2x
und
(x3) ' = 3x2
berechnet, als Anwendungsbeispiel von (13) das Resultat
(1/x) '
º (x-1) '
= -1/x2
und als Anwendungsbeispiel von (15) die Regel
(x1/2) ' = (1/2) × x-1/2
erzielt.
Eines der besonders schönen Resultate der Differentialrechung besteht darin, dass die
Ableitungen aller Potenzfunktionen durch eine einzige Formel beschrieben werden können:
| | | |
Potenzfunktionen
| |
| | |
Sie gilt für alle reellen Werte von n.
Damit kennen wir mit einem Schlag auch die Ableitungen von Funktionen wie
1/x2 ( = x-2)
und x-1/2
( = 1/x1/2).
Wir greifen einige interessante Fälle heraus:
| Funktion |
Ableitung |
| 1 |
0 |
| x |
1 |
| x2 |
2x |
| x3 |
3x2 |
| x4 |
4x3 |
|
|
|
|
|
|
|
|
|
|
|
| Funktion |
Ableitung |
| x1/2 |
|
| x-1/2 |
|
| identisch
mit: |
|
|
|
|
|
|
|
| | | |
| |
| | |
Die Definitionsbereiche der Ableitungen lassen sich unmittelbar daraus ablesen.
So ist beispielsweise die Wurzelfunktion
x ® x1/2
für alle
x ³ 0
definiert, während deren Ableitung
x ® (1/2) × x-1/2
nur für
x > 0
definiert ist. An der Stelle 0
ist die Ableitung von
x1/2
offensichtlich nicht definiert (denn der Term
x-1/2 reduziert sich
für x = 0
auf den sinnlosen Ausdruck 1/0).
Der Grund dafür ist am Graphen der Wurzelfunktion abzulesen: Er besitzt an dieser Stelle eine
zur y-Achse parallele
("vertikale") Tangente, und für diese lässt sich klarerweise kein (endlicher) Anstieg
angeben.
| | | |
Graph der
Wurzelfunktion
| |
| | |
Polynomfunktionen
Die Berechnung der Ableitung einer Polynomfunktion können Sie mit Hilfe der oben besprochenen Ableitungsregeln
auf die Ableitung von Potenzfunktionen, d.h. auf die Regel (16) zurückführen.
Um die Graphen der ersten und zweite Ableitung von Polynomfunktionen dritten Grades zu betrachten
und zu untersuchen, wie sie von den Koeffizienten abhängen, rufen Sie das nebenstehende Applet auf.
| | | |
Applet
Erste und zweite
Ableitung
| |
| | |
Winkelfunktionen
Auf wunderschöne Weise hängen die elementaren Winkelfunktionen Sinus und Cosinus
(im Bogenmaß) mit ihren Ableitungen
zusammen:
| | | |
Sinus und Cosinus
Bogenmaß
| |
| | |
| sin'(x) = cos x |
|
cos'(x) = - sin x |
|
|
| | | |
| |
| | |
Aus diesen ergeben sich mit Hilfe der Quotientenregel (13) und der Identität
sin2x +
cos2x = 1
die Ableitungen der Tangens- und Cotangensfunktion:
An den Polstellen von Tangens und Cotangens sind auch deren Ableitungen nicht definiert.
| | | |
Tangens und
Cotangens
Eigenschaften der Winkelfunktionen
| |
| | |
Inverse Winkelfunktionen
Wir fassen die Ableitungen der "Arcus-Funktionen" in einer Tabelle zusammen:
| Funktion |
Ableitung |
| asin x |
|
| acos x |
| - |
1
_______
_____
Ö 1 - x2 |
|
|
|
| Funktion |
Ableitung |
| atan x |
|
| acot x |
|
|
Auch diese Funktionen sind im Bogenmaß zu verstehen. So ist beispielsweise arcsin(-1) = -p/2
und arcsin(1) = p/2.
| | | |
inverse
Winkelfunktionen
| |
| | |
Exponentialfunktionen
In einem früheren Kapitel sind wir auf die Eulersche Zahl e,
die "natürliche Basis", gestoßen. Beim Differenzieren tritt nun ihre besondere Bedeutung für die Mathematik
klar zu Tage: Die Exponentialfunktion mit Basis e
ist identisch mit ihrer Ableitung:
| | | |
Die Eulersche Zahl e
| |
| | |
Mit exp(x) =
ex
können wir das auch als
exp'(x) = exp(x)
schreiben. In Wachstumsprozessen tritt oft ein Term der Form
ekx
auf. Dessen Ableitung berechnet sich mit Hilfe der Kettenregel (14) zu
| | | |
| |
| | |
Die Ableitung der Exponentialfunktion mit beliebiger Basis a
ergibt sich zu
Auch dies bezeugt die ausgezeichnete Stellung der Zahl e:
Selbst wenn man beschließt, sie nicht zu beachten, tritt in dieser Formel ganz automatisch der natürliche Logarithmus
(d.h. der Logarithmus zur Basis e) auf!
| | | |
Umrechnen v. Basen
| |
| | |
Hyperbel- und Areafunktionen
Die Ableitungen der Hyperbelfunktionen sind:
| Funktion |
Ableitung |
sinh x
|
cosh x |
cosh x
|
sinh x |
|
|
| Funktion |
Ableitung |
| tanh x |
1
cosh2x |
| coth x |
|
|
| | | |
Hyperbelfunktionen
| |
| | |
Deren Inverse, die "Areafunktionen", haben folgende Ableitungen:
| Funktion |
Ableitung |
| asinh x |
|
| acosh x |
|
|
|
| Funktion |
Ableitung |
| atanh x |
|
| acoth x |
|
|
Bis auf einzelne Vorzeichen erinnern die Ableitungen der Hyperbel- und Areafunktionen
an jene der Winkel- und Arcusfunktionen (s.o.).
| | | |
Areafunktionen
| |
| | |
Logarithmen
Ein weiterer Hinweis auf die Bedeutung der Eulerschen Zahl e ergibt
sich aus der Ableitung des natürlichen Logaritmus:
| | | |
Logarithmus
| |
| | |
Da die Logarithmusfunktion für negative Argumente nicht definiert ist, wird statt dessen
manchmal die Funktion
x ®
ln |x|
betrachtet. Sie ist für alle
x ¹ 0
definiert, und ihre Ableitung ist ebenfalls 1/x.
Der Logarithmus zu einer beliebigen Basis a
besitzt die Ableitung
In ihr tritt, ähnlich wie in (23), automatisch der natürliche Logarithmus auf, selbst
wenn zuvor von der Zahl e gar nicht die Rede war!
| | | |
Umrechnen v. Basen
| |
| | |
Mit den in diesem Abschnitt wiedergegebenen Ableitungen und den weiter oben besprochenen Ableitungsregeln
sollten Sie in der Lage sein, die meisten termdefinierten Funktionen zu differenzieren,
insbesondere beliebige Polynom- und rationale Funktionen.
Beispiel 1:
| ( |
1
(2x4 + 1)3 |
) |
' |
= - |
24x3
(2x4 + 1)4 |
|
|
(26) |
Dabei wurden (10), (11), zweimal (16) und
die Kettenregel (14) verwendet. Führen Sie die Rechnung selbst durch!
| | | |
Polynome und
rationale Funktionen
| |
| | |
Beispiel 2:
Frage: Welche Regeln wurden benutzt, um diese Ableitung zu berechnen?
Auf einige weitere Funktionen, die vom Standpunkt des Differenzierens größere Sorgfalt
erfordern, werden wir im zweiten Differenzieren-Kapitel zu sprechen
kommen.
|
| | |
Differenzieren 2
| |
| | |
| Monotonie, Extrema und Wendepunkte |
| | | |
Zum Seitenanfang | |
| | |
Falls die Ableitung einer Funktion f in jedem Punkt eines Intervalls existiert und positiv (negativ)
ist, so ist f in diesem Intervall
streng monoton wachsend (fallend). Intuitiv leuchtet das ein, da die Tangente an den Graphen in jedem
Punkt ansteigt (abfällt),
und wir verzichten hier auf einen formalen Beweis.
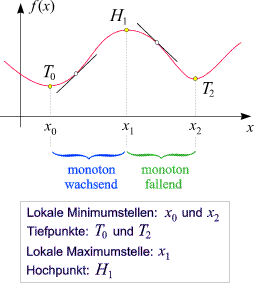
Von besonderer Bedeutung sind jene Stellen, an denen sich das Monotonieverhalten ändert:
- Ist die Ableitung innerhalb eines Intervalls für x < x0
positiv und für x > x0
negativ, und gilt
f '(x0) = 0,
so heißt x0
lokale Maximumstelle. Der entsprechende Punkt
(x0, f(x0)
am Graphen heißt Hochpunkt.
- Ist die Ableitung innerhalb eines Intervalls für x < x0
negativ und für x > x0
positiv, und gilt
f '(x0) = 0,
so heißt x0
lokale Minimumstelle. Der entsprechende Punkt
(x0, f(x0)
am Graphen heißt Tiefpunkt.
Lokale Minimum- und Maximumstellen werden unter dem gemeinsamen Namen lokale Extremstellen (oder kurz lokale Extrema)
zusammengefasst. An den entsprechenden Punkten besitzt der Graph eine horizontale Tangente
(Anstieg 0).
Der Zusatz "lokal" bezieht sich darauf, dass der Funktionswert an der
betrachteten Stelle größer (kleiner) ist als an
allen (genügend nahen) Nachbarstellen.
Irgendwo außerhalb des betrachteten Intervalls können durchaus noch größere (kleinere)
Funktionswerte auftreten. Daher kann eine Funktion mehrere lokale Extremstellen
(mit gleichen oder unterschiedlichen Funktionswerten) besitzen.
Bei den Hoch- und Tiefpunkten handelt es sich,
bildlich gesprochen, um lokale Gipfel- und die Talpunkte des Graphen.
Bemerkung: Ist
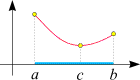eine Funktion nicht für alle reellen Zahlen definiert, so
können lokale Extrema auch an den Randstellen ihres Definitionsbereichs
auftreten. Dort muss allerdings die Ableitung nicht 0 sein.
So sei beispielsweise die Funktion, deren Graph rechts gezeigt ist, im (blau gekennzeichneten) abgeschlossenen Intervall
[a, b]
definiert. Dann besitzt sie sowohl an der linken Randstelle a
als auch an der rechten Randstelle b je ein
lokales Maximum und im Inneren des Intervalls, an der Stelle c, ein lokales Minimum.
Die Ableitungen an den Randstellen sind nicht 0,
da die Tangenten an den Graphen dort nicht horizontal sind.
Bei der Suche nach lokalen Extrema einer gegebenen Funktion sollte man daher immer die Möglichkeit
erwägen, dass sich an den Randstellen des Definitionsbereichs welche befinden.
Aus f '(x0) = 0
folgt nicht automatisch, dass x0 eine lokale
Extremstelle ist. So verschwindet beispielsweise die Ableitung der Funktion
x ® x3
an der Stelle
x0 = 0.
Sehen Sie sich Ihren Graphen (z.B. mit dem Funktions-Plotter) an!
Eine solche Stelle heißt Sattelstelle (und der entsprechende Punkt am Graphen heißt Sattelpunkt).
| | | |
Monotonie
| |
| | |
Um also (von möglichen Randstellen abgesehen) die Extremstellen einer gegebenen (differenzierbaren) Funktion f zu ermitteln, muss
- die Ableitung f ' berechnet und
- die Gleichung f '(x0) = 0
gelöst werden.
- Die Lösungen (d.h. die Zahlen x0,
für die f '(x0) = 0 gilt)
sind Kandidaten für Extremstellen. Welche von ihnen tatsächlich lokale Maxima oder Minima
darstellen, muss dann noch extra entschieden werden. Wir werden dieses Thema
im Kapitel über
Anwendungen der Differentialrechung wieder aufnehmen.
| | | |
Kriterien für lokale Extrema
| |
| | |
Besitzt die
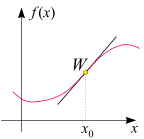Ableitungsfunktion f '
selbst wieder eine Ableitung (die zweite Ableitung f ''),
so wird eine lokale Extremstelle von f '
als Wendestelle von f bezeichnet,
der zugehörige Punkt am Graphen von f als Wendepunkt.
An einer Wendestelle x0 gilt
f ''(x0) = 0.
An ihr besitzt die Ableitung f ' ein
lokales Maximum (Minimum), d.h. an Punkten x
nahe x0 ist
f '(x) kleiner (größer) als
f '(x0).
Bildlich ausgedrückt: An einem Wendepunkt ist der Graph "am steilsten" bzw. "am wenigsten steil".
Sein Name rührt daher, dass sich an ihm die Tangente von einer Seite des Graphen auf die andere
"wendet". (Die Tangente im Wendepunkt heißt daher auch Wendetangente).
Kandidaten für Wendepunkte einer gegebenen Funktion f
sind die Lösungen der Gleichung
f ''(x0) = 0
(d.h. die Zahlen x0,
für die f ''(x0) = 0 gilt).
Handelt es sich bei einem solchen x0 tatsächlich um einen Wendepunkt, so ist
f '(x0) der Anstieg der Wendetangente.
Wir belassen es hier bei dieser kurzen Begriffsvorstellung. Weiterführendes über Extrema und Wendestellen
werden wir im Kapitel über Anwendungen sagen.
|
| | |
lokale Extrema
*
Wendestellen
| |
| | |
| Die Ableitung als Änderungsrate |
| | | |
Zum Seitenanfang | |
| | |
Die Ableitung einer Funktion f an der Stelle
x0 kann als
Änderungsrate von f
an der Stelle x0,
d.h. als Änderung des Funktionswerts pro
kleiner ("infinitesimaler") Änderung des Arguments x
in der Nähe der Stelle x0 interpretiert werden:
Ist Dx sehr klein, so gibt der
Differenzenquotient ungefähr die Ableitung an:
Df /Dx » f '(x0).
Wir schreiben diese Beziehung als
|
Df º
f(x0 + Dx)
-
f(x0)
» f '(x0) Dx . |
|
(28) |
Sie gilt umso genauer, je kleiner Dx ist.
(Anstelle von
Dx und Df
werden in diesem Zusammenhang auch die Bezeichnungen
dx und df
oder
dx und df
verwendet. Die griechischen Buchstaben
D und d
- Delta und delta -
werden in der Mathematik oft als "Änderung von" gelesen). In Worten:
Ändert sich x um Dx,
so ändert sich f ungefähr
um f '(x0) Dx.
Die Änderung Dx
spielt dabei die Rolle des oben in (1) und (4) verwendeten e.
Derselbe Zusammenhang kommt auch in den Schreibweisen (9) zum Ausdruck.
Der Differenzenquotient (1) kann als mittlere Änderungsrate
im Intervall [x0, x0 + e]
interpretiert werden. In diesem Sinn ist die Änderungsrate an einer Stelle der Grenzwert der
mittleren Änderungsrate für gegen 0 strebende
Intervallgröße.
Für eine lineare Funktion f (deren Graph eine Gerade ist)
gilt in (28) das Gleichheitszeichen. Das wirft ein weiteres Licht auf den Begriff der
Ableitung: Sie entspringt der Idee, eine gegebene Funktion an einer Stelle
durch eine lineare Funktion (deren Graph eine Gerade ist) bestmöglich zu approximieren.
Die Änderungsrate einer Funktion ist definiert als die Änderungsrate dieser
"bestmöglichen" linearen Funktion (oder, ins Geometrische übersetzt: als Anstieg der Tangente
an den Graphen).
Beispiel: Wir betrachten die Funktion
f(x) = x2 - x.
An der Stelle x0 = 3
hat sie den Wert 6, d.h.
f(3) = 6.
Aufgabenstellung: Man benutze (28), um f(3.001) näherungsweise
zu berechnen!
Wir berechnen die Ableitung
f '(x) = 2x - 1,
daher f '(3) = 5.
Nun ändert sich das Argument von
3 auf 3.001,
d.h. um Dx = 0.001.
Mit (28) ergibt sich die zugehörige Änderung des Funktionswerts zu
Df » 5 × 0.001,
woraus folgt:
f(3.001) » 6 + 5 × 0.001 = 6.005.
Vergleichen Sie dieses Ergebnis mit dem exakten Wert von f(3.001) !
(Benutzen Sie etwa den Mini-Rechner
oder JavaCalc).
Mit Hilfe der nebenstehenden Flash-Animation können Sie zur Übung die Ableitung der Funktion
f(x) = x2
an verschiedenen Stellen als Änderungsrate (Differenzenquotient) näherungsweise "messen".
| | | |
Flash
Ableitungen messen
| |
| | |
Eine Bemerkung noch zur Bezeichnung Rate. Eine "Rate" erkennt man an der Verwendung des Wortes "pro" oder
an der Formulierung "bezogen auf". So ist beispielsweise die Geschwindigkeit die Änderung des Ortes
bezogen auf die benötigte Zeit (man kann auch sagen: die Änderung des Ortes pro Zeiteinheit oder pro Sekunde).
Geschwindigkeit ist daher die (zeitliche) Änderungsrate des Ortes.
Beschleunigung (die zweite Ableitung des Ortes nach der Zeit) ist die
(zeitliche) Änderungsrate der Geschwindigkeit.
Achtung: Die Bezeichnungsweise ist nicht ganz einheitlich, was den Begriff der "Rate" betrifft.
Der nebenstehende Button ruft einige Bemerkungen hierzu (anhand der
Wachstumsrate exponentieller Prozesse) auf.
|
| | |
Zum Begriff der
| |
| | |
| Computer können differenzieren |
| | | |
Zum Seitenanfang | |
| | |
Um eine termdefinierte Funktion zu differenzieren, müssen lediglich die Ableitungen ihrer
Bestandteile bekannt sein. Der Rest ergibt sich aus der Anwendung einiger Ableitungsregeln,
die wir oben zusammengestellt haben. Der ganze Prozess geschieht gewissermaßen
nach Kochrezept, kann also von Computerprogrammen, insbesondere von
Computeralgebra-Systemen
(z.B. Mathematica,
Maple,
DERIVE,
TI-92 und
TI-89/Voyage 200)
übernommen werden.
Im Rahmen des an der Vanderbilt University zur Verfügung gestellten
MathServ Project
finden Sie das auf Mathematica beruhende Online-Werkzeug
wobei Sie unter "Number of Derivatives" eingeben können, bis zur wievielten (höheren) Ableitung gerechnet
werden soll, sowie zahlreiche weitere Programme, die zur Lösung verschiedener Probleme
Funktionen differenzieren. Sie können sie verwenden, um
Versuchen Sie aber trotz dieser Hilfen, das händische Differenzieren ein bisschen zu üben, damit Sie
wissen, was diese Programme machen.
|
| | |
| |
| | |
| | | |
Zum Seitenanfang | |
| | |
Zahlreiche Methoden der modernen Mathematik (und der meisten Anwendungsgebiete, allen voran
der Physik) bauen auf der Differentialrechnung auf. Wir werden ihr in zahlreichen
späteren Kapitel begegnen, wovon wir hier nur einige
nennen:
| | | |
| |
| | |
- In einem Kapitel, das Anwendungen der Differentialrechnung gewidmet ist,
wird es vor allem um Methoden zur Analyse von Funktionen ("Kurvendiskussion"),
zum Auffinden von Extremstellen ("Extremwertaufgaben") und zum Lösen von Gleichungen
gehen.
- Mit Hilfe der Differentialrechnung ist es möglich, Funktionen als "Potenzreihen" zu
approximieren. Damit stehen mächtige Analyse- und Berechnungsverfahren zur
Verfügung. Beispiel:
ex
= 1 + x + x2/2 + x3/6 + ...
- Im zweiten Differenzieren-Kapitel werden wir die theoretischen Konzepte der Differenzierbarkeit von
Funktionen und der Ableitung genauer formulieren und weiterentwickeln.
- Auch Funktionen in mehreren Variablen können differenziert werden.
Berechnen Sie die Ableitung der Funktion
f(x, y)
= x2 - y2
nach x
(d.h. behandeln Sie y als Konstante)!
Damit haben Sie eine partielle Ableitung berechnet. Vielleicht haben Sie den Ausdruck
"Gradient" schon gehört (zum Beispiel im Wetterbericht). Er ist ein Vektor, dessen Komponenten partielle Ableitungen sind.
Mehr darüber in einem späteren Kapitel.
- Gibt es eine Funktion f, deren Ableitung gleich ihrem Quadrat ist,
d.h. für die
f '(x)
= f(x)2 gilt? Wenn es Ihnen gelingt, eine zu finden
(mit ein bisschen Probieren ist das gar nicht so schwer), haben Sie
eine Differentialgleichung gelöst. Die Dynamik zahlreicher Systeme
(vom freien Fall eines Körpers bis zur Expansion des Universums)
lässt sich mit Hilfe solcher Gleichungen modellieren.
| | | |
Anwendungen der
Differentialrechnung
*
Potenzreihen
*
Differenzierbarkeit
*
Partielles
Differenzieren
(in Vorbereitung)
Differential-
gleichungen
(in Vorbereitung)
| |
| | |
Darüberhinaus ist die Differentialrechnung Grundlage weiterer Gebiete der Mathematik,
insbesondere der Integralrechnung, die in gewisser Weise eine
"Fortsetzung" darstellt.
Damit sind wir am Ende dieses wichtigen Kapitels angelangt.
Kehren Sie bei Bedarf später wieder zu ihm zurück, um die Ableitungen konkreter Funktionen nachzuschlagen,
Berechnungsmethoden zu wiederholen und Ihr Verständnis zu vertiefen.
|
| | |
Integralrechnung
| |