|
|
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Fast alle Zahlen, die in der Schulmathematik auftreten, sind reelle Zahlen. Reelle Zahlen sind schlicht und einfach einfach Dezimalzahlen, d.h. sie lassen sich durch eine Abfolge von Ziffern (d.h. Symbolen 0, 1, 2, 3, 4, 5, 6, 7, 8 und 9), einen Dezimalpunkt ("Komma" - wir verwenden die Schreibweise als Punkt, es kann aber auch ein Beistrich geschrieben werden; siehe hierzu Zahleneingaben: Dezimalpunkt oder Komma?) und ein Vorzeichen (- oder +, wobei letzteres weggelassen werden kann) darstellen. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Beispiele für reelle Zahlen sind -5 (''minus fünf''),
54.321 (''vierundfünfzig Komma drei zwei eins'')
und Zahlen, deren Dezimaldarstellung nie abbricht, mag sie nun
Die Menge aller reellen Zahlen wird mit R bezeichnet.
|  Mengen | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
In gewisser Hinsicht kann man sich eine reelle Zahl auch geometrisch vorstellen,
nämlich als einen Punkt auf einer Geraden. Dabei müssen zwei
Punkte dieser Zahlengeraden
als 0 und 1 ausgezeichnet sein. Damit kann man die Menge R der reellen Zahlen ''aufzeichnen''.
Im folgenden Diagramm sind einige reelle Zahlen (als Strichmarkierungen, damit man sie sieht)
eingezeichnet:
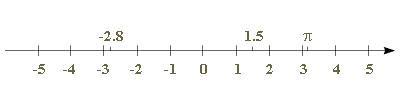
Man kann auch an ein (unendlich langes) Maßband denken, dessen Markierung so fein ist, daß sie "beliebig genaue Ablesungen" gestattet. Reelle Zahlen stellen sich nun als ''Abstand'' vom Nullpunkt (von der Nullmarkierung) dar, wobei der Punkt ''1'' gerade den Abstand 1 hat. Punkte rechts von 0 werden als positive Zahlen und Punkte links von 0 als negative Zahlen interpretiert.
Einige Teilmengen von R sind so wichtig, daß sie eigene Namen erhalten:
|  Teilmenge | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|  das Symbol \ (Komplementärmenge)  algebraische und transzendente Zahlen (in Vorbereitung) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Zahlen all dieser Mengen müssen oft als Resultat einer Berechnung angegeben werden. Eine Zahl ''angeben'' heißt, irgendeine Information angeben, die sie eindeutig festlegt. Dabei ist es sinnvoll, von vornherein die exakte Angabe einer Zahl von der Angabe eines Näherungswerts zu unterscheiden. Manchmal können reelle Zahlen recht leicht durch gewisse Eigenschaften charakterisiert werden (z.B. im Fall der Quadratwurzel aus 2, siehe unten), während die Angabe ihrer Dezimaldarstellung sehr schwer fällt. Das ist auch nicht immer nötig. So ist es etwa ziemlich überflüssig, anstelle der Zahl 1/7 die (periodische) Dezimaldarstellung 0.142857142857... anzuschreiben. Eine Angabe wie 0.142857 (ohne Punkte) ist ohnedies nicht 1/7, sondern nur ein Näherungswert. Oder, um ein anderes Beispiel anzuführen: Die Zahl p ist eine eindeutig bestimmte reelle Zahl, und 3.14 oder 3.14159 sind ebenfalls nur Näherungen, also von p verschiedene Zahlen, die nur ''ungefähr so groß sind'' wie p. In vielen mathematischen Formeln kommt die Zahl p vor, ohne daß ihre Dezimaldarstellung verwendet werden muß. Wir werden noch vielen anderen solcher Zahlen begegnen. Sie sollten der Versuchung widerstehen, jede auftretende Zahl sofort in ihre Dezimaldarstellung oder in einen Näherungswert umzurechnen. Meistens ist eine solche Methode dem Verständnis quantitativer Zusammenhänge eher abträglich als förderlich.
Im Folgenden wollen wir einige Eigenschaften dieser Zahlenmengen besprechen. Wir wollen
dabei nicht allzu rigoros vorgehen. Eine mathematisch genaue
Vorgangsweise ist übrigens ziemlich aufwendig, und das wollen wir Ihnen in diesem
einführenden Kapitel
ersparen. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Die uns vertrauteste Operation für Zahlen ist die Addition. Zwei reelle Zahlen können addiert werden, und die Summe ist wieder eine reelle Zahl, z.B.
Aus der Addition leitet sich (gewissermaßen als ''Umkehrung'') eine weitere Operation ab: die Subtraktion zweier reeller Zahlen. Wir veranschaulichen sie anhand eines Beispiels: Die Differenz
Die Subtraktion kann vollständig innerhalb der Zahlenmengen Z und Q durchgeführt werden: Die Differenz zweier ganzer (rationaler) Zahlen ist wieder eine ganze (rationale) Zahl. Aus der Menge N der natürlichen Zahlen kann die Subtraktion allerdings hinausführen: So ist etwa 3 Î N und 5 Î N, aber 3 - 5 = -2 Ï N. Die Subtraktion hängt eng mit der Tatsache zusammen, daß es Zahlen unterschiedlichen Vorzeichens gibt. Zu jeder von 0 verschiedenen reellen Zahl gibt es eine andere, die sich von ersterer nur durch das Vorzeichen unterscheidet. So bilden z.B. 7 und -7 ein Paar von Zahlen, die ''zueinander negativ'' sind. Ihre Summe ist 0. Wir bezeichnen das ''Umdrehen des Vorzeichens'' mit einem vorangestellten Minuszeichen, schreiben also z.B. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Mit dieser Definition kann jede Differenz als Summe dargestellt werden. So gilt etwa
Beachten Sie bitte beim Rechnen:
Das Minuszeichen kann insgesamt drei verschiedene Rollen spielen: in -7
ist es ein Vorzeichen (das uns sagt, daß -7 eine negative Zahl ist),
in 13 - 12 ist es ein Operationszeichen (das uns auffordert,
die beiden Zahlen zu subtrahieren), und schließlich bedeutet ein Minuszeichen vor einer
reellen Zahl, daß ihr Vorzeichen geändert werden soll. Letzteres bedeutet, auf die
reelle Zahl -7 angewandt, daß -(-7) = 7 ist!
Auf eine positive Zahl, etwa 3, angewandt, fallen die erste und die dritte Rolle
zusammen: die Zahl -3 ist natürlich jene, die aus 3 durch "Vorzeichenumdrehen"
hervorgeht. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Neben der Addition gibt es noch die Multiplikation als grundlegende Operation für reelle Zahlen. Wenn man will, kann man sie auf die Addition zurückführen, doch das ist nur für die natürlichen Zahlen leicht. So kann etwa das dreifache Addieren der Zahl 7, also
Das Verhalten negativer Zahlen in einem Produkt wird durch die Beispiele
Die Multiplikation kann vollständig innerhalb der kleineren Zahlenmengen N, N0, Z und Q durchgeführt werden: Das Produkt zweier natürlicher (ganzer, rationaler) Zahlen ist wieder eine natürliche (ganze, rationale) Zahl. Die Zahlen 0 und 1 spielen bezüglich der Multiplikation eine besondere Rolle: Die Multiplikation mit 1 ''ändert nichts'', z.B.
Aus der Multiplikation leitet sich (als ''Umkehrung'', ähnlich wie die Subtraktion aus der Addition) eine weitere Operation ab: die Division. Wir veranschaulichen sie anhand eines Beispiels: Der Quotient
Obiger Quotient kann auch als 3:2 geschrieben werden, aber wir ziehen die Schreibweise als Bruch vor (wobei die Zahl über dem Bruchstrich als Zähler, die Zahl unter dem Bruchstrich als Nenner bezeichnet wird). Weiters ist es nicht immer sinnvoll, einen Bruch sogleich in seine Dezimaldarstellung zu verwandeln. Im obigen Fall ist die Angabe 3/2 sogar für viele Zwecke günstiger als die Angabe 1.5, denn was mit 3/2 gemeint ist, ist völlig klar, während die Angabe 1.5 mitunter den Verdacht aufkommen läßt, es handle sich nur um einen Näherungswert. Außerdem läßt sich für viele Zwecke der Schulmathematik mit Brüchen besser weiterrechnen als mit Dezimalzahlen. Das Umwandeln von Brüchen in die Dezimaldarstellung sollte, falls überhaupt nötig, möglichst erst am Ende von Problemlösungen stattfinden.
Im Unterschied zur Subtraktion gibt es im Fall der Division eine extrem wichtige
Einschränkung: Die Division durch 0 ist nicht definiert!
Betrachten wir die Angelegenheit genauer:
Macht ein Quotient wie 1/0 einen Sinn?
Die zu dieser Division gehörende Fragestellung ist:
0 × wieviel = 1?
Nun haben wir oben festgestellt, daß jede Multiplikation mit 0 wieder 0 ergibt
- und daher nie 1 ergeben kann (und auch keine andere Zahl, die von 0 verschieden ist)!
Wenn die Division als ''Umkehrung'' der Multiplikation
aufgefaßt wird (wie wir es hier tun), dann ist damit schlicht und einfach nicht festgelegt
(nicht definiert), was eine Division durch 0 sein soll.
Manchmal wird das so ausgedrückt, daß die
Division durch 0 ''verboten'' ist oder daß sie keinen Sinn macht.
Auch die Frage ''Wie oft paßt 0 in 1 hinein?'' hilft hier nicht weiter - außer, daß
sie suggeriert, 1/0 sei ''unendlich'' (oder '' minus unendlich'').
Tatsächlich kann diese Lücke nicht sinnvoll ausgefüllt werden, und wir halten fest,
daß in mathematisch korrekten Ausdrücken nie eine Division durch Null
(auch nicht eine der Form 0/0) auftreten darf.
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Durch jede von Null verschiedene reelle Zahl darf dividiert werden. Wird 1
durch eine solche Zahl dividiert, so erhält man deren Kehrwert
(reziproken Wert). Beispiel:
Mit Hilfe des Kehrwerts kann ein Quotient immer als Produkt dargestellt werden. So ist z.B.
Die Division kann vollständig innerhalb der kleineren Zahlenmenge Q durchgeführt werden:
Der Quotient zweier rationaler Zahlen (mit Nenner ¹ 0) ist wieder eine rationale Zahl.
Aus den Mengen N und Z kann die Division allerdings hinausführen:
So ist etwa 3 Î N und 2 Î N, aber 3/2 = 1.5 Ï N.
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Damit haben wir die beiden algebraischen Strukturen Addition und Multiplikation
vorgestellt. Gemeinsam mit der Subtraktion und der Division werden sie als Grundrechnungsarten bezeichnet.
Was ihre grundlegenden Eigenschaften betrifft, ist nur noch zu erwähnen,
daß sie auf wunderbare Weise miteinander verwoben sind. So ist
etwa
Auf diesen Strukturen beruht der größte Teil des Schulmathematik. Wir werden allerdings in einem späteren Kapitel lernen, sie ''mit anderen Augen'' zu betrachten (nämlich in der mathematischen Symbolsprache, die erst zur Lösung anspruchsvoller Probleme befähigt). |  Variable, Terme, Formeln und Identitäten | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Ein im Rahmen der natürlichen Zahlen wichtiger Begriff ist der des Vielfachen (genauer gesagt: des ganzzahligen Vielfachen). So ist etwa 12 ein Vielfaches von 3 (nämlich das 4-fache). Umgekehrt betrachtet, ''paßt 3 genau 4 mal in 12 hinein''. Die Division 12/3 führt auf das ganzzahlige Ergebnis 4. Man sagt, ''3 teilt 12'' oder '' 3 ist ein Teiler von 12'' (bzw. ''12 wird von 3 geteilt''). All diesen Aussagen liegt die einfache Tatsache zugrunde, daß 12 = 3 × 4 ist. 5 teilt 21 nicht, da 21/5 nicht ganzzahlig ist, oder, anders ausgedrückt, da 21 kein ganzzahliges Vielfaches von 5 ist: Es gibt keine ganze Zahl n, für die 21 = 5 n wäre. Man kann aber 21 als 21 = 5 × 4 + 1 schreiben. Die hier auftretende Zahl 1 ist gerade der Rest, der sich beim Versuch, 21 durch 5 zu dividieren, ergibt. Die Teilbarkeit kann auf offensichtliche Weise auch auf negative ganze Zahlen übertragen werden (Beispiel: 3 teilt -12). Eine ganze Zahl, die von 2 geteilt wird, heißt gerade, ansonsten ungerade.
Jede natürliche Zahl besitzt sich selbst und 1 als Teiler.
Falls eine gegebene natürliche Zahl außer diesen
beiden (1 und sie selbst) keinen weiteren Teiler besitzt,
heißt sie Primzahl. So ist
beispielsweise 7 eine Primzahl, denn sie wird nicht von
2, 3, 4, 5 oder 6 geteilt, und natürlich auch nicht von einer
Zahl, die größer ist als 7.
Die ersten paar Primzahlen sind 2, 3, 5, 7, 11, 13, 17, 19, 23, ...
(1 wurde früher auch als Primzahl bezeichnet, heute aber nicht mehr).
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Längere Listen von Primzahlen können durch das ''Sieb des Eratosthenes'' erzeugt werden
(siehe den nebenstehenden Button).
Der antike Philolog, Mathematiker und Geograph Eratosthenes lebte ungefähr 275 - 195 v. Chr.
Ein Internet-Tip: Die Prime Number List erzeugt eine Liste von Primzahlen (wird in einem neuen Browser-Fenster aufgerufen). Primzahlen sind in gewisser Hinsicht die ''Bestandteile'' der natürlichen Zahlen: Jede natürliche Zahl, die größer als 1 ist, läßt sich in eindeutiger Weise als Produkt von Primzahlen schreiben. Beispiel: Die Zahl 18 kann als 2 × 9 geschrieben werden. Der Faktor 9 kann weiter als 3 × 3 zerlegt werden, woraus sich 18 = 2 × 3 × 3 ergibt. Das ist die Primfaktorzerlegung der Zahl 18: Eine weitere Zerlegung ist nicht mehr möglich, da 2 und 3 Primzahlen sind. Die Zahlen 2 und 3 heißen Primfaktoren oder Primteiler. (Der Faktor 2 kommt nur einmal vor, der Faktor 3 zweimal. Man spricht von der Vielfachheit eines Primfaktors). In der abgekürzten Schreibweise 3 × 3 = 32 (''3 zum Quadrat'', siehe unten) lautet die Primfaktorzerlegung von 18 also
Es kann streng bewiesen werden (doch wir ersuchen Sie hier, uns zu glauben), daß es für jede natürliche Zahl nur eine Primfaktorzerlegung gibt (d.h. daß sie eindeutig ist).
Ein Internet-Tip: Die
Prime Factorization Machine zerlegt natürliche Zahlen, die Sie eingeben, in ihre Primfaktoren
(wird in einem neuen Browser-Fenster aufgerufen).
Zwei (oder mehr) natürliche Zahlen können einen oder mehrere gemeinsame Teiler
besitzen.
Ist dies nicht der Fall, so heißen sie teilerfremd (oder relativ prim).
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Manchmal ist es notwendig,
den größten gemeinsamen Teiler (abgekürzt ggT)
oder das
kleinste gemeinsame Vielfache (abgekürzt kgV)
zweier (oder mehrerer) gegebener natürlicher Zahlen zu ermitteln.
Der ggT spielt etwa beim Kürzen von Brüchen,
das kgV beim Addieren von Brüchen eine Rolle.
(Beides wird weiter unten behandelt).
Hier ist die Primfaktorzerlegung hilfreich.
Falls Sie die entsprechenden Verfahren nicht kennen oder wiederholen wollen,
dann rufen Sie mit Hilfe der beiden nebenstehenden Buttons je ein Beispiel dazu auf.
Primzahlen haben seit langer Zeit die Menschen fasziniert. Einerseits gehören sie zu den am einfachstenden zu definierenden mathematischen Objekten, andererseits sind viele Fragen, die ihre Eigenschaften betreffen, bis heute ungelöst. Insbesondere das Auffinden sehr großer Primzahlen ist besonders schwierig. So werden laufend neue Rekorde gemeldet: Die im Mai 2002 größte bekannte Primzahl ist
Internet-Tip: Reaching new heights with new Mersenne prime! (Der jeweils neueste Stand ist unter dieser Adresse zu erfahren). | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Seit der Antike ist bekannt, daß es unendlich viele Primzahlen gibt.
Wenn Sie wissen wollen, wie diese Aussage vom griechischen Mathematiker Euklid
(ca. 300 v. Chr.) bewiesen wurde, dann klicken Sie auf den nebenstehenden Button.
Wir wissen aber bis heute nicht, ob es unendlich viele "Primzahlzwillinge" (wie 11, 13 oder 17, 19 oder 29, 31) gibt, um nur eine der vielen offenen Fragen zu nennen.
Im Internet gibt es eine große Zahl von Seiten, die sich mit Primzahlen
beschäftigen. (Siehe die Kategorie
Mathematische Einzelthemen > Zahlen
unserer Ressourcensammlung Mathe-Links und Online-Werkzeuge). | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Das Rechnen mit Brüchen gehorcht einfachen Regeln, die aus den Eigenschaften der Addition und der Multiplikation hergeleitet werden können. Wenn Sie mit dem Bruchrechnen noch nicht vertraut sind oder es wiederholen wollen, dann rufen Sie mit Hilfe des nebenstehenden Buttons einen kleinen Exkurs zum Thema auf. In ihm werden die wichtigsten Rechenregeln
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Von zwei verschiedenen reellen Zahlen ist immer eine kleiner als die andere (die andere also größer als die erste). In der Vorstellung der reellen Zahlen als Zahlengerade (siehe oben) ergibt sich das intuitiv: Eine Zahl ist kleiner als eine andere, wenn sie weiter links liegt. So ist etwa -5 kleiner als 3 (und daher 3 größer als -5), was auch als
Der Rest dieses Abschnitts kann von ''EinsteigerInnen'' ausgelassen werden. Diese Symbole sind wichtig, wenn Teilmengen von R - der Menge aller reellen Zahlen - beschrieben werden sollen. So ist etwa
Zusammenhängende Teilmengen von R (d.h. der Zahlengeraden) heißen Intervalle. Man bezeichnet sie mit Klammern ( ) [ ] und unterscheidet offene Intervalle (wenn die Randpunkte nicht dazugehören), z.B.
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Der Absolutbetrag (kurz Betrag) einer reellen Zahl ergibt sich, wenn das Vorzeichen auf + gestellt wird. Er wird mit dem Symbol | | bezeichnet. Beispiele: | 5.1 | = 5.1 | -7.3 | = 7.3 | p | = p | -p | = p Der Absolutbetrag von 0 wird 0 gesetzt: | 0 | = 0.
Auf der Zahlengeraden ist der Absolutbetrag der (immer ³ 0 genommene) Abstand einer
Zahl vom Nullpunkt. Eine Größe wie | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Potenzen sind zunächst einfach eine abgekürzte Schreibweise für die mehrfache Multiplikation einer reellen Zahl mit sich selbst. So ist
Aus den Rechenregeln für die Multiplikation folgt, daß 02 = 03 = ... 0 ist. (Über die Frage, ob für 00 ein konkreter Zahlenwert festgelegt werden soll, gab es früher eine Kontroverse – heute sieht man 00 als "unbestimmt" an, ähnlich wie 0/0). Zwei Beispiele für Potenzen negativer Zahlen sind
Daraus folgt folgender - besonders wichtiger - Tatbestand: Potenzen (insbesondere von irrationalen Zahlen) können nicht immer so einfach ''ausgerechnet'' werden wie in den obigen Beispielen. So ist z.B. p2 wieder eine irrationale Zahl, die man am besten so stehen läßt (sie ist näherungsweise 9.8696), und sie ist genau dieselbe Zahl wie (-p)2. Die Potenz eines Bruchs wird berechnet, indem Zähler und Nenner zur Potenz erhoben werden:
In all diesen Beispielen ist die Hochzahl eine natürliche Zahl (oder 0).
Wir wollen abschließend noch kurz erwähnen, daß auch negative Hochzahlen
gebräuchlich sind. Die Hochzahl -1 bezeichnet den Kehrwert, z.B.
5-1 = 1/5 , die Hochzahl -2
bezeichnet das Quadrat des Kehrwerts, z.B.
5-2 = 1/25 , usw.
Auch nicht-ganze Hochzahlen sind möglich, z.B.
1/2 . (Was 161/2 bedeuten soll, erwähnen
wir unten).
Wir werden uns in einem späteren Kapitel ausführlich damit
beschäftigen. |  negative Hochzahlen | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Bisher haben wir genau genommen nur über Rechenregeln gesprochen. Nun wollen wir uns zum ersten Mal einer "richtigen" mathematischen Problemstellung zuwenden. Betrachten wir eine positive reellen Zahl. Gibt es eine reelle Zahl, deren Quadrat gleich der gegebenen Zahl ist? Leichtes Beispiel: Wir beginnen mit der Zahl 4. Gibt es eine reelle Zahl, deren Quadrat 4 ist? Es gibt sogar zwei, nämlich -2 und 2. Die positive der beiden wird als die Wurzel (oder Quadratwurzel) aus 4 bezeichnet:
Schwierigeres Beispiel: Gibt es eine reelle Zahl, deren Quadrat 2 ist? Wir wollen keinen strengen mathematischen Beweis führen, sondern eher gefühlsmäßig argumentieren: Da 12 = 1 < 2 ist, ist 1 ''zu klein'', um als Ö2 in Frage zu kommen. Erhöhen wir ein bißchen: 1.012 = 1.0201 < 2, daher ist 1.01 auch zu klein. Stellen wir uns viele kleine Erhöhungsschritte vor. Sind wir bei 1.5 angelangt, so sagt uns die Rechnung 1.52 = 2.25 > 2, daß wir bereits übers Ziel hinausgeschossen haben: Die Zahl 1.5 ist zu groß, um Ö2 zu sein. Nun stellen wir uns vor, wir beginnen bei 1 und erhöhen nicht in kleinen Schritten, sondern kontinuierlich, bis der Wert 1.5 erreicht ist. (so, als ob sich ein Punkt auf der Zahlengeraden mit langsamer Geschwindigkeit, von 1 ausgehend, nach rechts bewegt, bis er 1.5 erreicht hat). Irgendwo, zwischen 1 und 1.5, wird das Quadrat der Zahl gleich 2 sein, denn zu Beginn war es zu klein, und am Ende ist es zu groß. Dahinter steht die Beobachtung, daß eine kleine Veränderung einer Zahl nur eine kleine Veränderung ihres Quadrats zur Folge hat. (Im Fachjargon heißt das, daß das Quadrieren eine stetige Operation ist). Wir kommen als zum Schuß (der sich auch streng beweisen läßt): Es gibt (genau) eine positive reelle Zahl, deren Quadrat 2 ist. Diese nennen wir die Wurzel (genauer: Quadratwurzel) aus 2 und bezeichnen sie mit Ö2. Sie liegt irgendwo zwischen 1 und 1.5. Daneben ist übrigens auch das Quadrat von -Ö2 gleich 2 (denn beim Quadrieren fällt das Minuszeichen weg). -Ö2 liegt folglich irgendwo zwischen -1.5 und 1.
Die Dezimaldarstellung von Ö2 beginnt mit 1.41421... Wenn diese Zahl exakt angegeben werden soll, muß das Symbol Ö2 verwendet werden. Es gibt keinen Grund, sie sofort durch einen Näherungswert wie 1.4142 zu ersetzen. Genau dieselbe Argumentation trifft übrigens für jede positive reelle Zahl zu: Immer gibt es zwei Zahlen (die sich nur durch das Vorzeichen unterscheiden), deren Quadrat gleich der gegebenen Zahl ist. Die positive dieser beiden Zahlen bezeichnen wir als Wurzel. Daher sind etwa die Wurzeln Ö3, Ö1.5 und Öp wohldefinierte reelle Zahlen (deren Näherungswerte Ihnen jeder Rechner mit "Wurzeltaste" oder Wurzelfunktion anzeigt). Die Zahl 0 ist ein Grenzfall: Hier gibt es nur eine Zahl, deren Quadrat 0 ist, nämlich 0 selber. Folglich schreiben wir Ö0 = 0.
Aus negativen Zahlen kann allerdings nie die Wurzel gezogen werden, da das Quadrat
jeder reellen Zahl ³ 0 ist. (Das gilt genau genommen nur im Rahmen der
reellen Zahlen. Es gibt einen allgemeineren Zahlbegriff, die ''komplexen Zahlen'',
der auch Wurzeln aus negativen Zahlen zuläßt. Er wird in diesem Kapitel
nur kurz erwähnt - siehe unten - und in einem späteren
Kapitel behandelt).
|  Komplexe Zahlen | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Nur in wenigen Fällen ist die Wurzel einer natürlichen Zahl
wieder eine natürliche Zahl. Es ist dies nur für die ''Quadratzahlen''
1, 4, 9, 16, 25, 36, 49, 64, ... der Fall.
Für alle anderen natürlichen Zahlen sieht die Lage nicht so rosig aus,
aber die Wurzeln existieren dennoch als eindeutig bestimmte reelle Zahlen.
Es läßt sich zeigen, daß sie irrational sind, d.h. daß
sie nicht als Quotient ganzer Zahlen dargestellt werden können
(oder, anders ausgedrückt, daß ihre Dezimaldarstellung weder abbricht noch periodisch ist).
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Schon in der Antike war bekannt, daß Ö2 eine irrationale Zahl ist.
(Der nebenstehende Button ruft einen Beweis dieser Tatsache auf, wie er von Euklid
überliefert wurde,
wahrscheinlich aber schon den Pythagoräern des fünften vorchristlichen
Jahrhunderts bekannt war).
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Aus Gründen, die wir später kennenlernen werden, werden Quadratwurzeln manchmal als Potenzen mit Hochzahl 1/2 angeschrieben:
Zwei nützliche Rechenregeln im Umgang mit Wurzeln sind: 1. ) Die Wurzel aus einem Produkt ist das Produkt der Wurzeln, z.B. Ö(4×9) = Ö4 Ö9 (rechnen Sie nach!). 2. ) Die Wurzel aus einem Bruch kann gezogen werden kann, indem aus Zähler und Nenner die Wurzel gezogen wird, z.B.
Zuletzt erwähnen wir anhand eines Beispiels die höheren Wurzeln: Die vierte Wurzel von 17 ist jene positive reelle Zahl, deren 4. Potenz 17 ist. Ihre Dezimaldarstellung beginnt mit 2.03054... Die dritte Wurzel wird auch Kubikwurzel genannt. |  rationale Hochzahlen | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Dieser Abschnitt kann von ''EinsteigerInnen'' ausgelassen werden. Der Vollständigkeit halber erwähnen wir hier das Stichwort Induktionsbeweis (oder Beweis durch vollständige Induktion), obwohl wir das nötige Rüstzeug, um sinnvolle Beispiele angeben zu können, hier noch nicht entwickelt haben. Kurz gesagt geht es um eine Beweismethode, die mit folgender Struktur der natürlichen Zahlen zu tun hat: Jede natürliche Zahl hat einen ''Nachfolger'', und jede natürliche Zahl wird getroffen, wenn, von 1 ausgehend, von Nachfolger zu Nachfolger gesprungen wird. Manchmal werden (in verschiedensten Teilgebieten der Mathematik) Dinge behauptet (oder vermutet) die ''für jede natürliche Zahl'' gelten sollen, und die man gerne beweisen möchte. Ein Beispiel für eine derartige Aussage ist: ''Für alle natürlichen Zahlen n gilt: Die Summe aller natürlichen Zahlen von 1 bis n ist n(n+1)/2.'' Nennen wir diese für eine natürliche Zahl n gemachte Aussage An. Falls es gelingt, zu zeigen,
bewiesen. Diese Beweismethode ist unter dem Schlagwort Induktionsbeweis gemeint.
Der nebenstehende Button ruft ein Beispiel für die Anwendung dieser Methode
(und eine lehrreiche Anekdote aus dem Leben des Mathematikers Carl Friedrich Gauß)
auf. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Dieser Abschnitt kann von ''EinsteigerInnen'' ausgelassen werden. Bisher war nur von Zahlen die Rede. Eine der genialsten Erfindungen der modernen Mathematik war die Einführung von Zahlenpaaren durch René Descartes im 17. Jahrhundert. Ein (geordnetes) Zahlenpaar besteht aus zwei Zahlen, einer ersten und einer zweiten. Sind die beiden Zahlen etwa 3 und -5, so wird das Zahlenpaar als
Zahlenpaare werden später dazu benützt werden, Punkte in einer Ebene zu beschreiben. Auch die später zu behandelnden ''ebenen Vektoren'' sind solche Objekte. Zahlentripel werden Punkte im Raum und ''räumliche Vektoren'' darstellen. |  Zeichenebene und Koordinatensystem  Vektoren 1  Analytische Geometrie 1 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Die Menge aller Zahlenpaare aus reellen Zahlen wird als R2 (gesprochen: ''R zwei''), die Menge aller Zahlentripel aus reellen Zahlen wird als R3 (gesprochen: ''R drei'') bezeichnet. (Die Menge aller reellen n-Tupel heißt dementsprechend Rn). | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Dieser Abschnitt kann von ''EinsteigerInnen'' ausgelassen werden. Er berührt tieferliegende Eigenschaften der bisher behandelten Zahlenmengen. Für den größten Teil des Stoffs der Schulmathematik ist es nicht unbedingt notwendig, die nun folgenden Dinge zu kennen, aber sie helfen, ein bißchen hinter die Kulissen zu blicken. Natürlich gibt es unendlich viele Zahlen. Das wirklich Interessante daran ist, daß zwischen verschiedenen Arten von ''unendlich'' unterschieden werden kann. Eine Menge heißt abzählbar, wenn ihre Elemente ''durchnumeriert'' werden können, d.h. wenn man jedem Element genau eine natürliche Zahl als ''Platznummer'' geben kann.
Klarerweise ist die Menge N der natürlichen Zahlen abzählbar, denn sie numeriert
sich selbst durch:
Aber auch die Menge N0 (natürliche Zahlen und 0) ist abzählbar, denn man kann sie so durchnumerieren:
Daher sind die Mengen N und N0 ''gleich groß'', denn beide lassen sich nach demselben System durchnumerieren, also auf die entsprechenden ''numerierten Plätze'' verteilen. Das mag seltsam erscheinen, denn N ist eine echte Teilmenge von N0 (sie enthält ja ein Element mehr, nämlich 0), ist aber für unendliche Mengen nichts besonderes: Gibt man zu einer unendlichen Menge noch ein Element dazu, so wird sie dadurch nicht ''größer'' !!!
Sogar die Menge Z der ganzen Zahlen
(die ja sozusagen ''mehr als doppelt so viele Elemente'' enthält als N)
ist abzählbar:
Und sogar die Menge Q der rationalen Zahlen läßt sich durchnumerieren. Man muß sich nur ein cleveres Schema überlegen, das alle Buchzahlen der Form ''ganze Zahl/ganze Zahl'' durchzählt. (Versuchen Sie es!) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Allerdings gilt das für die Menge der reellen Zahlen nicht mehr: Die
Elemente von R können nicht durchnumeriert werden
(siehe den nebenstehenden
Button für einen eindrucksvollen und vielleicht verblüffenden Beweis dieser Tatsache
- das sogenannte "Diagonalverfahren" -, der auf Georg Cantor, zurückgeht.
Cantor hat in der zweiten Hälfte des 19. Jahrhunderts
die moderne Mengenlehre mitbegründet).
Die Menge R ist also nicht abzählbar (auch überabzählbar genannt).
Offensichtlich ist sie um soviel ''größer'' als N, Z und Q, daß sie
eine andere Art von ''Unendlichkeit'' darstellt. Daraus ergibt sich übrigens, daß
auch die Menge der irrationalen Zahlen überabzählbar ist. Sie bildet den Löwenanteil
in der Menge R. Die rationalen Zahlen, mit denen man es in der Praxis so oft zu tun hat,
und die in so vielen Rechenaufgaben vorkommen, bilden
genau genommen nur eine verschwindende Minderheit!
(Man nennt sie auch ''nicht-vollständig'', da sie nicht die ganze Zahlengerade
''ausfüllen'', aber ''dicht'', da in jedem noch so kleinen Intervall
- siehe oben - rationale Zahlen liegen).
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Geht man diesen Dingen weiter auf den Grund, so stößt man auf Fragen, die sich
mit einer intuitiven (''naiven'') Sichtweise nicht
mehr beantworten lassen und die Frage aufwerfen, was Mathematik eigentlich ist, was bei
einem Beweis eigentlich geschieht, und ob die Mathematik ein vollständiges
formales logisches System bildet (oder als ein solches aufgebaut werden kann).
Der österreichische Mathematiker Kurt Gödel hat im Jahr 1931
gezeigt, daß letztere Frage verneint werden muß (zumindest, wenn nur endlich viele
Grundannahmen - "Axiome" - gemacht werden), und damit jahrhundertealte
Vorstellungen erschüttert.
Wir verfolgen dieses Thema hier nicht weiter, sondern verweisen auf ein späteres
Kapitel, in dem einige dieser Probleme wieder zur Sprache kommen
werden. |  Mathematische Strukturen und Räume (in Vorbereitung) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Dieser Abschnitt kann von ''EinsteigerInnen'' ausgelassen werden.
Die wichtigsten der bisher besprochenen Zahlenmengen sind
N, Z, Q und R. Es ist
aufschlußreich, wenn wir kurz wiederholen, welche Operationen vollständig
innerhalb dieser Mengen durchgeführt werden können:
Die Mengen Q und R stechen insofern hervor, als alle aufgezählten Operationen nicht aus ihnen hinausführen. (Solche Mengen heißen übrigens ''Körper''). Es gibt aber noch weitere Mengen, die auf einer formalen Ebene ganz ähnliche Eigenschaften haben, und die rein mathematisch erzeugt (definiert) werden können (ohne dafür ein Vorbild ''in der Wirklichkeit'' oder ''in der Natur'' zu brauchen). Ein Beispiel bildet die Menge
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Ein besonders wichtiges Zahlensystem ist durch die komplexen Zahlen C gegeben, das in einem eigenen Kapitel besprochen wird, und das R als Teilsystem enthält. Hier sei nur soviel verraten, daß ''Quadrate'' von komplexen Zahlen negativ sein können. Aber, wie im Fall der Menge (37), handelt es sich um ein eigens definiertes System, für das die Bezeichnungen ''Addition'' und ''Multiplikation'' (und daher auch ''Quadrat'') nur deshalb verwendet werden, weil diese Operationen formal ähnliche Eigenschaften wie die gleichnamigen Operationen innerhalb der reellen Zahlen besitzen. |  Komplexe Zahlen | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Obwohl es vielleicht auf den ersten Blick überraschen mag, besitzen diese Mengen, insbesondere die der komplexen Zahlen, viele nützliche Anwendungen. Es empfiehlt sich daher, den intuitiven, mit den reellen Zahlen verbundenen Zahlbegriff als einen unter vielen möglichen Zahlbegriffen aufzufassen.
Gerade die Vielzahl möglicher Zahlbegriffe illustriert den manchmal gehörten Satz,
Mathematik sei ''das Studium formaler Systeme''.
Im Internet gibt es viele Seiten, die sich mit Zahlen und Zahlensystemen beschäftigen. In diesem Zusammenhang wollen wir, neben der Kategorie Mathematische Einzelthemen > Zahlen unserer Ressourcensammlung Mathe-Links und Online-Werkzeuge, auf die Ressourcen zur Zahlentheorie des Math Forum hinweisen. Wer ein bißchen mathematischen Formalismus in Kauf nehmen will, findet viel Interessantes zu den Grundlagenfragen in den an der University of New Brunswick (Canada) zusammengestellten Frequently Asked Questions in Mathematics (Inhaltsverzeichnis). (Seiten werden in einem neuen Browser-Fenster aufgerufen). |
|
|
||
|
|
|
Zum Seitenanfang Zum Lexikon Zur Galerie Zum Inhaltsverzeichnis der Mathematischen Hintergründe Zu den interaktiven Tests Zu den Mathe-Links und Online-Werkzeugen Zur Welcome Page |