|
1.1 Back to the roots...
|

 

|
|
The purpose of this "Lernpfad" is to give a brief insight into some of the
most important and interesting theorems of Euclidean Geometry, especially
into the geometry of triangles. Before you go on the journey, make sure
that you repeat the basics about triangles. This summary (click on the word "summary"!) may help you with this!
In order NOT to cause too much needless confusion I will stick to the following nomenclature: Common Nomenclature
Have fun :-)
take notes in your portfolio, sketch triangles
|
|
1.2 Altitudes of a triangle & the orthocenter
|

|
|
Short repetition:
Draw any triangle ABC and the altitudes of the triangle with GeoGebra. What do you notice?
Don't forget to save your file!
Definition:
In Geometry, the altitudes of a triangle are the straight lines through a
vertex and which is perpenticular to (i.e. forming a right angle with)
the opposite side or an extension of the opposite side. In other words,
- it starts at a vertex and
- is perpendicular to the opposite side
Furthermore, the three altitudes intersect in a single point, called the orthocenter of the triangle.
take notes in your portfolio, repetition
|
|
1.3 Exercise - altitudes & the orthocenter
|

 

|
Click on
Assignment 1
to get your first assignment.
exercise
|
|
1.4 Experiment - Can you balance a triangle???
|

 

|
Imagine you have a triangular metal plate (or a triangular set square), and try to balance it on a point - say a pencil tip. How can you do that? Is there a special point at which it will balace?
Why don't you try it out with your set square and a pencil??

|
|
1.5 Medians of a triangle & the centroid
|

|
Definition:
In Geometry, a median of a triangle is a line segment joining a vertex to the midpoint of the opposing side. These medians intersect in a single point, called the centroid.
In Physics, the centroid of a triangle is the point through which all the mass of a triangular plate seems to act. It is also known as the 'center of gravity', 'center of mass', or barycenter.
Link:
The following link may be helpful if you want to construct the centroid of a triangle only using a compass and straightedge: centroid of a triangle
Exercise:
Click on Assignment 2 to get your next assignment.
take notes in your portfolio, exercise
|
|
1.7 Perpenticular bisector & circumcenter
|

  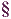
|
|
Activity:
Cut three acute scalene triangles out of paper. Make each one different! Then fold each triangle to form the perpenticular bisector of the sides (see example!). What do you observe?

Choose one triangle. Label the vertices A, B and C. Label the point of intersection of the perpenticular bisectors O. Then measure the distances AO, BO and CO. What do you observe?
Take notes in your portfolio!
Definition:
A perpendicular bisector is a line that forms a right angle with one of the triangle's sides and intersects that side at its midpoint. The three perpendicular bisectors meet in a single point, called the triangle's circumcenter. The circumcenter of a triangle is the point of concurrency of the perpendicular bisectors of the sides of a triangle. This point is the center of the circumcircle, i.e. the circle passing through all three vertices.
In general, 'to bisect' something means to cut it into two equal parts. The 'bisector' is the thing doing the cutting. With a perpendicular bisector, the bisector always crosses the line segment at right angles (90°).
Links:
The following links may be helpful for constructions only using a compass and straightedge:
activity, take notes in your portfolio, repetition
|
|
1.9 Angle bisectors & the incenter
|

  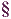
|
Definition:
An angle bisector divides the angle into two angles with equal measures. The angle bisectors of the angles of a triangle are concurrent in one single point called the incenter of the triangle, which is the center of the incircle.
In geometry, the incircle or inscribed circle of a triangle is the largest circle contained in the triangle, i.e. it touches (is tangen to) the three sides.
Links:
The following links may be helpful for constructions only using a compass and straightedge:
take notes in your portfolio
|
Lernpfadseite als User öffnen (Login)
Falls Sie noch kein registrierter User sind, können Sie sich einen neuen Zugang anlegen. Als registrierter User können Sie ein persönliches Lerntagebuch zu diesem Lernpfad anlegen.
|