|
3.1 Wichtige Eigenschaften
|

  
|
- Die allgemeine Form der Exponentialfunktion lautet: f(x) = a* b x .
- Der Parameter a wird auch Streckfaktor genannt, und b die Basis .
- Ist a negativ, wird die Kurve zusätzlich an der x-Achse gespiegelt.
- Die Graphen der allgemeinen Exponentialfunktionen enthalten die Punkte (0 | a) und (1 | b * a).
- Die allgemeine Exponentialfunktion nähert sich der x-Achse an, das heißt sie besitzt keine Nullstellen. (Da sie die x-Achse nie berührt oder schneidet.)
=> Die x-Achse bzw. die Gerade g: y = 0 ist die waagerechte Asymptote der Exponentialfunktion.
- Jeder Graf einer allgemeinen Exponentialfunktion (unabhängig von der Basis b) verläuft durch denselben Punkt P (0/1)
- Sie ist streng monoton steigend ∀x>0 und streng monoton fallend ∀x<0.
- Die Umkehrfunktion der Exponentialfunktion ist die Logarithmusfunktion.
- In der Funktionsgleichung y = a*b x +d bewirkt der Parameter d eine Verschiebung des Funktionsgraphen der allgemeinen Exponentialfunktion y = a*bx in Richtung der y-Achse .
Durch die Verschiebung nach unten kann eine Nullstelle hinzukommen.
- In der Funktionsgleichung y=a*b x+ c bewirkt der Parameter c eine Verschiebung der Exponentialkurve y = a*b x in Richtung der x-Achse.
Dieser Parameter ändert den Wertebereich jedoch nicht.
- Die Exponentialfunktion wird häufig mithilfe der Euler'schen Zahl (=e) als Basis dargestellt.
- NICHT VERGESSEN: (ex )' = ex
So sieht eine allgemeine Exponentialfunktion aus:

|
|
3.2 Durchgerechnetes Beispiel einer Kurvendiskussion
|

 
|
Kurvendiskussion der Exponentialfunktion f:
f(x) = (x-2) * e 0,5x
- Definitionsmenge:
Es gibt keine Einschränkung in der Menge der reellen Zahlen.
- Nullstellen bestimmen:
Laut Produkt-Null-Satz gilt:
f(x) = 0 ⇔
e 0,5x = 0 oder (x-2) = 0
⇒ e 0,5x = 0 existiert nicht! (Da die allgemeine Exponentialfunktion die x-Achse nur annähert, aber nie berührt)
⇒ x - 2 = 0 ⇔ x = 2
Es existiert also eine Nullstelle im Punkt N(2/0)
- Extremwerte bestimmen:
Setze f'(x) = 0
f'(x) = 0,5x * e 0,5x (ergibt sich durch Anwenden der PRODUKTREGEL)
(0,5x) * e 0,5x = 0 ⇔
0,5x = 0 ⇔
x = 0 ⇔
Wir erhalten also einen Extremwert im Punkt E(0|-2)
Um zu sehen ob es ein Hoch- oder Tiefpunkt ist, setzen wir den x-Wert in die 2. Ableitung ein.
f''(0) = 0,5 > 0
⇒ Die Funktion besitzt einen Tiefpunkt T(0|2).
- Wendepunkte bestimmen:
Setze f''(x) = 0
f''(x) = (0,25x + 0,5) * e 0,5x
0,25x + 0,5 = 0 ⇔
0,25x = -0,5 ⇔
x = -2
Um zu überprüfen ob es wirklich ein Wendepunkt ist, setzen wir x in die 3. Ableitung ein.
f'''(-2) = 0,0197 ≠ 0
⇒ Die Funktion besitzt einen Wendepunkt W(-2| -4 / e )
- Tangentensteigung:
Um die Tangentensteigung von Punkten zu bestimmen, setzen wir nun die x-Werte der Nullstellen und Wendepunkte in die erste Ableitung der Funktion ein.
f'(2) = 2,718
f'(-2) = -0,368
- Graph zeichnen:
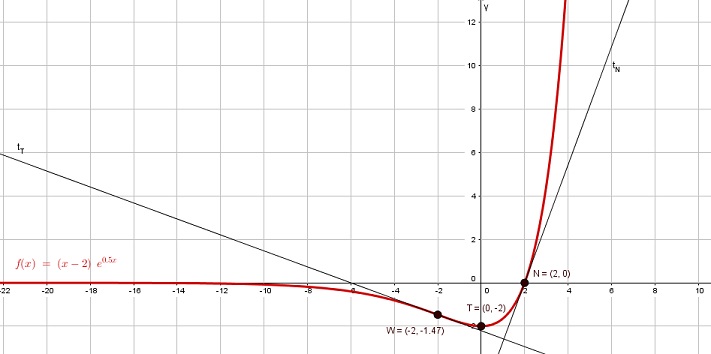
- Monotonieverhalten:
Die Funktion f ist monoton fallend im Intervall: (-∞ ; 0).
Die Funktion f ist monoton steigend im Intervall: (0 ; ∞).
- Krümmungsverhalten:
Die Funktion f ist positiv gekrümmt im Intervall: (-2 ; ∞).
Die Funktion f ist negativ gekrümmt im Intervall: (-∞ ; -2).
- Symmetrie:
Die Funktion f ist nicht symmetrisch bezüglich der y-Achse.
Beweis:
Wähle x = 2.
f(2) = 0
f(-2) = -1,472 ≠ f(2).
- Asymptotisches Verhalten:
Wie verhält sich die Funktion im Unendlichen?
lim (x→∞) [(x - 2) * e 0,5x ] = ∞ * ∞ = ∞
lim (x→ -∞) [(x - 2) * e 0,5x] = "[-∞ * 0]" → Das ist nicht definiert.
⇒ Weil die Exponentialfunktion aber streng monoton steigend ist in diesem Bereich und schneller gegen 0 strebt, als (x-2) gegen -∞, gilt:
lim (x→ -∞) [(x - 2) * e 0,5x] = 0.
Das heißt also, je größer die x-Werte, desto größer auch ihre Funktionswerte, und
je kleiner die x-Werte, desto näher sind sie zu 0.
|
|
3.3 Hausübung: Führt eine vollständige Kurvendiskussion einer Exponentialfunktion durch.
|

 

|
Nun sollt ihr euer Können beweisen!
Führt eine vollständige Kurvendiskussion der Funktion
f(x) = e 1-x²
durch.
Visualisiert den Graphen eurer Funktion bitte mit GeoGebra und ladet die Datei auf der Moodle Platform "5. Einheit" hoch.
Hier
kommt ihr direkt dort hin!
Gutes Gelingen. :)
Hausaufgabe
|
Lernpfadseite als User öffnen (Login)
Falls Sie noch kein registrierter User sind, können Sie sich einen neuen Zugang anlegen. Als registrierter User können Sie ein persönliches Lerntagebuch zu diesem Lernpfad anlegen.
|



