| | |
| | | |
| |
| | |
| Zufall und Wahrscheinlichkeit |
| | | |
| |
| | |
Nicht nur den Naturwissenschaften ist an einer möglichst genauen Beschreibung der von ihnen studierten
Phänomene gelegen. Wir alle wüssten manchmal ganz gern
über die Dinge, die uns beeinflussen, so genau Bescheid, um
präzise Voraussagen über zukünftige Geschehnisse machen zu können.
Die Natur und das Leben setzen dieser Bestrebung allerdings Grenzen.
Zufall und Zufallsexperiment
| | | |
| |
| | |
Von manchen Dingen sagen wir, dass sie zufällig geschehen. Wir meinen damit, dass
wir sie nicht mit Sicherheit vorhersehen können. Der Grund dafür kann in
schlichter Unkenntnis liegen (wen werde ich an der nächsten Straßenkreuzung treffen?)
oder aber in einer grundsätzlichen Unbestimmtheit, wie sie etwa der Freiheit menschlicher Entscheidungen
anhaftet, und wie sie nach den Erkenntnissen der Quantentheorie sogar ein grundsätzlicher Zug
"der Natur" auf physikalischer Ebene ist.
Daher sind wir oft darauf angewiesen, "ungefähre" Vorhersagen zu machen, zum Beispiel über das
Wetter im Laufe der nächsten Tage.
Wenn sich nun die Mathematik mit dem Zufall beschäftigt, so benötigt sie Modelle von Situationen,
deren Ausgang unsicher ist, und die sich mit ihren Mitteln beschreiben lassen. Derartige Modelle nennen wir (ideale) Zufallsexperimente
(oder Zufallsversuche).
Ihren grundlegenden Eigenschaften ist dieses Kapitel gewidmet.
Die anschaulichsten Zufallsexperimente stammen aus einem Bereich des Lebens, der einerseits klare
Regeln besitzt, in dem wir aber andererseits die Unsicherheit ausdrücklich wünschen:
dem Glücksspiel (das auch in der Geschichte der Mathematik der Ausgangspunkt der Wahrscheinlichkeitsrechnung
war).
Beispiel 1 eines Zufallsexperiments: Es wird ein (idealer) Würfel geworfen. Die Zusatzbezeichnung
"ideal" deutet an, dass es sich um einen absolut "fairen" Würfel handeln soll,
der jeder Augenzahl exakt die gleiche Chance gibt - eine Forderung, die zwar in der
Wirklichkeit recht gut erreicht werden kann, aber letzten Endes ein Gedankenexperiment darstellt.
Die möglichen Versuchsausgänge sind die sechs Augenzahlen: 1, 2, 3, 4, 5 und 6.
Beispiel 2 eines Zufallsexperiments: Es werden zwei unterscheidbare (ideale) Würfeln geworfen.
Wir stellen uns der Einfachheit halber vor, es handelt sich um einen roten und einen blauen Würfel.
Dabei sollen die beiden Würfeln unabhängig voneinander fallen, d.h. das Verhalten des einen
soll das Verhalten des anderen nicht beeinflussen.
Es sollen also nicht nur die Würfeln für sich genommen "ideal" sein, sondern auch deren
Unabhängigkeit wird als weiteres "ideales" Element dieses Zufallsexperiments gefordert.
Die möglichen Versuchsausgänge sind alle 36 möglichen geordneten
Paare von Augenzahlen:
(1, 1),
(1, 2),
(1, 3),
(1, 4),
(1, 5),
(1, 6),
(2, 1),
(2, 2),
(2, 3),...
(6, 4),
(6, 5) und
(6, 6).
Beispiel 3 eines Zufallsexperiments: In einer Urne befinden sich
10 rote,
15 blaue und
5 grüne Kugeln. Es wird eine Kugel zufällig ("blind") herausgegriffen.
Dabei wird wieder eine "Idealbedingung" vorausgesetzt, nämlich, dass jede der Kugeln
die gleiche Chance hat, gezogen zu werden. Weiters wollen wir zwischen Kugeln der gleichen Farbe
nicht unterscheiden.
Die möglichen Versuchsausgänge sind die 3 Farben der in der Urne enthaltenen Kugeln:
- rot (steht für: es wird eine rote Kugel gezogen)
- blau (steht für: es wird eine blaue Kugel gezogen)
- grün (steht für: es wird eine grüne Kugel gezogen)
Wie diese Beispiele zeigen, ist ein Zufallsexperiment eine gedankliche Konstruktion.
Es muss, wie andere mathematische Konstruktionen auch, "wohldefiniert" sein.
Und wie auch in anderen Gebieten der Mathematik können gedankliche Konstruktion
näherungsweise auf die Wirklichkeit angewandt werden (z.B. auf realistische Würfel,
auf eine Tombolaverlosung oder - als Beispiel eines komplexeren
Zufallsexperiments - auf das Problem der Wettervorhersage).
Jedes (ideale) Zufallsexperiment besitzt eine Menge möglicher Versuchsausgänge.
Jeder Versuchsausgang wird auch Elementarereignis genannt.
Die Menge all dieser Elementarereignisse nennen wir den Ereignisraum.
Sehen wir uns die Ereignisräume der obigen drei Beispiel an:
Beispiel 1 (Würfel): Der Ereignisraum ist die Menge der möglichen Augenzahlen {1, 2, 3, 4, 5, 6}.
Er hat 6 Elemente.
Beispiel 2 (zwei Würfeln): Der Ereignisraum ist die Menge aller geordneten Paare von
Augenzahlen
{(1, 1),
(1, 2),
(1, 3),
(1, 4),
(1, 5),
(1, 6),
(2, 1),
(2, 2),
(2, 3),...
(6, 4),
(6, 5),
(6, 6)}.
Er hat 36 Elemente.
Beispiel 3 (Urne mit Kugeln): Der Ereignisraum ist die Menge {rot, blau, grün}.
Er hat 3 Elemente.
| | | |
| |
| | |
Wir werden in diesem Kapitel nur solche Zufallsexperimente betrachten, deren
Ereignisraum endlich ist. In den nächsten Kapiteln zur Wahrscheinlichkeitsrechnung
werden auch Zufallsexperimente auftreten, deren Ereignisraum unendlich viele Elemente
besitzt.
Ereignisse und der Ereignisraum
| | | |

Wahrsch.rechnung
und Statistik
2 |
3 |
4
| |
| | |
Nun kommt ein wichtiger Begriff ins Spiel, der oft Anlass zu Missverständnissen gibt:
Ein Ereignis ist eine Zusammenfassung von Versuchsausgängen, d.h. von Elementarereignissen.
Präziser ausgedrückt: ein Ereignis ist eine Teilmenge des Ereignisraums.
Jedes Elementarereignis ist ein Ereignis, aber es gibt auch andere Ereignisse.
Sehen wir uns einige Ereignisse der drei oben betrachteten Zufallsexperimente an:
Beispiel 1 (Würfel): Mögliche Ereignisse sind
- Die Augenzahl ist 2. Das entspricht der Teilmenge {2} des Ereignisraums.
- Die Augenzahl ist eine gerade Zahl. Das entspricht der Teilmenge {2, 4, 6}
des Ereignisraums.
Beispiel 2 (zwei Würfeln): Mögliche Ereignisse sind
- Die Augenzahlen sind (1, 4).
Das entspricht der Teilmenge {(1, 4)}
des Ereignisraums.
- Beide Augenzahlen sind nicht größer als 2.
Das entspricht der Teilmenge
{(1, 1),
(1, 2),
(2, 1),
(2, 2}
des Ereignisraums.
- Die Summe der Augenzahlen ist gerade.
- Die Augenzahl des roten Würfels ist doppelt so groß wie jene des blauen Würfels.
Beispiel 3 (Urne mit Kugeln): Mögliche Ereignisse sind
- Es wird eine blaue Kugel gezogen. Das entspricht der Teilmenge {blau}
des Ereignisraums.
- Es wird eine rote oder eine blaue Kugel gezogen.
Das entspricht der Teilmenge {rot, blau}
des Ereignisraums.
Wie diese Beispiele zeigen, können Ereignisse auch verbal als "Aussagen" formuliert
werden, die eine Beschreibung ihrer Elemente darstellen. Wichtig ist, dass
jede solche Aussage eine Teilmenge des Ereignisraums eindeutig festlegt (obwohl es manchmal
schwierig sein kann, alle ihre Elemente aufzulisten).
Übung: Welche der oben angegebenen Beispiele sind Elementarereignisse, welche nicht?
Schreiben Sie das Ereignis "Die Summe der Augenzahlen ist gerade" von Beispiel 2
als Menge an! Denken Sie sich weitere Ereignisse zu diesen drei Beispielen aus!
Wird das Zufallsexperiment ausgeführt, so sagen wir, dass ein Ereignis
A
eintritt, wenn der Versuchsausgang
in der Menge A
enthalten ist. Wurde in Beispiel 1 etwa "Augenzahl 4" gewürfelt (das ist der Versuchsausgang),
so ist damit das Ereignis "Die Augenzahl ist gerade" eingetreten.
Die Ereignisse "Die Augenzahl ist 2" und "Die Augenzahl ist ungerade" sind nicht eingetreten.
Beachten Sie, dass "Versuchsausgang" und "Ereignis" nicht das gleiche ist!
Mit jedem Versuchsausgang treten gewisse Ereignisse ein und andere nicht.
| | | |
| |
| | |
Die bisher vorgestellten Begriffe (Zufallsexperiment, Versuchsausgang = Elementarereignis, Ereignisraum,
Ereignis) stecken den Rahmen ab, in dem sich die Wahrscheinlichkeitsrechnung bewegt.
Auch weiterführende Themen, auf die wir in den nachfolgenden
Kapiteln eingehen werden (z.B. das der Zufallsvariable und der Wahrscheinlichkeitsverteilung)
beziehen sich auf ihn.
Wahrscheinlichkeit
| | | |

Wahrsch.rechnung
und Statistik
2 |
3 |
4
| |
| | |
Wird die Begrenzung unserer Möglichkeiten, exakte Voraussagen zu treffen, von der Mathematik reflektiert, so stellt sich der
Wunsch ein, zumindest ein Maß für die Sicherheit (oder Unsicherheit) anzugeben, die mit einer Aussage verbunden ist.
Ein solches Maß ist die Wahrscheinlichkeit.
Die Wahrscheinlichkeitsrechnung ordnet jedem Ereignis eines Zufallsexperiments eine Wahrscheinlichkeit
für sein Eintreten zu.
Nennen wir ein Ereignis A, so wird
die ihm zugeschriebene Wahrscheinlichkeit mit
p(A) oder
pA
bezeichnet. (Der Buchstabe p
stammt vom englischen probability). Andere Bezeichnungen, die Sie in der Literatur finden, sind
P(A),
PA und
Prob(A).
Die Wahrscheinlichkeit für das Eintreten eines Ereignisses A ist immer eine reelle Zahl,
für die
gilt. Zwei Extremfälle kennzeichnen Sicherheit:
- Ist p(A) = 1, so tritt
A mit Sicherheit ein.
- Ist p(A) = 0, so tritt
A mit Sicherheit nicht ein.
Die Werte dazwischen drücken Grade an Sicherheit aus. Je größer die
Wahrscheinlichkeit p(A), umso "eher" ist anzunehmen, dass das Ereignis
A eintritt.
Was aber bedeutet das genau? Wie sind die Grade an Sicherheit, die
durch Wahrscheinlichkeiten ausgedrückt werden, definiert?
|
| | |
| |
| | |
| Wahrscheinlichkeit und relative Häufigkeit |
| | | |
Zum Seitenanfang | |
| | |
Bevor wir zur Berechnung von Wahrscheinlichkeiten kommen, müssen wir wissen,
was sie bedeuten. Gehen wir von einem der einfachsten Zufallsexperimente aus: dem
Würfel (Beispiel 1 oben).
Das Maß für die Sicherheit, die höchste Augenzahl 6 zu würfeln,
könnte vielleicht so formuliert werden: "Ungefähr bei jedem sechsten Würfel-Versuch
wird die Augenzahl 6 auftreten". Das bedeutet:
"Unter 6 Würfel-Versuchen wird ungefähr 1 mal die Augenzahl 6 auftreten".
Ganz sicher können wir natürlich nicht sein, dass bei lediglich 6 Versuchen die gewünschte Augenzahl genau einmal eintritt,
also würfeln wir öfter: "Unter 6000 Würfel-Versuchen wird ungefähr 1000 mal die Augenzahl 6 auftreten".
Das klingt schon plausibler. Gehen wir noch einen Schritt weiter:
"Unter einer sehr großen Zahl n von Würfel-Versuchen wird ungefähr
n/6 mal die Augenzahl 6 auftreten".
Nun wollen wir ein bisschen genauer sein: Wenn wir ein Zufallsexperiment in identischer Weise
n mal durchführen
und dabei genau m
mal das Ereignis A eintritt,
so nennen wir den Quotienten
| | | |
| |
| | |
die relative Häufigkeit, mit der das Ereignis A eingetreten ist.
Die relative Häufigkeit wird nicht bei jeder Reihe von n Versuchsdurchführungen
gleich sein. Wenn aber n sehr groß ist,
so wird sich jedes Mal ungefähr die gleiche relative Häufigkeit ergeben, und wenn
wir gedanklich in einem Grenzprozess
n über jede Schranke wachsen lassen,
so sollte die relative Häufigkeit einen fixen, nur vom Zufallsexperiment und dem betrachteten Ereignis A
abhängigen Wert annehmen. Diesen Wert nennen wir die Wahrscheinlichkeit des Ereignisses.
Bemerkung: Sie können die Gesetzmäßigkeit, auf die sich diese Argumentation gründet,
durch eifriges Würfeln selbst nachvollziehen.
Um es einfacher zu machen, haben wir das Würfeln einem Zufallsgenerator übertragen
und für drei Werte von n
die Anzahl des Auftretens von Augenzahl 6 in diesen n
Versuchsdurchführungen und die dazugehörige relative Häufigkeit ermittelt.
Dabei wurde jeder dieser n Versuche
5 mal durchgeführt:
| n |
Augenzahl 6 tritt so oft auf |
relative Häufigkeit |
| 6 |
1, 1, 0, 2, 0 |
0.1667, 0.1667, 0, 0.3333, 0 |
| 60 |
7, 9, 8, 10, 9 |
0.1167, 0,15, 0.1333, 0.1667, 0.15 |
| 6000 |
1046, 1026, 993, 963, 986 |
0.174, 0.171, 0.166, 0.161, 0.164 |
Sie sehen, dass die relativen Häufigkeiten, die in der dritten Spalte auftreten, mit wachsendem
n einander immer ähnlicher
werden.
Damit können wir eine Definition der Wahrscheinlichkeit formulieren:
|
Die Wahrscheinlichkeit eines Ereignisses ist die für eine gegen unendlich strebende
Anzahl n von Durchführungen des betreffenden Zufallsexperiments
vorausgesagte relative Häufigkeit seines Eintretens.
|
|
|
(3) |
Da wir n in der Wirklichkeit nicht "gegen unendlich streben"
lassen können, handelt es sich hier, wie beim Begriff des Zufallsexperiments
(siehe oben) um eine mathematische Idealisierung.
Diese Definition passt mit den beiden Eigenschaften der Wahrscheinlichkeit, die wir bereits oben besprochen
haben, zusammen:
- Die relative Häufigkeit jedes Ereignisses A erfüllt stets
0 £ h(A) £ 1,
und daher gilt dies auch für jede Wahrscheinlichkeit.
(Beweis: Tritt das Ereignis bei n-maliger Durchführung des Zufallsexperiments
m mal ein, so gilt
0 £ m £ n,
woraus die Behauptung folgt).
- Tritt ein Ereignis A mit Sicherheit ein, so tritt es bei n-maliger Durchführung des Zufallsexperiments immer,
d.h. n mal ein. Seine relative Häufigkeit ist
gleich n/n = 1, und daher ist
p(A) = 1.
- Tritt ein Ereignis A mit Sicherheit nicht ein, so tritt es bei n-maliger Durchführung des Zufallsexperiments nie,
d.h. 0 mal ein. Seine relative Häufigkeit ist
gleich 0/n = 0, und daher ist
p(A) = 0.
Mit dieser Definition sind wir nun in der Lage, zur Berechnung von Wahrscheinlichkeiten überzugehen.
|
| | |
Grenzprozesse
| |
| | |
| | | |
Zum Seitenanfang | |
| | |
Die einfachsten Zufallsexperimente sind dadurch gekennzeichnet, dass jeder Versuchsausgang
gleich wahrscheinlich ist. Wir nennen sie Laplace-Experimente.
Ein typisches Beispiel ist der (ideale) Würfel. Selbst wenn wir die Wahrscheinlichkeiten
für das Eintreten der einzelnen Augenzahlen nicht kennen, sorgt seine
perfekte (ideale) Form dafür, dass sie alle gleich groß sind. Diese Information
reicht aber aus, sie konkret zu berechnen:
Wird n mal gewürfelt,
so sagen wir für sehr großes n
und aufgrund der Gleichberechtigung der Augenzahlen voraus,
dass jede gegebene Augenzahl n/6
mal eintreten wird.
Die entsprechende Wahrscheinlichkeit ist mit (3) dann
(n/6)/n = 1/6.
Nun erinnern wir uns daran, dass Ereignisse auch komplexer sein können: Sie sind Zusammenfassungen
von Versuchsausgängen. So ist für den (idealen) Würfel auch "Die Augenzahl ist gerade"
ein Ereignis. Wie groß ist die Wahrscheinlichkeit für sein Eintreten?
Dazu überlegen wir:
Unter den 6 möglichen Augenzahlen (den so genannten möglichen Fällen)
sind 3 geradzahlig (nämlich 2, 4 und 6). Das sind die so genannten günstigen Fälle.
Jeder einzelne günstige Fall (und auch jeder einzelne ungünstige Fall) tritt bei
n-maligem Würfeln für sehr großes n
gleich oft ein, nämlich n/6 mal,
d.h. sein relativer Anteil ist 1/6.
Jetzt müssen wir nun noch zählen: Der relative Anteil der
günstigen Fälle (gerade Augenzahl) ist dreimal so groß wie der relative Anteil jeder einzelnen Augenzahl,
also 3/6 = 1/2.
Daher ist die Wahrscheinlichkeit, eine gerade Augenzahl zu würfeln, gleich
1/2.
Hinter diesem Argument steckt eine Regel, die für beliebige
Laplace-Experimente anwendbar ist und die Berechnung von Wahrscheinlichkeiten
auf das Abzählen von Fällen reduziert.
- Die Anzahl aller möglichen Versuchsausgänge eines Laplace-Experiments (d.h. die Zahl der Elemente seines
Ereignisraums) wird die "Zahl der möglichen Fälle" genannt.
Alle diese Fälle sind (für ein Laplace-Experiment) gleich wahrscheinlich.
- Sei nun A ein Ereignis.
Es besteht aus gewissen Versuchsausgängen, und deren
Anzahl wird die "Zahl der günstigen Fälle" genannt.
(Sie ist die Zahl der Elemente, die das Ereignis A
- als Teilmenge des Ereignisraums -
besitzt, oder, wiederum anders ausgedrückt, die Zahl
der möglichen Versuchsausgänge, aus deren Eintreten das Eintreten von A folgt).
Dann ist die Wahrscheinlichkeit für das Eintreten des Ereignisses A
durch den Quotienten
| p(A) |
= |
Zahl der günstigen Fälle
Zahl der möglichen Fälle |
|
|
(4) |
gegeben.
| | | |
| |
| | |
Beispiel: Um im obigen Beispiel 2 (ein roter und ein blauer Würfel)
die Wahrscheinlichkeit des Ereignisses
"Die Summe der Augenzahlen ist gerade" zu berechnen, benötigen wir
- die Zahl der möglichen Fälle (Zahl der möglichen Versuchsausgänge). Sie ist 36.
- die Zahl der günstigen Fälle, d.h. die Zahl der möglichen Versuchsausgänge,
bei denen die Summe der Augenzahlen gerade ist. Dazu müssen wir ein bisschen überlegen:
Die Summe der Augenzahlen ist gerade, wenn beide Augenzahlen gerade oder wenn beide Augenzahlen ungerade
sind. Da jeder Würfel 3 gerade und 3 ungerade Augenzahlen besitzt,
gibt es 9 Versuchsausgänge der Form (gerade, gerade)
und 9 Versuchsausgänge der Form (ungerade, ungerade).
Insgesamt gibt es also 18 günstige Fälle.
Die Berechnung ist mit (4) nun ganz einfach:
p(Die Summe der Augenzahlen ist gerade) = 18/36 = 1/2.
Um Schreibarbeit zu sparen, kann dem Ereignis ein Name gegeben werden, z.B. A,
womit also folgt: p(A) = 1/2.
Vergessen Sie nicht, dass die schöne Formel (4) nur für Laplace-Experimente
gilt. Nicht jedes Zufallsexperiment ist von diesem Typ.
Beispiel: Das obige Beispiel 3 (Urne mit 10 roten,
15 blauen und 5 grünen Kugeln,
wobei Kugeln gleicher Farbe nicht unterschieden werden und eine Kugel zufällig herausgegriffen wird) ist kein Laplace-Experiment.
Das folgt daraus, dass die Versuchsausgänge
rot, blau und grün
(für die herausgegriffene Kugel) nicht die gleiche Chance haben, einzutreten.
Es lässt sich aber leicht auf ein Laplace-Experiment zurückführen, wenn wir einen
kleinen Trick anwenden: Wir nummerieren die Kugeln (heimlich) durch, so dass jede ihre eigene
Identität besitzt. Nun wird jede Nummer mit der gleichen Wahrscheinlichkeit gezogen - wir
haben aus dem Urnenbeispiel vorübergehend ein Laplace-Experiment gemacht:
- Die Zahl der möglichen Fälle ist 30 (die Anzahl der Kugeln in der Urne).
- Hinsichtlich des Versuchsausgangs rot ist die Zahl der günstigen Fälle 10 (die Anzahl der roten Kugeln in der Urne).
- Hinsichtlich des Versuchsausgangs blau ist die Zahl der günstigen Fälle 15 (die Anzahl der blauen Kugeln in der Urne).
- Hinsichtlich des Versuchsausgangs grün ist die Zahl der günstigen Fälle 5 (die Anzahl der grünen Kugeln in der Urne).
Die Wahrscheinlichkeiten für die drei Versuchsausgänge des ursprünglichen Zufallsexperiments sind daher
- p(Es wird eine rote Kugel gezogen) = 10/30 = 1/3.
- p(Es wird eine blaue Kugel gezogen) = 15/30 = 1/2.
- p(Es wird eine grüne Kugel gezogen) = 5/30 = 1/6.
Die heimliche Nummerierung der Kugeln wird nun nicht mehr benötigt.
Durch diese drei Zahlen (die genau den relativen Häufigkeiten der drei Kugelsorten in der Urne entsprechen) lassen sich die Wahrscheinlichkeiten aller Ereignisse des Zufallsexperiments
ausdrücken (z.B. für das Ereignis, eine nicht-rote Kugel zu ziehen).
Wie das gemacht wird, werden wir im nächsten Abschnitt besprechen.
In ähnlicher Weise lassen sich viele Aufgaben der Wahrscheinlichkeitsrechnung auf Laplace-Experimente zurückführen.
Versuchen Sie, die Logik, die diesen Argumentationen zugrunde liegt, und den Anwendungsbereich der
Formel (4) möglichst genau zu verstehen!
|
| | |
| |
| | |
| Rechenregeln für Wahrscheinlichkeiten |
| | | |
Zum Seitenanfang | |
| | |
Nun wollen wir ein paar grundlegende Eigenschaften von Wahrscheinlichkeiten besprechen.
Wir gehen von einem Zufallsexperiment und dessen Ereignisraum aus. Wie
oben besprochen,
- ist der Ereignisraum - wir nennen ihn jetzt E - die Menge aller
Versuchsausgänge (oder Elementarereignisse).
- Ein Ereignis ist eine Zusammenfassung von Versuchsausgängen und kann als Teilmenge von E
angesehen werden.
| | | |
| |
| | |
Ereignisse können
in verschiedener Weise in Beziehung zueinander stehen, und ein Ereignis kann aus anderen Ereignissen
konstruiert werden. Da Ereignisse Teilmengen des Ereignisraums sind,
können ihre Beziehungen in Begriffen der Mengenlehre
ausgedrückt, und sie können wie Mengen miteinander verknüpft werden.
Wie werden nun einige dieser Verknüpfungen kennen lernen und besprechen, wie die
Wahrscheinlichkeiten der entsprechenden Ereignisse miteinander zusammenhängen.
Disjunkte Ereignisse und die Additionsregel
| | | |

Mengen
| |
| | |
Aus zwei Ereignissen A und B
(d.h. zwei Teilmengen des Ereignisraums E )
lässt sich ein drittes bilden: ihre Vereinigung
A È B.
Sie besteht als allen Versuchsausgängen, die entweder in A
oder in B enthalten sind und ist,
da A È B wieder eine
Teilmenge von E ist, ebenfalls ein Ereignis.
Wir können es als "Es tritt entweder A
oder B ein" oder kurz als
"A oder B"
bezeichnen. Eine andere Schreibweise dafür ist
A Ú B,
wobei das Symbol Ú als "oder" ausgesprochen wird.
Beachten Sie, dass
A È B = B È A
gilt. )
lässt sich ein drittes bilden: ihre Vereinigung
A È B.
Sie besteht als allen Versuchsausgängen, die entweder in A
oder in B enthalten sind und ist,
da A È B wieder eine
Teilmenge von E ist, ebenfalls ein Ereignis.
Wir können es als "Es tritt entweder A
oder B ein" oder kurz als
"A oder B"
bezeichnen. Eine andere Schreibweise dafür ist
A Ú B,
wobei das Symbol Ú als "oder" ausgesprochen wird.
Beachten Sie, dass
A È B = B È A
gilt.
| | | |

Vereinigungsmenge

logisches "oder"
| |
| | |
Wir nennen nun zwei Ereignisse A und B
disjunkt oder einander ausschließend, wenn ihr Durchschnitt
leer ist.
Beispiele:
- Im obigen Beispiel 1 (Würfel) sind die
Ereignisse
A = "Die Augenzahl ist gerade"
und
B = "Die Augenzahl ist 1 oder 3"
disjunkt.
- Im obigen Beispiel 2 (zwei Würfel) sind die
Ereignisse
A = "Beide Augenzahlen sind nicht größer als 2"
und
B = "Die Summe der Augenzahlen ist 5"
disjunkt.
- Im obigen Beispiel 3 (Urne mit Kugeln) sind die
Ereignisse
A = "Es wird eine rote Kugel gezogen"
und
B = "Es wird eine nicht-rote Kugel gezogen"
disjunkt.
Disjunkte Ereignisse können nicht gleichzeitig eintreten, d.h. bei jedem Versuchsausgang
tritt entweder A oder B
(oder keines von beiden) ein.
Die Vereinigung A ÈB zweier disjunkter Ereignisse
A und B
(die so genannte "disjunkte Vereinigung") kann in der Form
"Es tritt entweder A
oder B ein, aber nicht beide gleichzeitig"
beschrieben werden.
Für die Wahrscheinlichkeiten disjunkter Ereignisse gilt die Additionsregel
| | | |

disjunkt
| |
| | |
|
p(A oder B) º
p(A È B) º
p(A Ú B) = p(A) + p(B).
|
|
|
(5) |
In Worten: Schließen A und B einander
aus, so ist die Wahrscheinlichkeit, dass entweder A oder B
eintritt, gleich der Summe der Wahrscheinlichkeiten für A und B.
Beispiele:
- Im obigen Beispiel 1 (Würfel) sei
- A = "Die Augenzahl ist gerade".
- B = "Die Augenzahl ist 1 oder 3".
Diese beiden Ereignisse sind disjunkt, und es gilt mit (4):
- p(A) = 3/6 = 1/2.
- p(B) = 2/6 = 1/3.
Daher ist
p(A È B) = 1/2 + 1/3 = 5/6
die Wahrscheinlichkeit, dass die Augenzahl entweder gerade oder 1 oder 3 ist.
- Im obigen Beispiel 2 (zwei Würfel) sei
- A = "Beide Augenzahlen sind nicht größer als 2".
- B = "Die Summe der Augenzahlen ist 5".
Diese beiden Ereignisse sind disjunkt, und es gilt mit (4):
- p(A) = 4/36 = 1/9.
- p(B) = 4/36 = 1/9.
Daher ist
p(A È B) = 1/9 + 1/9 = 2/9
die Wahrscheinlichkeit, dass entweder beide Augenzahlen nicht größer als 2 sind
oder die Summe der Augenzahlen 5 ist.
- Im obigen Beispiel 3 (Urne mit Kugeln) sei
- A = "Es wird eine nicht-rote Kugel gezogen".
Anders ausgedrückt: A = "Es wird eine blaue oder eine grüne Kugel gezogen".
Da jede Kugel nur eine Farbe besitzt, sind die Ereignisse blau und grün disjunkt.
Ihre Wahrscheinlichkeiten haben wir bereits oben berechnet:
- p(blau) = 1/2.
- p(grün) = 1/6.
Daher ist
p(A) = p(blau oder grün) = 1/2 + 1/6 = 2/3
die Wahrscheinlichkeit, dass eine nicht-rote Kugel gezogen wird.
(Wir werden ein bisschen weiter unten eine zweite Methode kennen lernen,
diese Wahrscheinlichkeit zu berechnen).
Die Additionsregel (5) lässt sich auf mehrere Ereignisse
A1, A2, A3,...
ausdehnen, sofern sie paarweise disjunkt sind. In diesem Fall gilt für ihre
Wahrscheinlichkeiten
|
p(A1 È A2 È A3 È ...) = p(A1) + p(A2) + p(A3) + ...
|
|
(6) |
Achtung: Natürlich lässt sich auch die Vereinigung beliebiger Ereignisse bilden.
Sind sie aber nicht (paarweise) disjunkt, so gilt für sie die Additionsregel (5) bzw. (6) nicht.
Gegenwahrscheinlichkeit
| | | |
| |
| | |
Ist A ein Ereignis
(d.h. eine Teilmenge des Ereignisraums E ),
so können wir seine Komplementärmenge
E \ A
bilden, d.h. die Menge aller Versuchsausgänge, die nicht in A
enthalten sind. Da sie wieder eine Teilmenge von E
ist, ist sie ebenfalls ein Ereignis. Wir können es als "A tritt nicht ein"
oder kurz "nicht-A" bezeichnen.
Eine andere Schreibweise dafür ist
Ø A,
wobei das Symbol Ø als "nicht" ausgesprochen wird.
Es heißt auch das Gegenereignis von A
(oder die Negation von A).
Beachten Sie, dass das Gegenereignis des Gegenereignisses wieder das ursprüngliche Ereignis ist:
Ø Ø A = A. ),
so können wir seine Komplementärmenge
E \ A
bilden, d.h. die Menge aller Versuchsausgänge, die nicht in A
enthalten sind. Da sie wieder eine Teilmenge von E
ist, ist sie ebenfalls ein Ereignis. Wir können es als "A tritt nicht ein"
oder kurz "nicht-A" bezeichnen.
Eine andere Schreibweise dafür ist
Ø A,
wobei das Symbol Ø als "nicht" ausgesprochen wird.
Es heißt auch das Gegenereignis von A
(oder die Negation von A).
Beachten Sie, dass das Gegenereignis des Gegenereignisses wieder das ursprüngliche Ereignis ist:
Ø Ø A = A.
Die Wahrscheinlichkeit eines Gegenereignisses (die so genannte Gegenwahrscheinlichkeit) ist durch
| | | |

Komplementärmenge

logisches "nicht"
| |
| | |
gegeben.
Sie können sich diese Formel auch in der Form
p(A) + p(Ø A ) = 1
merken: Die Summe aus der Wahrscheinlichkeit und der Gegenwahrscheinlichkeit eines Ereignisses ist
gleich 1.
Beispiel:
- Im obigen Beispiel 3 (Urne mit Kugeln) sei
- A = "Es wird eine nicht-rote Kugel gezogen".
Wir haben seine Wahrscheinlichkeit oben mit Hilfe der Additionsregel (5)
berechnet. Eine andere Methode besteht darin, zu erkennen, dass A
das Gegenereignis zu
- B = "Es wird eine rote Kugel gezogen"
ist, dessen Wahrscheinlichkeit wir oben bereits zu 1/3 berechnet haben.
Daher ist mit (7)
- p(A) = 1 - p(B) =
1 - 1/3 = 2/3
die Wahrscheinlichkeit, dass eine nicht-rote Kugel gezogen wird (und stimmt natürlich mit dem
bereits erhaltenen Ergebnis überein).
Die Benutzung von Gegenereignissen ist ein bewährter Trick zur Abkürzung von Berechnungen,
den Sie bei konkreten Aufgaben immer erwägen sollten.
Normierung der Wahrscheinlichkeiten
| | | |
| |
| | |
Wir wenden uns nun den Versuchsausgängen (Elementarereignissen) zu.
Da je zwei Versuchsausgänge (aufgefasst als ein-elementige Teilmengen des
Ereignisraums E )
disjunkt sind, können wir ihre disjunkte Vereinigung bilden.
Diese ist der Ereignisraum selbst! Die ihm zugeordnete Wahrscheinlichkeit ist
1, da mit Sicherheit einer der möglichen Versuchsausgänge
eintritt. Nummerieren wir alle Versuchsausgänge eines Zufallsexperiments in der Form
A1, A2, A3,...
durch, so gilt mit (6) dann )
disjunkt sind, können wir ihre disjunkte Vereinigung bilden.
Diese ist der Ereignisraum selbst! Die ihm zugeordnete Wahrscheinlichkeit ist
1, da mit Sicherheit einer der möglichen Versuchsausgänge
eintritt. Nummerieren wir alle Versuchsausgänge eines Zufallsexperiments in der Form
A1, A2, A3,...
durch, so gilt mit (6) dann
|
p(A1) + p(A2) + p(A3) + ... = 1.
|
|
|
(8) |
| | | |
| |
| | |
In Worten: Die Summe der Wahrscheinlichkeiten aller Elementarereignisse ist gleich 1.
Diese Tatsache wird als Normierung der Wahrscheinlichkeiten oder Normierungsbedingung bezeichnet.
Sie ist besonders wichtig für das Rechnen mit Wahrscheinlichkeitsverteilungen,
wie wir es im nächsten Kapitel tun werden.
Beispiel: Für das obige Beispiel 3 (Urne mit Kugeln) wurden
bereits die Wahrscheinlichkeiten aller drei Versuchsausgänge
berechnet. Nun können wir ihre Normierung überprüfen:
1/3 + 1/2 + 1/6 = 1.
Die Erkenntnis (8) gibt Anlass zu zwei Bemerkungen:
| | | |

Wahrscheinlich-
keitsrechnung und Statistik 2
| |
| | |
- Da die Vereinigung aller Ereignisse in (8) gleich dem gesamten Ereignisraum ist,
drückt diese Beziehung die Tatsache aus, dass p(E) = 1
ist. (Beachten Sie: Der Ereignisraum selbst ist als Teilmenge seiner selbst ebenfalls ein Ereignis!
Da er alle Versuchsausgänge enthält, also bei jedem Versuchsausgang eintritt,
ist seine Wahrscheinlichkeit gleich 1).
- Ist A ein beliebiges Ereignis, d.h. eine
Teilmenge von E, so können wir
es uns als disjunkte Vereinigung aller ein-elementigen Mengen vorstellen, die aus seinen Elementen gebildet werden.
Aus (6) folgt dann, dass p(A)
gleich der Summe der Wahrscheinlichkeiten aller Versuchsausgänge ist, die in
A enthalten sind. Mit dieser Verallgemeinerung von
(8) kann die Wahrscheinlichkeit jedes Ereignisses aus den Wahrscheinlichkeiten
der Versuchsausgänge berechnet werden.
- Es gibt eine besondere Teilmenge des Ereignisraums, die wir noch nicht berücksichtigt haben:
die leere Menge { }.
Der Vollständigkeit halber ordnen wir ihr die Wahrscheinlichkeit
p({ }) = 0 zu.
Eine hilfreiche Vorstellung
| | | |

leere Menge
| |
| | |
Die bisher erziehlten Resultate, insbesondere die Additionsregel (5) bzw. (6) für
disjunkte Ereignisse, legen eine besonders hilfreiche Vorstellung der Wahrscheinlichkeiten von Ereignissen
nahe: Stellen Sie sich vor, jeder Versuchsausgang (d.h. jedes Element des Ereignisraums) hätte ein
"Gewicht", so dass der gesamte Ereignisraum das "Gewicht" 1 hat.
Die Wahrscheinlichkeit eines Ereignisses, d.h. einer Teilmenge des Ereignisraums, ist dann einfach das "Gewicht"
dieser Menge. (Statt an ein "Gewicht" können sie an irgendeine andere Größe
denken, wie eine "Fläche" oder einen "Volumensinhalt". Wichtig ist nur, dass die
Werte dieser Größe bei der Zusammenfassung mehrerer Elemente addiert werden, und
dass die Gesamtsumme 1 ist).
Gehen Sie zur Übung die Formeln (5), (6), (7) und
(8) unter diesem Gesichtspunkt noch einmal durch!
Die Multiplikationsregel für unabhängige Ereignisse
| | | |
| |
| | |
Betrachten wir wieder zwei Ereignisse A und
B. Aus ihnen können wir
die Durchschnittmenge
A Ç B
bilden, d.h. die Menge all jener Versuchsausgänge, die
in A und in B
enthalten sind. Da diese wieder eine Teilmenge des Ereignisraums E
ist, ist sie ebenfalls ein Ereignis. Wir können es als
"Es treten A und B
ein" oder kurz als "A und B"
bezeichnen. Eine andere Schreibweise dafür ist
A Ù B,
wobei das Symbol Ù als "und" ausgesprochen wird.
Beachten Sie, dass
A Ç B = B Ç A
gilt.
Der Durchschnitt zweier Ereignissen ist insbesondere dann von Interesse, wenn aufgrund der Definition eines Zufallsexperiments von vornherein klar
ist, dass sie statistisch voneinander unabhängig sind, d.h. dass das Eintreten des einen nichts an der Chance, dass
das andere eintritt, ändert.
Das gilt beispielsweise dann, wenn das Zufallsexperiment aus zwei (oder mehr) unabhängig voneinander durchgeführten
Teil-Zufallsexperimenten besteht. Betrachten wir dazu ein
Beispiel: Das obige Beispiel 2 (es wird ein roter und ein blauer Würfel geworfen)
besteht aus zwei derartigen Teil-Zufallsexperimenten (roter Würfel und blauer Würfel).
Das Ereignis
C = "Die Augenzahl des roten Würfels ist kleiner als 3 und
jene des blauen ist gerade"
lässt sich zusammensetzen aus den Ereignissen
A = "Die Augenzahl des roten Würfels ist kleiner als 3".
B = "Die Augenzahl des blauen Würfels ist gerade".
|
|
|
C
heißt Verbundereignis, da es ein "Verbund" aus zwei Ereignissen
A und B
der Teil-Zufallsexperimente ist.
Es lässt sich in der
Form C = A Ç B
schreiben, wobei
A und B
statistisch voneinander unabhängig sind.
Für die Wahrscheinlichkeiten von Ereignissen dieser Art gibt es nun eine einfache Berechnungsformel, die so genannte
Multiplikationsregel für unabhängige Ereignisse.
Sie gilt generell für Ereignisse A und B,
die statistisch voneinander unabhängig sind (daher insbesondere auch, wenn sie ein Verbundereignis definieren) und
lautet:
| | | |

Durchschnittsmenge

logisches "und"
| |
| | |
|
p(A und B) º
p(A Ç B) º
p(A Ù B) = p(A) p(B).
|
|
|
(9) |
In Worten: Sind A und B
statistisch voneinander unabhängig, so ist die Wahrscheinlichkeit, dass
A und B eintreten,
gleich dem Produkt der Wahrscheinlichkeiten von A und
B.
Beispiel: Auf einer Party sind 15 Frauen und 15 Männer. Unter ihnen werden 3 Tombolapreise
verlost (so dass jede Person nur einen Preis bekommen kann, und selbstverständlich ist die
Aussicht auf einen Gewinn vom Geschlecht unabhängig).
Wir groß ist die Wahrscheinlichkeit, dass eine zufällig ausgewählte Person
eine Frau ist, die einen Preis gewonnen hat?
Lösung:
- Die Ereignisse "die ausgewählte Person ist weiblich" und "die ausgewählte Person hat einen Preis gewonnen"
sind laut Voraussetzung statistisch voneinander unabhängig.
- Die Wahrscheinlichkeit, dass die ausgewählte Person weiblich ist, ist nach (4) der Quotient Zahl der Frauen / Gesamtzahl der Personen
= 15/30 = 1/2.
- Die Wahrscheinlichkeit, dass die ausgewählte Person einen Preis gewonnen hat, ist nach (4) der Quotient Zahl der Preise / Gesamtzahl der Personen
= 3/30 = 1/10.
- Daher ist die gesuchte Wahrscheinlichkeit nach (9) gleich dem Produkt (1/2) × (1/10) = 1/20.
Wir werden weiter unten genauer auf den Begriff der statistischen Unabhängigkeit eingehen und
(9) ganz allgemein beweisen.
An dieser Stelle erwähnen wir nur, dass sich auch die Umkehrung erweisen wird: Zwei Ereignisse, die
(9) erfüllen, sind statistisch voneinander unabhängig, auch wenn
sie kein Verbundereignis definieren.
Vorläufig wollen wir uns vor allem merken, dass (9) dazu benutzt werden kann, um
Wahrscheinlichkeiten von Durchschnittsereignissen zu berechnen, wenn die
statistische Unabhängigkeit von A und B
(wie im soeben durchgerechneten Beispiel) von vornherein klar ist.
|
| | |
für Verbundereignisse
| |
| | |
| | | |
Zum Seitenanfang | |
| | |
Zufallsexperimente bestehen oft aus mehreren Schritten, die hintereinander ausgeführt
werden, wobei jeder Schritt ein eigenes Zufallsexperiment ist, dessen
Details vom Ausgang des vorigen Schritts abhängen können.
Obwohl für gewisse Typen von Zufallsexperimenten rechnerische Abzählmethoden
zur Verfügung stehen (wir werden sie im nächsten Abschnitt besprechen),
kann die Ermittlung von Wahrscheinlichkeiten in solchen Fällen recht schnell unübersichtlich werden.
Es gibt aber eine relativ einfache grafische Darstellungsform, die immer dann
angewandt werden kann, wenn die Zahl der möglichen (bzw. interessierenden) Versuchsausgänge
der Zwischenschritte nicht zu groß ist: die Baumdiagramme. Wir demonstrieren ihr
Prinzip anhand zweier Beispiele.
In einem Baumdiagram werden die Ausgänge eines Zufallsexperiments als Linien
dargestellt und die entsprechenden Wahrscheinlichkeiten dazugeschrieben.
Erinnern wir uns an die im
obigen Beispiel 3 gegebene Urne mit 10 roten,
15 blauen und 5 grünen Kugeln,
wobei Kugeln gleicher Farbe nicht unterschieden werden und eine Kugel zufällig herausgegriffen wird.
Die Wahrscheinlichkeiten, mit denen Kugeln der drei vorkommenden Farben gezogen werden, haben wir
bereits berechnet:
p(rote Kugel) = 1/3
p(blaue Kugel) = 1/2
p(grüne Kugel) = 1/6
Die Summe dieser Wahrscheinlichkeiten ist 1. (Wir wissen wegen (8), dass das so sein muss).
Dieses Zufallsexperiment wird durch folgendes Diagramm dargestellt:
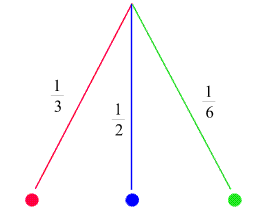
Jeder Versuchsausgang wird als Linie eingezeichnet. Die entsprechenden Wahrscheinlichkeiten sind dazugeschrieben.
Die Kugelsymbole am Ende jeder Linie und die Farben der Linien kennzeichnen die einzelnen
Versuchsausgänge. (Die Kugelsymbole können natürlich durch entsprechende Beschriftungen ersetzt werden).
Die Linien entsprechen disjunkten (einander ausschließenden) Ereignissen.
Das Diagramm ist vollständig in dem Sinn, dass alle möglichen Versuchsausgänge
eingezeichnet sind und deren Wahrscheinlichkeiten sich zu 1 addieren.
Schon an diesem einfachen Diagramm können Wahrscheinlichkeiten abgelesen werden:
- p(rote Kugel)
wird aus der Beschriftung der Linie, die im roten Kugelsymbol endet, als
1/3 abgelesen.
- p(rote oder blaue Kugel)
wird bestimmt, indem die Wahrscheinlichkeiten der roten und der blauen Linie addiert werden
und ergibt sich zu 1/3 + 1/2 = 5/6.
Was dahinter steht, ist einfach die Additionsregel (5) für disjunkte Ereignisse.
- Als Check ermitteln wir noch die Gesamtwahrscheinlichkeit:
p(rote oder blaue oder grüne Kugel)
wird bestimmt, indem die Wahrscheinlichkeiten der roten, der blauen und der grünen Linie addiert werden
und ergibt sich zu 1/3 + 1/2 +1/6 = 1.
Was dahinter steht, ist einfach die Additionsregel (6) für mehr als zwei disjunkte Ereignisse.
Das Ergebnis ist natürlich genau (8), die Normierung der Wahrscheinlichkeiten.
Die Regeln zum Ablesen der Wahrscheinlichkeit eines Ereignisses A aus dem obigen Baumdiagramm lauten:
- Man bestimme jene Linien, die zu A gehören und
- addiere die entsprechenden Wahrscheinlichkeiten.
Nun wollen wir ein komplizierteres Zufallsexperiment betrachten. Wir nehmen dieselbe Urne und ziehen
hintereinander zwei Kugeln, ohne die erste zurückzulegen. Es kann dann beispielsweise gefragt werden, mit welcher
Wahrscheinlichkeit eine rote und eine blaue Kugel (egal in welcher Reihenfolge) gezogen werden.
Dadurch wird alles schlagartig komplizierter. Die Wahrscheinlichkeiten für die erste Ziehung
sind zwar dem obigen Baumdiagramm zu entnehmen, aber danach fehlt eine Kugel, und die Wahrscheinlichkeiten
für die zweite Ziehung hängen davon ab, welche Farbe die zuerst gezogene Kugel hat.
Das Prinzip des Baumdiagramms besteht nun darin, an das Ende jeder Linie, die einem Ausgang der ersten Ziehung
entspricht, eine weitere Verzweigung anzuhängen, die die zweite Ziehung (unter den
entsprechenden neuen Umständen) darstellt. Das Diagramm, das wir auf diese Weise erhalten,
sieht so aus:
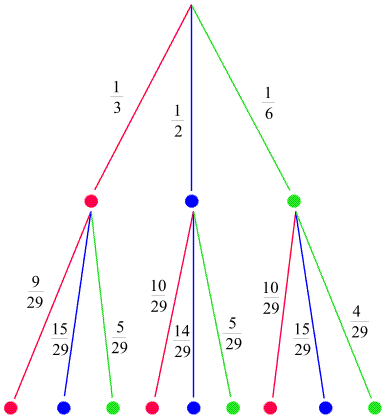
Für die Möglichkeiten der zweiten Ziehung wurden ebenfalls Wahrscheinlichkeiten
eingetragen. Dabei handelt es sich um die für jede Ziehung separat ermittelten
Wahrscheinlichkeiten. (Die Berechnung funktioniert genauso wie im Fall der ersten Ziehung,
mit Hilfe der Formel (4), nur mit den entsprechend veränderten Zahlen der noch in der Urne verbliebenen Kugeln.
Dass die Zahl 29 im Nenner dieser Wahrscheinlichkeiten steht, kommt natürlich daher, dass
sich nach der ersten Ziehung nur mehr 29 Kugeln in der Urne befinden).
Die Wahrscheinlichkeiten für jedes (einer Ziehung entsprechenden) Unterdiagramm summieren sich
zu 1 auf.
(Führen Sie zur Übung diese Rechnungen selbst durch!)
Die neuen Endpunkte der Linien der zweiten Generation werden mit den Symbolen für die Kugeln, die in der zweiten Ziehung auftreten, gekennzeichnet.
(Sie können natürlich auch entsprechend beschriftet werden).
Jeder konkrete Ablauf des gesamten Experiments entspricht einem Pfad vom obersten Verzweigungspunkt des Diagramms
bis zu einem Endpunkt ganz unten.
Wir bezeichnen nun das Ereignis
"Es wird eine rote und eine blaue Kugel gezogen (egal in welcher Reihenfolge)"
mit A und
fragen nach seiner Wahrscheinlichkeit.
Dazu beobachten wir, dass es für das Eintreten von A zwei Möglichkeiten gibt:
Entweder wird zuerst eine rote und dann eine blaue Kugel gezogen
oder umgekehrt. Jede dieser Möglichkeiten entspricht einem Pfad, der aus zwei hintereinander geschalteten Linien besteht, für die jeweils eine
Wahrscheinlichkeit angegeben ist.
Es lässt sich nun im Sinne von (3)
mit relativen Häufigkeiten argumentieren, dass die Wahrscheinlichkeit für das Eintreten eines solchen Pfades
das Produkt der entlang ihm verzeichneten Wahrscheinlichkeiten ist.
(Wir nennen das die Multiplikationsregel für Baumdiagramme).
Für die beiden Pfade unseres Beispiels berechnen wir also:
| | | |
| |
| | |
- p(erst rot, dann blau) = (1/3) × (15/29) = 5/29.
- p(erst blau, dann rot) = (1/2) × (10/29) = 5/29.
(Die Wahrscheinlichkeiten sind gleich! Können Sie argumentieren, warum?)
Diese Pfad-Wahrscheinlichkeiten werden nun (wegen (5), da Pfade disjunkte Ereignisse darstellen)
addiert. Das Ergebnis ist:
p(A) = 5/29 + 5/29 = 10/29.
Soll aus dem Diagramm die Wahrscheinlichkeit, dass die erste gezogene Kugel blau oder grün ist,
ermittelt werden, so sind dafür nur die entsprechenden Linien der ersten Ziehung heranzuziehen: Wir addieren die ihnen zugeordneten
Wahrscheinlichkeiten und erhalten 1/2 + 1/6 = 2/3.
In diesem Fall bestehen die relevanten Pfade jeweils nur aus einer einzigen Linie.
(Hätten wir auch alle nachfolgenden Linien bis zum unteren Ende des Diagramms berücksichtigt, so hätten wir
aufgrund der Normierung der Wahrscheinlichkeiten in den nachfolgenden Teildiagrammen nach einer
etwas längeren Rechnung dasselbe Resultat erhalten).
Damit haben wir die allgemeinen Regeln zur Ermittlung der Wahrscheinlichkeit eines Ereignisses A
in einem Baumdiagramm illustriert. Sie lauten:
- Man bestimme jene Pfade, die zu A gehören
(wobei jeder Pfad beim obersten Verzweigungspunkt beginnt),
- multipliziere die Wahrscheinlichkeiten entlang dieser Pfade und
- addiere die erhaltenen Zahlen.
Auf diese Weise lassen sich aus unserem Diagramm die Wahrscheinlichkeiten für beliebige
Ereignisse ermitteln. Die Berechnung der Wahrscheinlichkeit, dass die zweite gezogene Kugel
grün ist, sieht beispielsweise so aus:
p(Die zweite gezogene Kugel ist grün) =
(1/3) × (5/29) + (1/2) × (5/29) + (1/6) × (4/29) = 5/87 + 5/58 + 2/87 = 1/6.
|
|
|
Versuchen Sie zur Übung, diese Rechnung (und die ihr zugrunde liegenden drei Pfade) nachzuvollziehen!
Berechnen Sie in analoger Weise die Wahrscheinlichkeit, dass die erste gezogene Kugel rot
oder blau, die zweite gezogene Kugel grün ist!
Manche der hier erhaltenen Ergebnisse hätte man auch mit anderen Argumenten (und ein bisschen mehr Theorie)
erhalten können. Demgegenüber stellen Baumdiagramme eine Methode der
"Buchführung" über die Verzweigungen eines sich in mehreren Schritten vollziehenden
Zufallsexperiments dar, bei der nicht allzuviel nachgedacht werden muss, sobald die
Struktur einmal feststeht.
Sie hilft, die Übersicht über die Kombinationen von Einzelschritten zu behalten und
funktioniert natürlich auch für Zufallsexperimente, die sich über mehr als zwei Schritte
erstrecken. Ist die Zahl der einzuzeichnenden Linien nicht zu groß, können Sie dieses
Verfahren immer anwenden.
Zwei Tipps noch zum Abschluss dieses Abschnitts: Manchmal beinhaltet eine Aufgabenstellung Informationen, die in einem
Baumdiagramm nicht benötigt werden. Enthält etwa eine Urne Kugeln zehn verschiedener
Farben und soll eine Wahrscheinlichkeit berechnet werden, bei der lediglich rote und blaue Kugeln
eine Rolle spielen, so können Sie den Typ "andere Kugel" einführen
und so die Zahl der Linien im Diagram klein halten.
Weiters ist es nicht immer nötig, alle Unterdiagramme zu zeichnen. Sollen im obigen
Beispiel etwa nur Ereignisse betrachtet werden, bei der die erste Ziehung keine grüne Kugel
ergibt, so können Sie sich das Zeichnen des dritten Teildiagramms der zweiten Generation
sparen. Das auf diese Weise erhaltene "unvollständige Baumdiagramm"
stellt dann ein Zufallsexperiment dar, bei dem, sollte zuerst eine grüne Kugel
gezogen werden, keine zweite Ziehung mehr stattfindet (siehe den Button rechts).
|
| | |
unvollständiges
diagramm
| |
| | |
| | | |
Zum Seitenanfang | |
| | |
Wir haben im vorigen Abschnitt mit den Baumdiagrammen eine Methode kennen gelernt,
die es erlaubt, Wahrscheinlichkeiten von Ereignissen zu berechnen, die sich auf
Auswahl- und ähnliche Vorgänge beziehen. Manchmal helfen aber auch
Baumdiagramme nicht weiter, insbesondere, wenn es zu viele Möglichkeiten gibt, um sie zeichnen zu können.
Die gute Nachricht besteht aber darin, dass viele Zufallsexperimente auf Laplace-Experimente
(deren Versuchsausgänge alle gleich wahrscheinlich sind) zurückgeführt werden können
und sich die Berechnung von Wahrscheinlichkeiten mit (4) auf das
Abzählen von Möglichkeiten reduziert. Die Kombinatorik
ist die Lehre von den Abzählverfahren und liefert einige nützliche
Formeln, die in der Wahrscheinlichkeitsrechnung angewandt werden können.
Wir wollen ein paar Fälle besprechen und Beispiele angeben, die vorgestellten Formeln aber
nicht beweisen.
Sie werden in Ihrer Mathematik-Ausbildung manche der nachfolgenden Formeln benötigen, manche vielleicht nicht.
Je nach ihrem Lernstoff können Sie diesen Abschnitt beim ersten Lesen
überspringen oder sich auf die von Ihnen benötigten
Themen beschränken. Greifen Sie einfach bei Bedarf auf ihn zurück!
Permutationen
| | | |
| |
| | |
Eine Permutation von n Elementen
(im zweiten Funktionen-Kapitel als bijektive Funktion
beschrieben) ist eine
Verteilung der n Elemente auf
n Plätze.
Es gibt
verschiedene Permutationen von n Elementen.
Aufgabe: Auf wie viele Arten können sich 5 Personen auf 5 freie (unterscheidbare) Plätze verteilen?
Lösung: Auf 5! = 120 Arten.
Aufgabe: Jemand hat sich eine genaue Sitzordnung für die Personen der vorigen Aufgabe ausgedacht, kommt aber
zu spät - die Gäste haben sich bereits (zufällig) auf die vorhandenen 5 Plätze verteilt.
Wie groß ist die Wahrscheinlichkeit, dass sich jede Person auf den ihr zugedachten Platz gesetzt hat?
Lösung: Mit (4) beträgt sie 1/5! = 1/120.
(Die "Zahl der möglichen Fälle" ist 120, die
"Zahl der günstigen Fälle" ist 1).
Kombinationen ohne Wiederholung
| | | |
Permutationen

Faktorielle
| |
| | |
Bei den nächsten vier Formeln geht es um Auswahlverfahren. Der besseren Vorstellung halber stellen
wir uns vor, einzelnen Elementen eine "Schleife" umzubinden und sie dadurch auszuwählen.
In jedem der nun zu besprechenden Fälle kommt es darauf an, ob die Schleifen unterscheidbar sind und ob
ein Element mehr als eine Schleife bekommen kann.
n (unterscheidbaren) Elementen
sollen k Schleifen umgebunden werden.
Dabei sind die Schleifen nicht unterscheidbar,
und jedes Element darf höchstens eine Schleife bekommen.
Es gibt
(unterscheidbare) Möglichkeiten, das zu tun.
| | | |

Binomialkoeffizienten
| |
| | |
Aufgabe: Auf wie viele Arten kann aus einer Gruppe von 20 Menschen
ein 3-köpfiges Vertretungsteam (dessen Mitglieder alle die
gleichen Kompetenzen haben) gebildet werden?
Lösung: Setzen Sie n = 20
und k = 3.
Das Ergebnis ist 1140.
Aufgabe: Wie oft erklingen die Gläser, wenn 10
Personen einander zuprosten?
Lösung: Setzen Sie n = 10
und k = 2. (Die zwei Schleifen bekommen die Personen, die einander zuprosten).
Das Ergebnis ist 45.
Kombinationen mit Wiederholung
| | | |
| |
| | |
n (unterscheidbaren) Elementen
sollen k Schleifen umgebunden werden.
Dabei sind die Schleifen nicht unterscheidbar,
und jedes Element darf mehrere Schleife bekommen.
Es gibt
(unterscheidbare) Möglichkeiten, das zu tun.
Aufgabe: 50 Sportlerinnen nehmen an 7 Bewerben
teil (bei denen es jeweils genau eine Siegerin gibt). Auf wie viele Arten können die Preise verteilt werden?
Lösung: Setzen Sie n = 50
und k = 7.
Das Ergebnis ist 231917400.
Variationen ohne Wiederholung
| | | |
| |
| | |
n (unterscheidbaren) Elementen
sollen k Schleifen umgebunden werden.
Dabei sind die Schleifen unterscheidbar (z.B. nummeriert),
und jedes Element darf höchstens eine Schleife bekommen.
Es gibt
(unterscheidbare) Möglichkeiten, das zu tun.
Aufgabe: Auf wie viele Arten kann aus einem 20-köpfigen Verein
ein 3-köpfiger Vorstand, bestehend aus VorsitzendeR,
SchriftführerIn und KassierIn, gebildet werden?
Lösung: Setzen Sie n = 20
und k = 3.
Das Ergebnis ist 6840.
Aufgabe: 100 Sportler nehmen an einem Bewerb teil. Einer gewinnt Gold,
einer Silber, einer Bronze. Wie viele mögliche Ausgänge gibt es?
Lösung: Setzen Sie n = 100
und k = 3.
Das Ergebnis ist 970200.
Variationen mit Wiederholung
| | | |
| |
| | |
n (unterscheidbaren) Elementen
sollen k Schleifen umgebunden werden.
Dabei sind die Schleifen unterscheidbar (z.B. nummeriert),
und jedes Element darf mehrere Schleife bekommen.
Es gibt
(unterscheidbare) Möglichkeiten, das zu tun.
Aufgabe: Wie viele "Wörter" können zustande kommen, wenn 5 Buchstaben
(nacheinander) aus einem Alphabet vom Umfang 26
gewählt werden?
Lösung: Setzen Sie n = 26
und k = 5.
Das Ergebnis ist 11881376.
Permutationen mit Gruppen nicht unterscheidbarer Elemente
| | | |
Das
Problem
| |
| | |
n Elemente werden in m Gruppen
vom Umfang n1,
n2,...
nm zusammengefasst
(n1 + n2 + ... + nm = n).
Elemente innerhalb einer Gruppe sind nicht unterscheidbar, Elemente aus verschiedenen
Gruppen sind unterscheidbar. Diesen n Elementen sollen
n Schleifen umgebunden werden.
Dabei sind die Schleifen unterscheidbar (z.B. nummeriert), und jedes Element darf
höchstens eine Schleife bekommen. Anders ausgedrückt: Die
n Elemente sollen auf
n Plätze angeordnet
(oder in eine Reihenfolge gebracht) werden.
Es gibt
(unterscheidbare) Möglichkeiten, das zu tun.
Aufgabe: Auf wie viele (unterscheidbare) Arten können 10 weiße, 12 schwarze
und 14 rote Kugeln auf 36 Plätze
angeordnet werden? (Dabei wird angenommen, dass Kugeln einer Farbe nicht unterschieden werden können).
Lösung: Setzen Sie n = 36
(die Zahl der Plätze und gleichzeitig die Zahl der Kugeln),
m = 3,
n1 = 10,
n2 = 12,
n3 = 14.
(Die Schleifen, die die Kugeln bekommen, bedeuten etwa die Nummer der Plätze, auf die sie zu liegen kommen).
Das Ergebnis ist 2454860399191200.
Mit diesen Formeln ausgerüstet, versuchen Sie beim Bearbeiten konkreter Aufgabenstellungen,
in denen derartige Auswahl- und Anordnungsprozeduren vorkommen,
zuerst herauszufinden, um welchen Typ es sich handelt,
was die "Elemente" und was die "Schleifen" sind.
Das ist nicht immer leicht, und für manche Probleme gibt es (je nachdem, wie man
sie betrachtet) zwei Formeln, die für sie zuständig sind (und natürlich das gleiche Resultat ergeben).
Aber wenn Sie es geschafft haben, haben Sie schon gewonnen, denn der Rest besteht nur im Einsetzen von Zahlen
in die entsprechende Formel.
Um Rechnungen durchzuführen, die Faktorielle und
Binomialkoeffizienten enthalten (und bei denen manchmal sehr große Zahlen auftreten)
können Sie unser Tool
Online-Rechnen mit Mathematica
benutzen. Geben Sie dazu
beispielsweise 10! oder
Binomial[20,2] ein!
|
| | |
| |
| | |
| Bedingte Wahrscheinlichkeit |
| | | |
Zum Seitenanfang | |
| | |
In zahlreichen Anwendungsfällen tritt das Problem auf, dass nur solche Versuchsausgänge
eines Zufallsexperiments von Interesse sind, bei denen ein bestimmtes Ereignis
B eintritt.
Damit tritt eine neue Fragestellung auf:
Wie groß ist die Wahrscheinlichkeit für das Eintreten eines
Ereignisses A unter der Voraussetzung, dass
B eingetreten ist?
Multiplikationsregel für Wahrscheinlichkeiten
| | | |
| |
| | |
Um sie zu beantworten, betrachten wir jene Teilmenge E ' des Ereignisraums E,
das nur aus jenen "interessanten" Versuchsausgängen besteht, die im
Ereignis B enthalten sind.
Genau genommen wird dadurch ein neues Zufallsexperiment mit
Ereignisraum E ' des Ereignisraums E,
das nur aus jenen "interessanten" Versuchsausgängen besteht, die im
Ereignis B enthalten sind.
Genau genommen wird dadurch ein neues Zufallsexperiment mit
Ereignisraum E '
definiert.
(In der Praxis besteht es darin, dass alle Versuchsausgänge, bei denen
B nicht eintritt, ignoriert werden).
Die bedingte Wahrscheinlichkeit des Ereignisses A
"unter der Voraussetzung B"
ist nun nach (3) definiert als
die vorausgesagte relative Häufigkeit des Auftretens von A
in einer gegen unendlich strebenden Anzahl von Durchführungen des neuen
Zufallsexperiments. Sie wird in der Form
p(A|B)
angeschrieben und ausgesprochen als "bedingte Wahrscheinlichkeit von A unter
der Voraussetzunng B". '
definiert.
(In der Praxis besteht es darin, dass alle Versuchsausgänge, bei denen
B nicht eintritt, ignoriert werden).
Die bedingte Wahrscheinlichkeit des Ereignisses A
"unter der Voraussetzung B"
ist nun nach (3) definiert als
die vorausgesagte relative Häufigkeit des Auftretens von A
in einer gegen unendlich strebenden Anzahl von Durchführungen des neuen
Zufallsexperiments. Sie wird in der Form
p(A|B)
angeschrieben und ausgesprochen als "bedingte Wahrscheinlichkeit von A unter
der Voraussetzunng B".
Ihre Berechnung kann auf jene Versuchsausgänge, bei denen
A und B
eintreten, zurückgeführt werden. Wie oben ausgeführt, entspricht das
dem Durchschnitt
A Ç B.
Für diesen gilt nun die allgemeine
Multiplikationsregel für Wahrscheinlichkeiten
| | | |
| |
| | |
|
p(A und B) º
p(A Ç B) = p(A|B) p(B).
|
|
|
(16) |
Ist p(B) ¹ 0,
so kann mit ihrer Hilfe p(A|B)
berechnet werden und ist damit auf Größen zurückgeführt, die sich
als "gewöhnliche" Wahrscheinlichkeiten
im Rahmen des gegebenen Zufallsexperiments ausdrücken lassen.
(Ist p(B) = 0,
so ist die bedingte Wahrscheinlichkeit p(A|B) nicht definiert).
Statistische Unabhängigkeit
| | | |
| |
| | |
Der Begriff der bedingten Wahscheinlichkeit erlaubt uns, zu entscheiden,
ob zwei Ereignisse statistisch voneinander abhängen.
Betrachten wir einen Zufallsprozess und zwei Ereignisse
A und B.
Wir nennen A
statistisch (oder stochastisch) von B
unabhängig, wenn
ist. In Worten ausgedrückt, besagt diese Beziehung: Die Wahrscheinlichkeit für das Eintreten von A
ist unabhängig davon, ob
alle Versuchsausgänge berücksichtigt werden
oder nur jene, bei denen B eintritt.
Bemerkung: Unter anderem gilt (17) für die oben im Zusammenhang mit (9) betrachteten
Ereignisse von Teil-Zufallsexperimenten, durch die Verbundereignisse ausgedrückt werden.
Setzen wir nun voraus, dass A
statistisch von B
unabhängig ist. Durch Einsetzen von (17) in (16)
erhalten wir sofort die Multiplikationsregel für unabhängige Ereignisse (9).
Gilt umgekehrt (9), so erhalten wir, da p(B) ¹ 0
vorausgesetzt ist, durch Vergleich mit (16) genau (17) zurück.
Bemerkungen:
- Aufgrund der Symmetrie dieses Resultats ist A genau dann
statistisch von B
unabhängig ist, wenn B
statistisch von A
unabhängig ist. Wir nennen die beiden Ereignisse einfach statistisch voneinander unabhängig.
- Wir haben gezeigt, dass A und B
genau dann statistisch voneinander unabhängig sind, wenn (9) gilt.
Damit ist die allgemeine Anwendbarkeit von (9) für statistisch voneinander unabhängige Ereignisse bewiesen.
Der Begriff der bedingten Wahrscheinlichkeit erschließt eine neue Art von Fragestellung,
der wir uns nun zum Abschluss zuwenden.
|
| | |
| |
| | |
| | | |
Zum Seitenanfang | |
| | |
Wir werden nun eine Problematik besprechen, die in praktischen Anwendungen relevant ist.
Die angesprochene Thematik ist komplexer als die bisherigen Teile dieses Kapitels
und daher etwas schwieriger zu lesen.
Je nach ihrem Lernstoff können Sie diesen letzten Abschnitt auslassen
(obwohl wir ihn Ihnen sehr ans Herz legen).
Über viele Phänomene
(vom Wetter über den zukünftigen Gesundheitszustand eines Menschen bis
zum Verhalten einzelner Atome) lassen sich nur unsichere Aussagen treffen.
Wir greifen dann auf die Wahrscheinlichkeitsrechnung zurück, um
die von der mathematischen Theorie definierten und analysierten Zufallsexperimente als Modelle
für reale Vorgänge heranzuziehen.
So interessiert uns etwa, wie die Ausbildung medizinischer Symptome oder
das Auftreten von Erdbeben durch "zufallsgesteuerte" Prozesse
modelliert werden können. Dabei besteht aber ein prinzipielles Problem:
Unseren Beobachtungen und Messungen zugänglich sind lediglich
die "Versuchsausgänge" und ihre (bisher aufgetretenen) Häufigkeiten,
nicht aber die Wahrscheinlichkeiten "an sich".
Die ideale Forderung, ein Zufallsexperiment (in identischer Weise) beliebig oft, ja "unendlich oft"
durchzuführen, vgl. (3), ist in der Praxis nicht erfüllbar.
Daher sind wir oft auf Wahrscheinlichkeitsmodelle angewiesen, deren
Eigenschaften wir nur ungenau kennen.
Ein typischer Fall von Unsicherheit dieser Art besteht,
wenn zwei konkurrierende Modelle gewisse Beobachtungsdaten erklären können
und wir wissen möchten, welchem Modell wir den Vorzug geben sollen. Im Folgenden
werden wir diese Art von Fragestellung anhand eines einfachen Beispiels
diskutieren.
Der Begriff der bedingten Wahrscheinlichkeit wird dabei eine wichtige Rolle spielen.
Als "Modelle" dienen zwei Würfel, ein fairer und ein
unfairer, und die Beobachtungsdaten werden durch eine einmal gewürfelte Augenzahl
dargestellt.
Der Satz von Bayes anhand eines Beispiels
| | | |
| |
| | |
Stellen wir uns vor, jemand besitzt zwei Würfel:
- einen fairen, dessen Augenzahlen alle mit Wahrscheinlichkeit 1/6 auftreten,
- und einen unfairen, dessen Verhalten durch die Tabelle
| Augenzahl | Wahrscheinlichkeit |
| 1 | 1/5 |
| 2 | 1/5 |
| 3 | 1/5 |
| 4 | 1/5 |
| 5 | 1/6 |
| 6 | 1/30 |
charakterisiert wird. (Die Summe der Wahrscheinlichkeiten ist 1).
Er wählt einen der beiden Würfel aus und wirft ihn. Der Ausgang ist "Augenzahl 6".
Mehr erfahren wir nicht.
Was uns nun besonders interessiert, ist, welchen der beiden Würfel er
benutzt hat - den fairen oder den unfairen?
Es geht in dieser Frage nicht darum, die Wahrscheinlichkeit eines Versuchsausgangs
für ein gegebenes Zufallsexperiment anzugeben, sondern von einem
Versuchsausgang auf die Natur des Zufallsexperiments rückzuschließen.
Anmerkung:
Diese Logik passt wunderbar auf Anwendungssituationen, da Ausgänge von Zufallsexperimenten
unseren Beobachtungen und Messresultaten entsprechen.
Denken Sie etwa bei den zwei Würfeln an Krankheiten, die mit verschiedenen Wahrscheinlichkeiten
zum gleichen Symptom führen, bei "Augenzahl 6" an das Symptom und bei der
Frage, welcher Würfel verwendet wurde, an einen Menschen, der wissen möchte,
auf welche der beiden Krankheiten sein Symptom zurückgeht!
Natürlich wissen wir nicht mit Sicherheit, welcher Würfel benutzt wurde, denn "Augenzahl 6" ist mit beiden Würfeln
möglich. Können wir aber eine begründete Wahrscheinlichkeitsaussage
darüber machen? Wir könnten die bedingten Wahrscheinlichkeiten
p(6 | | F) = 1/6
und
p(6 F) = 1/6
und
p(6 | | U) = 1/30,
d.h. die Wahrscheinlichkeiten für "Augenzahl 6" unter der Voraussetzung, dass der faire bzw. der
unfaire Würfel verwendet wurde, heranziehen (was man intuitiv vielleicht zunächst tun würde). Nur leider lösen diese unser
Problem nicht, denn wir fragen nach dem verwendeten Würfel und nicht nach der
gewürfelten Augenzahl. U) = 1/30,
d.h. die Wahrscheinlichkeiten für "Augenzahl 6" unter der Voraussetzung, dass der faire bzw. der
unfaire Würfel verwendet wurde, heranziehen (was man intuitiv vielleicht zunächst tun würde). Nur leider lösen diese unser
Problem nicht, denn wir fragen nach dem verwendeten Würfel und nicht nach der
gewürfelten Augenzahl.
Interessanterweise können wir mit dem uns zur Verfügung stehenden Wissen
nicht einmal eine Wahrscheinlichkeitsaussage treffen, denn es fehlt uns noch ein Stück Information: die Wahrscheinlichkeiten,
aufgrund derer der Würfelbesitzer einen der beiden Würfel ausgewählt hat.
Wir nennen sie die Apriori-Wahrscheinlichkeiten. Ganz allgemein werden
mit diesem Begriff Wahrscheinlichkeiten bezeichnet,
aufgrund derer eines von mehreren Zufallsexperimenten ausgewählt wird.
Bezeichnen wir die Apriori-Wahrscheinlichkeiten für die beiden Würfel mit
- pa(F) für die Wahl des fairen Würfels und
- pa(U) für die Wahl des unfairen Würfels.
Nun können wir den gesamten Ablauf (Wahl eines Würfels und Werfen dieses Würfels) zu einem einzigen
Zufallsexperiment erklären. Stellen wir es durch ein Baumdiagramm dar:
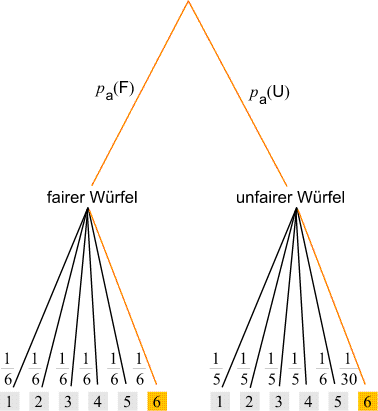
Zuerst wird - entsprechend der Aproiri-Wahrscheinlichkeiten -
einer der beiden Würfeln gewält und danach wird gewürfelt.
(Die Wahrscheinlichkeiten für die Augenzahlen der Würfel stehen immer links von der entsprechenden Linie).
Die Augenzahl 6 kann von beiden Würfeln kommen - diese zwei Möglichkeiten
werden durch die beiden hervorgehobenen Pfade dargestellt.
Diesen beiden Pfaden können wir nun (nach den oben besprochenen) allgemeinen Regeln
ihre Wahrscheinlichkeiten zuordnen:
- Der Pfad, der vom fairen Würfel zur Augenzahl 6 führt, besitzt die Wahrscheinlichkeit
p(F und 6) = pa(F)/6.
- Der Pfad, der vom unfairen Würfel zur Augenzahl 6 führt, besitzt die Wahrscheinlichkeit
p(U und 6) = pa(U)/30.
Nun kehren wir zu unserer eigentlichen Fragestellung zurück. Entschließen wir uns, all jene
Versuchsausgänge zu ignorieren, bei denen nicht die Augenzahl 6 gewürfelt wird, so
führt dies genau auf die oben besprochenen bedingten Wahrscheinlichkeiten.
Aus Formel (16) folgt dann
p(F und 6) = p(F | | 6) p(6) 6) p(6)
p(U und 6) = p(U | | 6) p(6) 6) p(6)
|
|
(18) |
Die bedingten Wahrscheinlichkeiten
p(F | | 6)
und
p(U 6)
und
p(U | | 6)
beantworten unsere Frage: Sie stellen die Wahrscheinlichkeiten dar, dass der faire bzw. der unfaire Würfel
verwendet wurde unter der Voraussetzung, dass die Augenzahl 6 war
(was genau der uns zugänglichen Information entspricht).
Unter Verwendung der Pfadwahrscheinlichkeiten (Produkt der Wahrscheinlichkeiten
der Linien eines Pfades) ergibt sich 6)
beantworten unsere Frage: Sie stellen die Wahrscheinlichkeiten dar, dass der faire bzw. der unfaire Würfel
verwendet wurde unter der Voraussetzung, dass die Augenzahl 6 war
(was genau der uns zugänglichen Information entspricht).
Unter Verwendung der Pfadwahrscheinlichkeiten (Produkt der Wahrscheinlichkeiten
der Linien eines Pfades) ergibt sich
p(F | | 6) = p(6)-1 pa(F)/6 6) = p(6)-1 pa(F)/6
p(U | | 6) = p(6)-1 pa(U)/30 6) = p(6)-1 pa(U)/30
|
|
(19) |
Die Summe dieser beiden Größen ist gleich 1 (wie es sein muss und wie sich durch Berechnung von
p(6),
der Gesamtwahrscheinlichkeit für das Eintreten von "Augenzahl 6", leicht nachrechnen lässt).
Wir können uns die Berechnung aber sparen und statt dessen die Normierungsbedingung
p(F | | 6)
+ p(U 6)
+ p(U | | 6) = 1
verwenden, um die Konstante p(6)
in (19) zu ermitteln. 6) = 1
verwenden, um die Konstante p(6)
in (19) zu ermitteln.
Sehen wir uns das Ergebnis (19) und seine Konsequenzen nun genauer an:
- Über den verwendeten Würfel können wir
erst dann eine (Wahrscheinlichkeits-)Aussage machen, wenn die Apriori-Wahrscheinlichkeiten
pa(F) und
pa(U)
der Würfelwahl bekannt sind.
- In (19) treten die bedingten Wahrscheinlichkeiten
p(6
 | | F) = 1/6
und
p(6 F) = 1/6
und
p(6 | | U) = 1/30
auf, d.h. die Wahrscheinlichkeiten für "Augenzahl 6" unter der Voraussetzung, dass der faire bzw. der
unfaire Würfel verwendet wurde. Sie sind aber (vielleicht entgegen der ersten intuitiven Erwartung) nutzlos, solange die
Apriori-Wahrscheinlichkeiten nicht bekannt sind. U) = 1/30
auf, d.h. die Wahrscheinlichkeiten für "Augenzahl 6" unter der Voraussetzung, dass der faire bzw. der
unfaire Würfel verwendet wurde. Sie sind aber (vielleicht entgegen der ersten intuitiven Erwartung) nutzlos, solange die
Apriori-Wahrscheinlichkeiten nicht bekannt sind.
- Die Beziehungen (19) können auch in der Form
p(F | | 6) = p(6)-1 pa(F) p(6 6) = p(6)-1 pa(F) p(6 | | F) F)
p(U | | 6) = p(6)-1 pa(U) p(6 6) = p(6)-1 pa(U) p(6 | | U) U)
|
|
(20) |
angeschrieben werden. In ihnen treten die Ereignisse in den bedingten Wahrscheinlichteiten
links und rechts in vertauschten Rollen auf.
- Beachten Sie die allgemeine Struktur von (20): Die Wahrscheinlichkeit, dass ein bestimmter Würfel
verwendet wurde, ist proportional
zum Produkt aus der Apriori-Wahrscheinlichkeit für die Wahl dieses
Würfels und der Wahrscheinlichkeit, dass mit ihm die Augenzahl 6 erzielt wird.
Das Entscheidende an diesen Beziehungen lässt sich in der Form
p(Würfel | | 6) = C pa(Würfel) p(6 6) = C pa(Würfel) p(6 | | Würfel) Würfel)
|
|
(21) |
zusammenfassen, wobei "Würfel" für "F" oder "U" stehen kann
und C eine Konstante ist (die sich aus
der Normierungsbedingung ergibt, dass die Summe dieser Wahrscheinlichkeiten über beide Würfel gleich
1 ist).
- Hinter der Vertauschung der Rollen der Ereignisse in den bedingten Wahrscheinlichkeiten
in (20) steht eine allgemeine Beziehung, die aus der Multiplikationsregel (16) hergeleitet werden kann,
indem deren Symmetrie in
A und B
verwendet wird: Für beliebige Ereignisse eines Zufallsexperiments gilt
|
p(A|B) p(B) = p(B|A) p(A).
|
|
|
(22) |
Diese Formel heißt Satz von Bayes.
Angewandt auf die im Würfelproblem vorkommenden Ereignisse nimmt er die Form (20) oder (21)
an. Manchmal wird auch (16) mit diesem Namen bezeichnet.
- Kehren wir zum Würfelproblem zurück:
Falls jeder der beiden Würfeln mit gleicher Wahrscheinlichkeit gewählt wird, ist
pa(F) =
pa(U) = 1/2.
Damit ergibt sich aus (19
 ), dass sich die Wahrscheinlichkeiten
fairer zu unfairer Würfel wie 30 : 6, also wie 5 : 1
verhalten. Es ist dann
p(F ), dass sich die Wahrscheinlichkeiten
fairer zu unfairer Würfel wie 30 : 6, also wie 5 : 1
verhalten. Es ist dann
p(F | | 6) = 5/6
und
p(U 6) = 5/6
und
p(U | | 6) = 1/6.
In diesem Fall ist es deutlich wahrscheinlicher, dass der faire Würfel verwendet wurde. 6) = 1/6.
In diesem Fall ist es deutlich wahrscheinlicher, dass der faire Würfel verwendet wurde.
- Falls wir mehr Beobachtungsdaten besitzen, können wir den verwendeten Würfel mit größerer Zuverlässigkeit
identifizieren. (Siehe den Button rechts für den Fall, dass eine ganze Sequenz von
Augenzahlen bekannt ist).
Eine Anwendung des Satzes von Bayes
| | | |
von Augenzahlen
| |
| | |
Nachdem wir die Logik des Satzes von Bayes anhand eines einfachen Beispiels ausführlich diskutiert haben,
betrachten wir noch eine Anwendung aus der Medizin.
Aufgabe:
Ein medizinisches Symptom S
kann von zwei bekannten Krankheiten A
und B
hervorgerufen werden (A
ist selten und gefährlich, B
ist häufig und harmlos), aber auch bei gesunden Menschen (C)
auftreten. Wenn das Symptom bei jemandem auftritt, möchte man wissen,
mit welcher Wahrscheinlichkeit er welche Krankheit hat bzw. gesund ist. Epidemiologische
und medizinische Untersuchungen studieren normalerweise nicht direkt
diese Frage, sondern die Häufigkeit von Symptomen bei gegebenen
Krankheiten
| Kategorie |
Auftreten
von S
mit Wahrscheinlichkeit |
| A |
0.5 |
| B |
0.2 |
| C |
0.1 |
und die Erkrankungswahrscheinlichkeiten
| Kategorie |
Erkrankung erfolgt mit
Wahrscheinlichkeit |
| A |
0.01 |
| B |
0.15 |
Wie groß ist unter Zugrundelegung dieser Daten die Wahrscheinlichkeit, dass ein Mensch, der Symptom
S ausbildet, an
A bzw. B
erkrankt bzw. gesund ist?
Lösung:
Die erste Tabelle definiert drei Zufallsexperimente
A
B,
und C.
Die zweite legt fest, mit welchen Apriori-Wahrscheinlichkeiten sie auftreten, wodurch
A,
B,
und C Ereignisse eines
größeren Zufallsexperiments werden.
Das zugehörige Baumdiagramm sieht so aus:
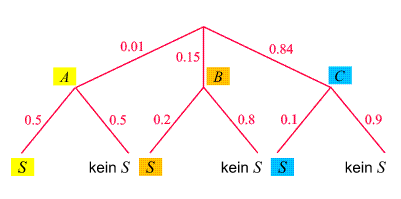
Bei Auftreten des
Symptoms S
sind die Wahrscheinlichkeiten, an A
bzw. B
erkrankt bzw. gesund zu sein, gemäß dem Satz von Bayes (bzw. der entsprechenden Verallgemeinerung von (20) oder (21) auf
drei zur Auswahl stehende Zufallsexperimente) durch
| p(A|S) = |
0.01 × 0.5
|
» 0.042 |
|
|
0.01 × 0.5 + 0.15 × 0.2 + 0.84 × 0.1
|
|
|
| p(B|S) = |
0.15 × 0.2
|
» 0.252 |
|
|
0.01 × 0.5 + 0.15 × 0.2 + 0.84 × 0.1
|
|
|
| p(C|S) = |
0.84 × 0.1
|
» 0.706 |
|
|
0.01 × 0.5 + 0.15 × 0.2 + 0.84 × 0.1
|
|
|
gegeben (wobei die Nenner durch die Normierungsbedingung
p(A|S) + p(B|S) + p(C|S) = 1
zustande kommen). Unser
Patient braucht sich also keine übermäßigen Sorgen zu
machen (obwohl eine Abklärung sinnvoll ist, denn von
1000
Patienten, bei denen das Symptom auftritt, werden ungefähr
40
tatsächlich an A
erkrankt sein).
Bemerkungen:
- Vergleichen Sie den relativ kleinen Wert
p(A|S) » 0.042
mit dem eher großen Wert
p(S|A) = 0.5
aus der ersten Tabelle (der auf einen Menschen mit Symptom S
einen bedrohlichen Eindruck machen mag). Wie ist dieser Unterschied zu erklären? Wie kommt er in der obigen Rechnung zustande?
- Situationen wie die vorliegende werden oft auch anhand von Mengendiagrammen wie diesem
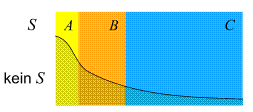
visualisiert. Aus ihm gehen die Kombinationsmöglichkeiten (A, B oder
C, jeweils mit oder ohne S ) hervor.
Bedingte Wahrscheinlichkeiten können hier als Flächeninhalte interpretiert werden,
und der Satz von Bayes ist dann eine Aussage über Beziehungen zwischen diesen Flächeninhalten. ) hervor.
Bedingte Wahrscheinlichkeiten können hier als Flächeninhalte interpretiert werden,
und der Satz von Bayes ist dann eine Aussage über Beziehungen zwischen diesen Flächeninhalten.
- Wenn sich herausstellt, dass der Patient einer für eine Erkrankung an A anfälligen
Risikogruppe angehört, so wirkt sich das auf die für ihn zutreffenden Apriori-Wahrscheinlichkeiten aus.
Das ist eine gute Illustration der Tatsache, dass Wahrscheinlichkeiten unseren Kenntnisstand ausdrücken und sich
mit diesem ändern können.
Der Satz von Bayes eignet sich gut zur Anwendung in derartigen Domänen "unsicheren" Wissens.
Ein weiteres - modernes - Anwendungsgebiet sind Spam-Filter,
d.h. Computerprogramme, die unter den eingehenden E-mails eines Benutzers die Spam-Mails herausfinden sollen.
Neben den Wahrscheinlichkeiten, dass Mails mit gewissen Charakteristika als Spam zu klassifizieren sind, werden die
Apriori-Wahrscheinlichkeiten, dass der Benutzer solche Mails überhaupt bekommt, berücksichtigt.
"Bayessche Spam-Filter" werten beispielsweise Worthäufigkeiten in bereits vom Benutzer erhaltenen und klassifizierten
E-mails aus und sind damit "selbstlernende" Programme, die die verwendeten Apriori-Wahrscheinlichkeiten ständig verbessern.
Damit haben wir unsere Einführung in die Grundsätze der Wahrscheinlichkeitsrechnung beendet.
Wir werden in den nächsten Kapiteln, in denen die Statistik eine größere Rolle spielen wird,
darauf aufbauen.
|
| | |

Wahrsch.rechnung
und Statistik
2 |
3 |
4
| |