|
5.1 Reelle Zahlen
|

 
|
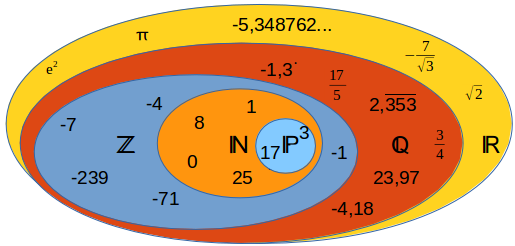
Wenn die rationalen Zahlen dicht sind, also auch zwischen 2 beliebigen, am Zahlenstrahl bereits noch so eng beieinander liegen Zahlen stets weitere Zahlen liegen, dann müsste man doch davon ausgehen können, dass wir nun alle möglichen Zahlen gefunden haben. Oder? Dann müsste man eigentlich auch eine rationale Zahl finden können, die die folgende Gleichung löst:
x2 - 2 = 0
Doch bevor du zu intensiv versuchst einen Bruch, also ein x∈ℤ zu finden, das die obige Gleichung löst, recherchiere lieber zuerst einmal, ob √2 eine rationale Zahl sein kann ...
Es gibt also doch noch Zahlen, die nicht durch Brüche dargestellt werden können. Der (mathematische!) Beweis dafür lässt sich für manche Zahlen vergleichsweise einfach führen. Für andere Zahlen, wie beispielweise π, ist dieser Beweis etwas aufwändiger. Zahlen die nicht als Bruch, also als Verhältnis einer ganzen zu einer natürlichen Zahl dargestellt werden können und damit keine rationalen Zahlen sind, werden als irrationale Zahlen bezeichnet.
|
|
5.3 Welche Menge ist größer: ℚ oder ℝ?
|

  

|
In allen Zahlenmengen die wir bisher kennengelernt haben, gibt es unendlich viele Elemente. Es gibt keine größte natürliche Zahl n ∈ ℕ und damit unendlich viele natürlichen Zahlen. Wir können die alle Elemente der Menge ℕ jedoch abzählen (auch wenn man seeehr lange zählen muss). Die Menge ℕ der natürlichen Zahlen wird daher auch abzählbar unendlich genannt. ℕ ist eine Teilmenge von ℤ, damit müssen in ℤ zumindest gleich viele, also auch unendlich viele Elemente beinhaltet sein.
Auch wenn es auf den ersten Blick seltsam anmutet: ℤ ist nicht "größer" als ℕ! Warum? Weil ich jeder ganzen Zahl eine eindeutige natürliche Zahl zuordnen kann (und umgekehrt). Und so lange das funktioniert, sind zwei Menge gleich mächtig. Betrachte dir z.B. alle natürlichen Zahlen ohne der Null. Mit allen n ∈ ℕ rechnest du nun wie folgt: ist n eine ganze Zahl, so teile sie durch 2. Ist n eine ungerade Zahle so berechne -(n-1)/2. Das ergibt in jedem Fall wieder eine ganze Zahl.
Mache dir in deinem Übungsheft eine Tabelle und berechne dir für die Zahlen von 1 bis 20 die Ergebnisse der obigen Berechnung! Siehst du die eindeutige Abbildung zwischen ℕ und ℤ?
Die ganzen Zahlen sind also ebenfalls abzählbar unendlich. WIe sieht es mit den rationalen Zahlen aus? ℤ ist wiederum eine Teilmenge von ℚ, also wieder mindestens gleich groß. Aber ist ℚ nun wirklich größer als ℕ oder gibt es auch hier eine Möglichkeit alle Elemente von ℚ abzuzählen?
Recherchiere nach einem Beweis oder einer Widerlegung dafür, dass ℚ ebenfalls abzählbar, also gleich mächtig wie ℕ ist. Schreibe dir die Beweisskizze in dein Übungsheft! Ein Tipp: ein Mathematiker namens Georg Cantor hat sich da ein paar sehr gute Gedanken dazu gemacht ...
WIe sieht es nun mit ℝ aus? ℚ ist ja wieder eine Teilmenge von ℝ. Kannst du auch hier eine Möglichkeit finden, alle Elemente von ℝ abzuzählen und damit zu zeigen, dass sie gleich mächtig ist wie ℕ oder nicht?
- Die Menge der natürlichen Zahlen ℕ ist abzählbar unendlich.
- Eine Menge heißt abzählbar, wenn sie endlich groß ist, oder eine eindeutige Abbildung zwischen den natürlichen Zahlen und den elementen dieser Menge besteht.
- Eine Menge heißt überabzählbar, wenn ihre Anzahl der Elemente größer ist, als die der natürlichen Zahlen.
- ℝ ist überabzählbar.
Schreibe dir deine Erkenntnisse oder Verwirrnisse über unendliche Mengen, welche unendlich großen Mengen, die auf den ersten Blick verschieden groß erscheinen, doch gleich groß sind, welche es nicht sind, und woran man das unterscheiden kann, in dein Lernjournal!
Lernstoff, Vertiefung, Eintrag in das Lerntagebuch
|
Lernpfadseite als User öffnen (Login)
Falls Sie noch kein registrierter User sind, können Sie sich einen neuen Zugang anlegen. Als registrierter User können Sie ein persönliches Lerntagebuch zu diesem Lernpfad anlegen.
|



