| | |
| | | |
| |
| | |
| | | |
| |
| | |
Im ersten Kapitel über das Differenzieren haben wir viele nützliche Dinge besprochen,
waren aber in manchen Punkten etwas oberflächlich. Dieses zweite
Kapitel ist nun der Vertiefung der begrifflichen Grundlagen
gewidmet, stellt daher höhere Ansprüche hinsichtlich
Abstraktion und Exaktheit als das erste. Wir beginnen damit, genauer zu definieren,
wann wir eine Funktion als differenzierbar bezeichnen und was die Ableitung ist.
Ableitung
| | | |

Differenzieren 1
| |
| | |
Die Ableitung einer reellen Funktion f an einer gegebenen Stelle
x ist ein "lokales" Konzept, das auf einem Vergleich
des Funktionswerts f(x)
mit Funktionswerten an nahe benachbarten Stellen beruht. Wie "nahe" diese Vergleichsstellen bei
x liegen, ist dabei gleichgültig
- wichtig ist aber, dass es sich um ein Kontinuum von
Vergleichsstellen handelt.
Wir formulieren diese Idee genauer, indem wir verlangen, dass es eine reelle Zahl
a > 0 gibt, so dass
das (offene) Intervall
(x - a, x + a)
ganz im Definitionsbereich von f liegt, d.h.
dass von jedem Element x' dieses
Intervalls der Funktionswert f(x')
wohldefiniert ist. Ein offenes Intervall, in dem x
liegt, bezeichnen wir als Umgebung von x.
Wir verlangen also, dass f in
einer Umgebung von x wohldefiniert ist.
Mit J bezeichnen wir die Menge aller Punkte
des Intervalls (x - a, x + a),
die ungleich x sind.
| | | |
| |
| | |
Definition:
f heißt an der Stelle x
differenzierbar, wenn es eine reelle Zahl c
mit folgender Eigenschaft gibt: Für jede Folge
(x1, x2, ...)
reeller Zahlen
xn Î J,
die gegen x konvergiert, gilt
| |
|
f(xn)
- f(x)
xn -
x |
=
c . |
| lim |
| n ® ¥ |
|
(1) |
Wir nennen dann c die Ableitung von
f an der Stelle x
und bezeichnen sie mit f '(x). |
| | | |

Folgen und
Grenzwerte
| |
| | |
Bemerkungen:
- Besonders wichtig an dieser Definition ist das Wort "jede".
- Der Ausdruck
(f(xn) - f(x))/(xn - x)
ist der Differenzenquotient
bezüglich der Stellen x und
xn.
Geometrisch interpretiert, stellt er den Anstieg der Geraden (Sekante) durch die Punkte
(x, f(x)) und
(xn, f(xn)) dar.
- Falls der Grenzwert (1) für jede der in Frage kommenden Folgen existiert,
schreiben wir symbolisch
| |
|
|
f(x' )
- f(x)
x' -
x |
. |
| f '(x) = |
lim |
| |
x' ® x |
|
(2) |
Intuitiv deutet diese Schreibweise an, dass x'
der Stelle x immer näher kommt.
Genau genommen dürfen wir uns das aber nicht bloß als einen Annäherungsprozess vorstellen
(das entspräche dem Grenzwert (1) für eine Folge). Wichtig ist, dass das Resultat von der Art und Weise,
wie sich x' an x
annähert, nicht abhängen soll.
Die exakte Formulierung dieser Forderung ist die obige Definition.
- Mit e = x' - x
erhalten wir aus (2) die Schreibweise
| |
|
|
f(x
+ e) - f(x)
e |
, |
| f '(x) = |
lim |
| |
e ® 0 |
|
(3) |
die wir im ersten Differenzieren-Kapitel verwendet haben.
- Es gibt eine der Definition (1) gleichwertige Formulierung, die
den Bezug die Begriffe der Folge und der Konvergenz vermeidet.
Sie können sie mit dem nebenstehenden Button aufrufen.
| | | |

Grenzwerte reeller Funktionen

Schreibweise mit e
alternative

| |
| | |
Die meisten "elementaren" mathematischen Funktionen
(insbesondere Polynome, rationale Funktionen, Potenz-, Winkel-, Exponential- und Logarithmusfunktionen)
sind innerhalb ihres Definitionsbereichs differenzierbar
(wobei zunächst über Randstellen nichts gesagt wird, mehr dazu weiter unten).
Mit dem nebenstehenden Button können Sie als Beispiel die genaue Argumentation, die auf die
Differenzierbarkeit und die Ableitung der Funktion
f(x) = x2
führt, aufrufen.
Aufpassen sollten Sie bei abschnittsweise (stückweise) termdefinierten Funktionen und
bei Termen, die die Betragsfunktion enthalten.
Hier ein paar Beispiele von Funktionen, deren die Differenzierbarkeit nicht an allen Stellen
gegeben ist:
Beispiel 1: Die Funktion
| |
{ |
|
x1/3 |
wenn
x ³ 0 |
| f(x) = |
| |
-(-x)1/3 |
wenn
x < 0 |
|
(4) |
ist die Inverse der Funktion
g(x) = x3.
Sie ist an der Stelle 0 nicht differenzierbar.
Beweis: Für die Folge
xn = 1/n gilt
(f(xn) - f(0))/(xn - 0) =
n2/3, was für
n ® ¥
klarerweise nicht konvergiert. Daher kann es die in der Definition (1) verlangte Zahl c
nicht geben. Der geometrische Grund für dieses Verhalten wird klar, wenn Sie sich den
Graphen von f ansehen (z.B. indem Sie den Ausdruck
(abs(x)/x)*abs(x)^(1/3) in den Funktions-Plotter eingeben):
Er besitzt zwar im Punkt (0, 0) eine Tangente, aber diese ist "vertikal", hat also keinen endlichen
Anstieg.
Beispiel 2: Die Betragsfunktion f(x) = |x| ist an der Stelle
0 nicht differenzierbar.
Für jede von oben (d.h. von rechts = von positiven Werten) gegen 0 konvergierende
Folge (xn) ist die linke Seite der Formel
(1) gleich 1, für jede von unten (d.h. von links = von negativen Werten)
gegen 0 konvergierende Folge ist sie gleich -1,
und für Folgen, wie zwischen positiven und negativen Werte oszillieren, existiert der
Grenzwert nicht. Daher kann es die in der Definition (1) verlangte Zahl c
nicht geben. Der geometrische Grund dafür ist hier der Knick im Graphen
(geben Sie abs(x) in den Funktions-Plotter ein),
der die Existenz einer (eindeutigen) Tangente im Punkt (0, 0)
verhindert.
| | | |
| |
| | |
Eine präzise Definition der Differenzierbarkeit ist aber nicht nur
für praktische Rechnungen wichtig, sondern auch, um mathematische Aussagen,
in denen die Ableitung vorkommt (wie z.B. die in einem früheren Kapitel diskutierte
Regel von de l'Hospital) verlässlich beweisen bzw. die genauen
Voraussetzungen, unter denen sie gelten, angeben zu können .
Rechts- und linksseitige Ableitung
Manchmal möchte man zwar die Formel (1) beibehalten, aber nur Folgen betrachten,
die sich von "oben" (d.h. von "rechts") oder von "unten" (d.h. von "links") an
x annähern. Zudem kann
der Definitionsbereich von f
ein Intervall und x eine
Randstelle dieses Intervalls sein. Dann gibt es keine Umgebung von
x, die ganz im Definitionsbereich
von f läge, und
die obige Konstruktion ist genau genommen nicht möglich.
Für solche Situationen definiert man die rechtsseitige (linksseitige)
Differenzierbarkeit wie oben, mit dem einzigen Unterschied, dass
J auf ein
Intervall der Form
(x, x + a)
bzw.
(x - a, x)
eingeschränkt wird. Die Aussage
xn Î J,
die in der Definition vorkommt, bedeutet dann im ersten Fall, dass die Folge
(xn)
von oben (d.h. von rechts) gegen x konvergiert,
im zweiten Fall, dass sie von unten (d.h. von links)
gegen x konvergiert.
Wenn der Grenzwert (1) für alle diese
rechtsseitigen (linksseitigen) Folgen existiert, nennt man ihn
rechtsseitige (linksseitige) Ableitung von
f an der Stelle
x.
Beispiel 1:
Die Funktion
f(x) = 1 - x2
wird auf dem abgeschlossenen Intervall [0, 1] betrachtet.
Sie ist - im Sinn von Definition (1)
- im offenen Intervall (0, 1) differenzierbar,
ihre Ableitung ist dort durch
f '(x) = -2x gegeben.
Weiters existiert an der linken Randstelle die rechtsseitige Ableitung und an der rechten Randstelle die linksseitige
Ableitung. Falls wir für diese ebenfalls die
Bezeichnung f ' verwenden,
können wir schreiben: f '(0) = 0 und
f '(1) = -2,
und in diesem Sinn gilt die Formel
f '(x) = -2x
im gesamten abgeschlossenen Intervall [0, 1].
Beispiel 2: Die Wurzelfunktion f(x) = x1/2
ist für alle
x ³ 0
definiert. Sie ist im Sinn der Definition (1)
für alle x > 0
differenzierbar. Die Randstelle x = 0
besitzt keine Umgebung, die ganz im Definitionsbereich läge, daher können wir
an ihr nur nach der Existenz der rechtsseitigen Ableitung fragen
- eine kurze Rechnung zeigt, dass diese nicht existiert.
(Führen Sie die Rechnung selbst durch, indem Sie die Folge
xn = 1/n
verwenden! Was ist der geometrische Grund für dieses Verhalten?)
Beispiel 3: Die Funktion f(x) = x3/2
ist für alle
x ³ 0
definiert. Sie ist im Sinn der Definition (1)
für alle x > 0 differenzierbar. Die Randstelle x = 0
besitzt keine Umgebung, die ganz im Definitionsbereichs läge, daher können wir
an ihr nur nach der Existenz der rechtsseitigen Ableitung fragen.
Diese existiert und hat den Wert 0.
Beweis: Ist (xn) eine von rechts gegen 0 konvergierende
Folge (d.h. xn > 0), so gilt
(f(xn) - f(0))/(xn - 0) =
(xn3/2 - 0)/(xn - 0) =
xn1/2,
was für
n ® ¥
gegen 0 konvergiert.
Beispiel 4: Die Betragsfunktion f(x) = |x| ist,
wie oben erwähnt, an der Stelle
0 nicht differenzierbar. Aber sowohl die
rechtsseitige Ableitung (sie hat den Wert 1)
als auch die linksseitige Ableitung (sie hat den Wert -1)
existieren an dieser Stelle.
Besitzt x eine Umgebung, die ganz im Definitionsbereich
von f liegt, und ist f an der Stelle
x differenzierbar, so existiert
auch die rechts- und die linksseitige Ableitung, und beide stimmen mit der Ableitung
überein. Umgekehrt folgt aus der Existenz und Übereinstimmung der rechts- und
linksseitigen Ableitungen an einer Stelle x,
dass f dort differenzierbar ist.
Differenzierbarkeit impliziert Stetigkeit
| | | |

Regel von
de l'Hospital
| |
| | |
Intuitiv gesprochen, erkennt man eine stetige Funktion daran, dass ihr Graph keine Sprungstellen hat.
Da - ebenso intuitiv gesprochen -
der Graph einer differenzierbaren Funktion keine Knicke hat, ist zu erwarten, dass
eine differenzierbare Funktion stetig ist - denn was sollte
der Anstieg des Graphen an einer Sprungstelle sein? Diese Vermutung ist tatsächlich richtig,
auch wenn ein präziserer Begriff der Stetigkeit zugrunde gelegt wird.
| | | |
| |
| | |
Satz: Ist f an der Stelle x
differenzierbar, so ist f dort auch stetig.
Der Beweis dieser Behauptung ist fast trivial: Sei f an der Stelle x
differenzierbar, und sei (xn)
eine Folge reeller Zahlen xn Î J,
die gegen x konvergiert, d.h. für
die
gilt. Dann existiert der Grenzwert (1), und wenn wir die linken Seiten von
(1) und (5) miteinander multiplizieren, ergibt
sich
| |
|
( f(xn)
- f(x)) |
= 0, |
| lim |
| n ® ¥ |
|
(6) |
was auch in der Form
geschrieben werden kann. Das drückt aber gerade die Stetigkeit von
f an der Stelle x
aus: Wann immer eine Folge gegen x konvergiert,
so konvergiert die Folge der Funktionswerte gegen f(x).
Damit ist der Satz bewiesen.
| | | |

Stetigkeit
| |
| | |
Eine Variante des Satzes lautet:
Existiert an einer Stelle die rechtsseitige (linksseitige) Ableitung einer Funktion, so ist diese dort
rechtsstetig (linksstetig). Sie kann genauso bewiesen werden,
mit dem einzigen Unterschied, dass
J auf ein
Intervall der Form
(x, x + a)
bzw.
(x - a, x)
eingeschränkt wird, d.h. dass nur Folgen, die von rechts (links) gegen x konvergieren,
betrachtet werden.
|
| | |

rechts- und linksstetig
| |
| | |
| | | |
Zum Seitenanfang | |
| | |
Wir besprechen nun ein Phänomen, das der Intuition ein bisschen zuwiderläuft: Die Ableitung einer
Funktion - die ja selbst wieder eine Funktion ist -
ist nicht unbedingt stetig. Daher formulieren wir zunächst eine
Definition: Eine in einem offenen Intervall A differenzierbare
reelle Funktion heißt an der Stelle
x Î A
stetig differenzierbar, wenn ihre Ableitungsfunktion an der Stelle
x stetig ist.
Funktionen, die nicht stetig differenzierbar sind, kommen beim Lösen praktischer Aufgaben
selten vor. Um aber den Begriff der Differenzierbarkeit besser zu verstehen, sehen wir uns ein Beispiel an:
Beispiel: Gegeben sei die auf ganz R definierte Funktion
| |
{ |
|
x2
sin(1/x)
|
wenn
x ¹ 0 |
| f(x) = |
| |
0 |
wenn
x = 0. |
|
(8) |
Sehen Sie sich zuerst einmal ihren Graphen an (z.B. im Funktions-Plotter
- geben Sie einfach x^2*sin(1/x) ein und
zoomen Sie sich ein bisschen näher.
Hilfreich ist es auch, gleichzeitig die Graphen von
x^2 und -x^2 anzuzeigen).
Sie oszilliert in der Nähe der Stelle 0 sehr
stark: Da der Sinus auf 1/x angewandt wird,
werden in gewisser Weise alle Oszillationen der Sinusfunktion ins Endliche geholt und häufen sich
nahe 0.
Die Funktion f wird dort aber auch sehr klein - das besorgt der
Faktor x2.
(Er "dämpft" die Oszillationen, wenn man so will). Vergewissern wir uns nun, dass f differenzierbar ist.
Ist x ¹ 0, so berechnen wir
mit Hilfe der Produkt- und der Kettenregel
f '(x) =
2x sin(1/x) -
cos(1/x).
An der Stelle 0 müssen wir gemäß
Definition (1) vorgehen: Sei (xn)
eine Folge reeller Zahlen xn ¹ 0,
die gegen 0 konvergiert.
Dann ist
(f(xn) - f(0))/(xn - 0) =
xn
sin(1/xn).
Da der Sinus-Anteil immer zwischen -1
und 1 beschränkt bleibt, konvergiert diese
Folge der Differenzenquotienten gegen 0,
gleichgültig, welche Folge (xn) man gewählt hat.
Daher ist f überall differenzierbar, und die
Ableitungsfunktion ist durch
| |
{ |
|
2x
sin(1/x)
- cos(1/x) |
wenn
x ¹ 0 |
| f '(x) = |
| |
0 |
wenn
x = 0 |
|
(9) |
gegeben. Sehen Sie sich deren Graphen ebenfalls an! Wie f
oszilliert f ' stark in der Nähe der Stelle
0, wird aber im Gegensatz zu
f nahe 0
nicht klein. Das können wir auch dem Ausdruck (9) ansehen, in dem der
Cosinus-Term nicht mit einer positiven Potenz von x multipliziert vorkommt
und daher ("ungedämpft") zwischen -1
und 1 oszilliert, wenn sich
x an 0
annähert.
f ' scheint also nicht stetig zu sein.
Zum formalen Beweis
betrachten wir die gegen 0 konvergierende Folge
xn = (2pn)-1
und berechnen
f '(xn) =
(pn)-1
sin(2pn) -
cos(2pn) =
-1.
Diese (konstante) Folge konvergiert gegen -1,
was nicht f '(0) ist.
Daher ist f ' an der Stelle
0 unstetig.
Dieses Beispiel zeigt auch, dass der Begriff der "Tangente an den Graphen" seine Tücken
hat. Hätten Sie aufgrund einer Betrachtung des Graphen der Funktion
(8) schließen können, dass er im Punkt (0, 0)
eine wohldefinierte Tangente besitzt und wie groß ihr Anstieg ist?
Versuchen Sie, die Unstetigkeit der Ableitung dieser Funktion vom Standpunkt der "Ableitung als Anstieg der Tangente" zu
verstehen!
|
| | |
| |
| | |
| | | |
Zum Seitenanfang | |
| | |
Nun wenden wir uns einem Extremfall zu, der die geometrische Anschauung noch stärker irritiert als
die oben besprochenen Funktionen, deren Ableitung nicht stetig ist:
Es gibt Funktionen, die zwar stetig, aber an keiner Stelle ihres Definitionsbereichs differenzierbar sind!
Beispiel 1:
Wir gehen von der so genannten Sägezahnfunktion g aus.
Im Intervall
[-1/2, 1/2]
stimmt sie mit der Betragsfunktion überein und wird mit Periode
1 für alle reellen Zahlen fortgesetzt.
Nun betrachten wir nacheinander die folgenden Funktionen:
| | | |

Periode
| |
| | |
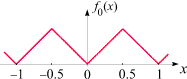 f0(x) = g(x)
f0(x) = g(x)
Das ist die Sägezahnfunktion selbst. Sie ist überall stetig. Ihr Graph besitzt an allen
ganzzahligen Vielfachen von 1/2
(d.h. an den Stellen 0,
±1/2,
±1,
±3/2, ...) Knicke. An diesen Stellen ist
f0 nicht differenzierbar.
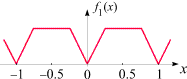 f1(x) = g(x) + g(2x)/2
f1(x) = g(x) + g(2x)/2
Sie kommt zustande, indem eine um den Faktor 2 "verkleinerte" und um denselben Faktor in
x-Richtung "geschrumpfte"
Version der Sägezahnfunktion
zu f0 addiert wird. Ihr Graph besitzt
nun auch an (allerdings nicht allen) ganzzahligen Vielfachen von 1/4
Knicke. Insgesamt liegen die Knickstellen von f1
bereits etwas dichter als jene von
f0.
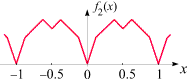 f2(x) = g(x) + g(2x)/2 + g(4x)/4
f2(x) = g(x) + g(2x)/2 + g(4x)/4
Sie kommt zustande, indem eine um den Faktor 4 "verkleinerte" und um denselben Faktor in
x-Richtung "geschrumpfte"
Version der Sägezahnfunktion
zu f1 hinzuaddiert wird. Ihr Graph besitzt
nun auch an (allerdings nicht allen) ganzzahligen Vielfachen von 1/8
Knicke. Insgesamt hat sich die Dichte der Knickstellen im Vergleich zu
f1 erhöht.
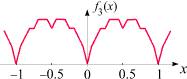 f3(x) = g(x) + g(2x)/2 + g(4x)/4 + g(8x)/8
f3(x) = g(x) + g(2x)/2 + g(4x)/4 + g(8x)/8
Und so geht es nach dem gleichen Schema weiter.
f3 ist an vielen
(allerdings nicht allen) ganzzahligen Vielfachen von 1/16
nicht differenzierbar, f4 besitzt zahlreiche
Knickstellen an ganzzahligen Vielfachen von 1/32, usw.
Nach jedem Schritt liegen die Knickstellen dichter.
| | | |
| |
| | |
Die Funktion, um die es uns geht, ist der Grenzwert von
fn(x) für
n ® ¥,
d.h. die Reihe ("unendliche Summe")
| |
¥ |
|
2-n
g(2n x) . |
|
| f(x) = |
S |
| |
n = 0 |
|
(10) |
Diese Funktion ist für alle reellen Zahlen wohldefiniert und stetig.
Ihren Graphen (siehe Button) können wir uns nicht gut vorstellen, aber dennoch ist er
eine wohldefinierte Punktmenge in der Zeichenebene. Dass die Reihe
für alle x existiert, ergibt sich daraus, dass
g zwischen
0 und 1/2
beschränkt ist und die unendliche Summe über alle
2-n
endlich ist. (Sie hat den Wert 2).
Das liefert eine obere Schranke für die Summen
fn(x), die
auch für große n
nicht überschritten wird. Auf den Beweis der Stetigkeit gehen wir hier nicht ein.
Man kann aber auch zeigen, dass f an keiner Stelle differenzierbar ist.
Intuitiv lässt sich das so verstehen, dass sich die Zahl der Knicke durch jede hinzuaddierte
Version der Sägezahnfunktion erhöht, bis sie schließlich so dicht liegen,
dass dadurch die Existenz jeglicher Tangente an den Graphen verunmöglicht wird.
Die Funktion (10) besitzt übrigens die interessante Eigenschaft der
(näherungsweisen) Selbstähnlichkeit: Wir können die Reihe in der Form
f(x) = g(x) + (1/2) × (g(2x) + g(4x)/2 + g(8x)/4 + ...)
schreiben. Der hervorgehobene Klammerausdruck ist aber nichts anderes als f(2x),
woraus sich ergibt:
Der letzte Term stellt eine um den Faktor 2 "verkleinerte" und um denselben Faktor in
x-Richtung "geschrumpfte"
Version von f dar.
Das bedeutet, dass f
die Summe aus der Sägezahnfunktion g
und einer "kleiner skalierten" Version von sich selbst ist! All die Feinstruktur,
die der Graph von f
aufweist, findet sich in verkleinerter Form in ihm selbst wieder!
Sehen wir ihn uns durch eine Lupe mit Vergrößerungsfaktor 2 an,
so wird er ähnlich aussehen wie nicht vergrößerte Graph, und
dasselbe gilt bei einer weiteren Vergrößerung um den Faktor 2
usw. Eine Punktmenge mit dieser Eigenschaft nennen wir ein (selbstähnliches) Fraktal.
Hier haben wir einen schönen Unterschied zwischen den Graphen
überall differenzierbarer und nirgends differenzierbarer Funktionen.
Während sich erstere unter genügend starker Vergrößerung
kaum von Geraden unterscheiden, werden an letzteren auch bei fortwährendem "Näherzoomen"
immer wieder neue Strukturen sichtbar, die die Existenz von Tangenten verhindern.
Beispiel 2: Nach einem ganz ähnlichen Strickmuster wird eine andere (auf Karl Weierstraß zurückgehende)
stetige, aber nirgends differenzierbare Funktion konstruiert. Wir verzichten auf eine ausführliche Herleitung und
schreiben sie einfach als Reihe hin:
| |
¥ |
|
2-n/2
sin(2n x) . |
|
| w(x) = |
S |
| |
n = 0 |
|
(12) |
Ihre Bestandteile, die Funktionen
2-n/2
sin(2n x),
sind überall differenzierbar, und ihr Graph (genauer: der Graph einer Summe bis zu einem
großen aber endlichen n, wie er auf einem
Bildschirm oder Blatt Papier gerade noch dargestellt werden kann) sieht atemberaubend aus:
Geben Sie nacheinander die ersten drei dieser Summen
- sin(x)
- sin(x) + 2^(-1/2)*sin(2*x)
- sin(x) + 2^(-1/2)*sin(2*x) + 2^(-1)*sin(4*x)
und dann den Ausdruck für die siebente Summe
(mit Kopieren & Einfügen) in den Funktions-Plotter ein!
Sehen Sie sich auch den zuletzt addierten Beitrag
2^(-3)*sin(64*x) an!
Auch die Funktion (12) genügt einer zu (11) analogen
Beziehung
| w(x) = sin x + 2-1/2 w(2x) , |
|
(13) |
die erweist, dass ihr Graph ein selbstähnliches Fraktal ist.
| | | |

Reihen
| |
| | |
Im Applet rechts können Sie das schrittweise Entstehen der Graphen dieser beiden
Beispiele mitverfolgen.
Dass die Differenzierbarkeit einer Funktion durch deren Stetigkeit nicht garantiert ist, wurde erst im
19. Jahrhundert erkannt. Aus der geometrischen Anschauung
heraus glaubte man lange Zeit, dass der Graph einer stetigen Funktion
überall (außer in einzelnen isolierten Punkten) eine Tangente besitzt.
Erst durch die Präzisierung der Begriffe Stetigkeit und Differenzierbarkeit
und durch die Konstruktion von Beispielen wie den beiden gerade vorgeführten,
wurden diese Irrtümer erkannt.
|
| | |
Applet
Nirgends
differenzierbare
Funktionen
| |
| | |
| | | |
Zum Seitenanfang | |
| | |
In diesem Kapitel haben wir nur reelle Funktionen untersucht, d.h. solche, deren Definitions- und Wertebereich
Teilmengen der Menge der reellen Zahlen sind.
Die Begriffe der Differenzierbarkeit und der Ableitung können aber in mehrfacher Hinsicht
auch auf andere Klassen von Funktionen verallgemeinert werden.
Einige dieser Verallgemeinerungen werden in anderen Kapitel zumindest gestreift.
- Für Funktionen in mehreren Variablen lässt sich auf
natürliche Weise eine Verallgemeinerung des Ableitungsbegriffs definieren:
Die partiellen Ableitungen einer Funktion
f º f(x, y)
werden berechnet, indem eine Variable konstant gehalten und nach der anderen differenziert wird.
- Im Rahmen der komplexen Zahlen ergibt sich ein Differenzierbarkeitsbegriff, der sich vom
hier besprochenen erheblich unterscheidet. Er führt auf den Begriff der analytischen Funktionen.
- In der Variationsrechnung wird die Ableitung zur so genannten Funktionalableitung verallgemeinert, d.h.
für Funktionen, die auf Mengen von Funktionen definiert sind.
- In der Konstruktion zahlreicher anderer mathematischer Strukturen und Räume
(wie zum Beispiel der so genannten verallgemeinerten Funktionen) spielt die Idee der
Ableitung eine wichtige Rolle.
- Die kovariante Ableitung von Objekten, die "Tensoren" genannt werden und Verallgemeinerungen von Vektoren
darstellen, ist für die moderne Physik unverzichtbar geworden.
In den meisten dieser Gebiete werden die Differenzierbarkeitseigenschaften reeller Funktionen
und der Zusammenhang mit dem Stetigkeitsbegriff benutzt. Was wir in diesem Kapitel besprochen haben,
steht also Pate für zahlreiche Weiterentwicklungen der Mathematik.
| | | |
partielle Ableitung
(in Vorbereitung)

analytische Funktionen

Funktionalableitung
(in Vorbereitung)
verallgemeinerte
Funktionen
(in Vorbereitung)
kovariante Ableitung
(in Vorbereitung)
| |
| | |
Zuletzt sei noch erwähnt, dass im Fall von Funktionen, die auf diskreten Mengen (auf endlichen
Mengen oder auf der Menge der natürlichen Zahlen) definiert sind, die Differenzenquotienten
einen gewissen Ersatz für die Ableitung darstellen. Die mit ihrer Hilfe formulierten
Differenzengleichungen werden häufig dazu benutzt, um
dynamische Prozesse zu modellieren und zu simulieren.
|
| | |

Differenzengleichungen
(in Vorbereitung)
| |