Orthogonalität von Vektoren und orthonomierte Basen von Vektorräumen Andreas Pester Fachhochschule Techikum Kärnten, Villach
pester@cti.ac.at Zusammenfassung: In diesem Abschnitt wir der Begriff der Orthogonalität und einer orthonormierten Basis erläutert

Hauptseite

Stichworte: Defintion | Orthonormierte Basis | Theoreme

Zwei Vektoren u und v heißen orthogonal zu einander, wenn ihr Skalarprodukt u · v = 0  bzw. u^T · v = 0 Null ist.

Zwei Unterräume  V und W des Vektorraumes heißen orthogonal zu einander, wenn jeder Vektor v aus V und jeder Vektor w aus W  orthogonal zu einander sind, d.h. ihr Skalarprodukt  v · w = 0  bzw. v^T · w = 0  sind.

1. Die x,y-Ebene bildet einen Unteraum  V von R³ (zweidimesional), die z-Achse einen eindimesionalen Unterraum W. Das Skalarprodukt von beliebigen zwei Vektoren aus V bzw. W ist Null, da sie senkrecht zueinander stehen. D.h., die Unterräume V und W sind orthogonal zueinander.
2. Die x,y-Ebene bildet einen Unteraum  V von R³ (zweidimesional), die x,z-Ebene bildet auch einen zweidimensionalen  Unterraum W . Es sieht so aus, als ob beide Unterräume ebenfalls orthogonal zu einander sind, aber das stimmt nicht . Der Vektor v = (1,1,0)^T liegt in der x.y-Ebene, der Vektor w = (1,0,1)^T liegt in der x,z-Ebene, aber ihr Skalarprodukt ist v^T · w = 1 ist nicht Null. Das gleiche gilt für den Vektor (1,0,0), der sowohl in der x,y- als auch in der x,z-Ebene liegt und nicht orthogonal zu sich selbst ist.
3. Wenn ein Vektor in zwei orthogonalen Unterräumen gleichzeitig enthalten ist, so muss er zu sich selbst orthogonal sein, d.h. v ^T· v = 0  bzw. v ·v = 0  . Das trifft auf den Nullvektor zu, der in jedem Unterraum enthalten ist. Der Vektor (0,0,0)^T liegt z.B. in der x,y- und der x,z-Ebene.

Die Vektoren q_1,q₂, ...,q_n sind orthonormiert wenn, folgende Bedingung erfüllt ist:

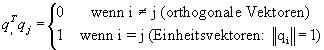
Eine Matrix mit orthonormalen Spalten wird mit Q bezeichnet und orthogonale Matrix genannt.

• Für eine orthogonale Matrix gilt : Q^T·Q = I
• Wenn Q orthonogonal ist , so lässt Abbildung Qx die Länge eines Vektors und das Skalarprodukt unverändert:
  • ||Qx||=||x|| für jeden Vektor x
  • (Qx^)T·(Qy) = x^T(Q^T· Q)y = x^T·y

1. Die Rotationsmatrix D, die die Rotation eines Vektors in der Ebene um den Winkel f beschreibt, is eine orthogonale Matrix:
   
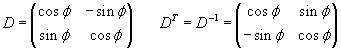
   somit gilt D·D^T = 1. Die Spalten von D bilden eine orthonormale Basis für den R² .
2. Jede Permutationsmatrix ist orthogonal
3. Die Reflexionsmatrix Q = I - 2u·u^T ist orthogonal (und symmetrisch), wenn ||u||=1

Wie konstruiert man zu n linear unabhängigen Vektoren im Rⁿ eine orthonormierte Basis ? → Gram-Schmidt-Prozess