
 |
| Hyperbelfunktionen |
| H 1. Grundlegende Definitionen und Motivation |
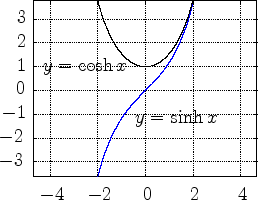
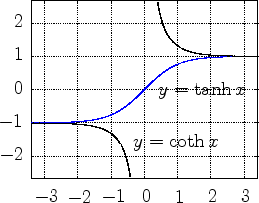
| H 2. Namenspatronanz: Wieso Hyperbelfunktionen? |
|
| H 3. Quell- und Zielmengen des hyperbolischen Cosinus und des hyperbolischen Sinus - Stetigkeit |
| H 4. Die Umkehrfunktionen der Hyperbelfunktionen: Areafunktionen |



|