

Interpolationsverfahren
Informatikprojekt
Fachhochschule Technikum Kärnten
Betreuer
Andreas Pester
![]()
Harald Habiger ![]()
Studenten
Sonja Moschik ![]()
Daniel Kendler ![]()
in Zusammenarbeit mit dem Projekt "Neue Medien in der Mathematik-Ausbildung".
Links: Applet | Theorie | Hilfe zur Bedienung des Applets
Die Aufgabe der Interpolation ist es, durch gegebene Stützpunkte (xi, yi) i = 1,...,n eine geeignete Kurve zu legen und somit Funktionswerte zwischen der kleinsten und grö?ten Stützstelle x0 und xn zu bestimmen.
Gegeben seien (n+1) Stützpunkte (z.B. Messwerte)
y0 = f(x0), y1 = f(x1), ... yn = f(xn).
Gesucht wird ein Polynom n-ten (oder weniger) Grades, dass die Interpolationsbedingung
pn(x0) = y0 , pn(x1) = y1, ... pn(xn) = yn
erfüllt.
pn nennt man Interpolationspolynom, x0, x1, ... xn sind die Stützstellen und y0, y1, ... yn die Stützwerte.
Eindeutigkeit: Zu beliebigen Stützpunkten (xi, yi) (i = 0,1, ... n) mit paarweise verschiedenen Stützstellen xi ≠ xj für alle i ≠ j existiert genau ein Interpolationspolynom pn vom Grad ≤ n mit pn(xi) = yi für 0 ≤ i ≤ n.
Newton Interpolation
Der Ansatz für das Newton Interpolationspolynom für n+1 Stützstellen lautet
pn(x) = α0 + α1(x - x0) + α2(x - x0)(x - x1) + α3(x - x0)(x - x1)(x - x2) + ... + αn(x - x0)(x - x1) ... (x - xn-1)
Die Forderung pn(xi) = yi (0 ≤ i ≤ n) ergibt ein Gleichungssystem der Form
y0 = α0
y1 = α0 + α1(x1 - x0)
y2 = α0 + α1(x2 - x0) + α2(x2 - x0)(x2 - x1)
...
yn = α0 + α1(xn - x0) + ... + αn(xn - x0)(xn - x1) ... (xn - xn - 1)das schrittweise von oben nach unten gelöst wird
α0 = y0; α1 = (y1 - y0)/(x1 - x0); ...
Es kann gezeigt werden, dass der Koeffizient αk gleich der k-ten dividierten Differenz ist. Dadurch ergibt die Rekursionsformel
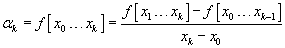
Die Auswertung der Rekursionsformel erfolgt am zweckmäßigsten im Schema der dividierten Differenzen
x0 f [x0] f [x0,x1] x1 f [x1] f [x0,x1,x2] f [x1,x2] f [x0,x1,x2,x3] x2 f [x2] f [x1,x2,x3] f [x0,x1,x2,x3,x4] f [x2,x3] f [x1,x2,x3,x4] x3 f [x3] f [x2,x3,x4] f [x3,x4] x4 f [x4] Das Schema wird spaltenweise unter Anwendung folgender Formeln berechnet
f [x0,x1] = (f [x1]-f [x0])/(x1- x0); f [x1,x2] = (f [x2]-f [x1])/(x2- x1); ...
f [x0,x1,x2] = (f [x1,x2]-f [x0,x1])/(x2 -x0); ...Die gesuchten Koeffizienten αk des Interpolationspolynom findet man in der ersten Schrägzeile des Schemas.
Vorteil: Wird zu den vorhandenen Punkten ein weiterer Punkt xn + 1 (> xn) hinzugefügt, braucht das vorhandene Differenzschema nur um eine weitere untere Schrägzeile ergänzt werden.
Lagrange Interpolation
Eine andere Möglichkeit der Erhaltung des Interpolationspolynoms basiert auf einer alternativen Darstellung der Polynome. Mit dem Lagrange Ansatz können die Koeffizienten direkt aus den Stützstellen berechnet werden.
Definition: Seien i, j zwei Zahlen. Dann ist
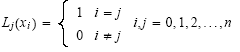
Nun betrachten wir die zu den Stützstellen {x0,..., xn} zugehörigen Lagrange-Polynome. Für alle 0 < i < n definieren wir.
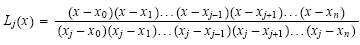
Nun stellen wir das Interpolationspolynom p(x) als
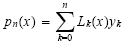
dar.
Vorteile:
Das Polynom löst die Aufgabe eindeutig.
Die Koeffizienten des Polynoms sind explizit von den Stützstellen abhängig.
Das Polynom hängt linear von den yj ab.Nachteile:
Der Rechenaufwand für die Polynome ist sehr hoch.
Der Übergang von pn(x) zu pn+1(x) ist unübersichtlich.Cubic Splines
Eine kubische Splinefunktion p(x) ist durch die folgenden Eigenschaften definiert.
Gegeben sind n + 1 Stützpunkte (x0, y0), (x1, y1), ... ; (xn, yn), 2 ≤ n.
1. p(x) ist in jedem Intervall [xi, xi+1], i = 0,1, ... , n-1
2. pi(xi) = yi für i = 0,1, ... , n
3. p(x) ist Überall in [x0; yn] zweimal stetig differenzierbar.Das bedeutet:
Wir haben also 4n Unbekannte
und folgende Gleichungen:
Das sind insgesamt 4n - 2 Gleichungen. Wir müssen daher zwei weitere Bedingungen wählen. Diese Wahl soll einerseits dazu dienen, dieses Gleichungssystem in eine lösbare Form überzuführen, andererseits soll das Ergebnis so wenig wie möglich beeinflusst werden. Dabei bieten sich folgende Möglichkeiten:
1. Natürliche Randbedingung: Am Anfangs- und am Endpunkt Krümmung = 0 setzen.
Dadurch erhält man ein Spline, das sich wie eine biegsame Latte verhält.
2. "Not a knot condition" von de Boor: Dabei wird über die beiden ersten Intervalle dasselbe Polynom dritten Grades verwendet.
3. Periodische Randbedingung: Gleichsetzten der ersten und zweiten Ableitung an der ersten und der letzten Stelle.
Nach der Wahl einer dieser Methoden stehen somit 4n Gleichungen zur Verfügung. Genügend um das System eindeutig zu lösen.
Nachdem das Gleichungssystem aufgelöst ist, können die Lösungen in die ursprünglichen Polynom-Gleichungen eingesetzt werden. Als Resultat erhält man die Gleichungen für die einzelnen Teilstücke zwischen den Wertepaaren.
Im Zeichenfenster können die Stützpunkte (1) durch klicken mit der linken Maustaste oder durch das eingeben der Koordinaten in (2) platziert werden. Befindet sich der Mauszeiger auf einem Stützpunkt, so kann dieser durch gedrückt halten der linken Maustaste verschoben werden. Durch das Betätigen der rechten Maustaste auf einen bestehenden Stützpunkt, kann dieser wieder entfernt werden.
In (3) kann das Interpolationsverfahren aufgewählt werden. Bei der Newtoninterpolation kann durch anklicken von (4) ein zusätzliches Fenster angezeigt werden.
In diesem Fenster wir das Schema der dividierten Differenzen angezeigt. Verändern sich die Punkt auf der Zeichenfläche, so werden die Werte die für das Dreieck neu berechnet werden müssen in Rot geschrieben.
Durch das Anklicken von (5) kann das folgende Fenster zur Lagrangeinterpolation geöffnet werden.
Beide Fenster beinhalten einen Button, der es ermöglicht zwischen den Ansatz von Newton bzw. Lagrange und den ausmultiplizierten Polynom umzuschalten. Der Button ändert dabei seine Beschriftung.
In (1) kann das Intervall der x- bzw. y-Achse zwischen -10 und 10, sowie die Auflösung (zwischen Länge des Intervalls und 1/10 davon) angegeben werden.
Mit der Checkbox Grid kann ein Raster aktiviert bzw. deaktiviert werden. Die Feinheit des Raster ist von der Auflösung abhängig.
Wird die Checkbox Cursor aktiviert, so werden in der linken unteren Ecke der Zeichenfläche (2) die Koordinaten der aktuellen Mausposition angezeigt.
Ist die Checkbox Memory aktiviert so wird beim Löschen oder beim Einfügen eines neuen Stützpunktes, sowie beim Verschieben eines Punktes, zusätzlich zur neu entstehenden Kurve auch die vorige gezeichnet. Es können 5 Kurven pro Interpolationsverfahren gezeichnet werden. In (3) wird die Anzahl der gespeicherten Kurven angezeigt.
Mit Autoscale werden die Achsen so skaliert, dass die Kurven in der Zeichenfläche vollständig sichtbar ist.Fragen
Falls Sie weitere Fragen zum Applet haben, uns Hinweise auf Fehler oder Kommentare zukommen lassen wollen, schreiben Sie uns bitte.