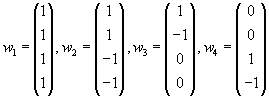
Die Wavelet-Basis Andreas Pester Fachhochschule Techikum Kärnten, Villach
pester@cti.ac.at Zusammenfassung: In diesem Abschnitt wird die Basis für Wavelets im R⁴ eingeführt und der dazugehörige Basiswechsel dargestellt

Hauptseite

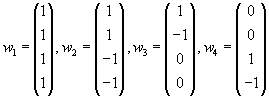
Dies sind die Basis-Vektoren der diskreten Wavelet-Transformation (DWT) im vierdimensionalen Raum. Unter Wavelets versteht man "kleine" Wellen. Sie haben unterschiedliche Länge und sind an unterschiedlichen Plätzen plaziert.  Nur der erste Vektor ist eigentlich kein Wavelet, sondern ein flacher Vektor (für den Hintergrund). Die Wavelet-Transformation hat Ähnlichkeiten mit der Fourier-TRansformation

Die Wavelet-Basisvektoren sind orthogonal, aber nicht orthonormiert. w₃ ist in der ersten Hälfte des Raumes plaziert, w₄ in der zweiten Hälfte des Raumes, c₃ enthält Informationen über die erste Hälfte von v, c₄ über die zweite Hälfte von v.

Die Wavelet-Basis wird eingesetzt um diskrete Signale, die als Vektoren im Rⁿ (n=2^m - Breite des Eingangssignals) aufgefasst werden, zu koprimieren. Realistisch ist ein n über 10.000, aber zur Demonstration wählen wir n = 4. Ca. 5 % der größten Koeffizienten bleiben bei einer derartigen Transformation  (lossless) übrig. Den Kompressionsteil  stellen wir hier nicht dar, da er wesentlich über den Bereich der Mathematik hinausgeht.

Es sei v = (6 2 5 -1)^T . Damit die neuen Koordinaten c berechnet werden können, stellen wir zuerst v in der neuen Basis dar:

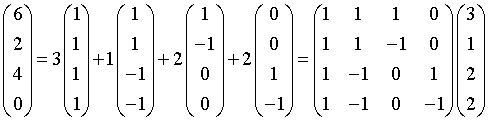
c = W^-1·v. Man muss also die inverse von W bestimmen. Dazu erinnern wir uns, dass die Spalten von W orthogonale Vektoren sind. Man kann also schreiben W^-1 = W^-1·(W^T)-1·W^T = (W^T·W)^-1·W^T. Der erste Faktor ist eine Diagonalmatrix, die sehr einfach zu invertieren ist. Der zweite Faktor, die transponierte Matrix W^T, lässt sich ebenfalls leicht bilden. Man erhält:

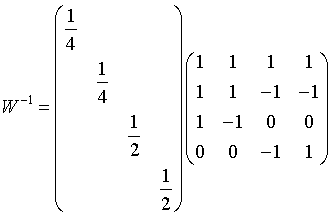
und c = W^-1·v = (3 1 2 2^)T als neue Wavelet-Koeffizienten. Diese sind viel flacher als die ursprünglichen und könnten jetzt zusätzlich noch mit lossy-Verfahren komprimiert werden.