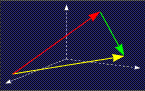
|
|
|
|
|
|
|
| |
| |
|
|
|
|
|
|
|
||
| |
|
|
|
|
|
|
|
||
| |
|
Die Figur zeigt die neue
Strömung, die beim Zusammenfließen zweier Flüsse
ensteht:
rechnerische Addition Die Koordinaten des Summenvektors
erhält man rechnerisch durch:
Die Summe zweier Vektoren
v, w im Raum wird gebildet durch:
|
|
|
|
Applet Vektoren im R³ |
|
||
| |
|
|
|
|
|
|
|||
| |
|
Was könnte die Gleichung z = u - v bedeuten? Nun, u - v ist eine Kurzschreibweise für u + (-v), dh. es wird zum Vektor u der inverse Vektor von v addiert. graphische Subtraktion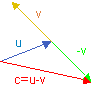 
Zwei Vektoren u und v werden graphisch subtrahiert, indem man den inversen Vektor von v addiert. Den neuentstandenen Vektor c nennt man die Differenz der Vektoren a und b und schreibt c = u - v . rechnerische Subtraktion Den Differenzvektor von a und b erhält man rechnerisch durch: 
Beispiel: 
Die Differenz zweier Vektoren a, b im Raum wird gebildet durch: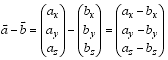 
Beispiel :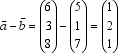 
|
|
|
|
|
|
||
| |
|
|
|
|
|
|
|
||
| |
|
Vektoren v kann man mit einer reelen Zahl, einem sogenanntem Skalar , multiplizieren. Der Vektor xv hat als Repräsentanten Pfeile mit gleicher Richtung und x-facher Länge. graphische Multiplikation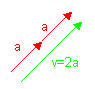 
Beispiel: Führe folgende Vektoraddition durch: v = a + a 
v = 
Man kann erkennen, dass die Richtung von a erhalten bleibt, die Länge sich aber verdoppelt hat. Besser ist daher den Vektor v in der Form: v = 2a zu schreiben. rechnerische Multiplikation 
Beispiel: c = -2 => 
Multiplikation im Raum: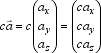 
Beispiel: c= 3 =>
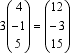
Beispiel: 
=> 
|
|
|
|
|
|||
| |
|
|
|
|
|
|
|
||
| |
|
In den vorigen Kapiteln haben wir die grundlegenden Rechenregeln für Vektoren kennengelernt, aber daraus noch keinen direkten Nutzen gezogen. Nun wollen wir das Erlernte in einer wichtigen Anwendung einsetzen: Sind Richtung und Länge eines Vektors v bekannt, so kann man einen zweiten Vektor w durch Angabe seiner Länge und einem Winkel φ zum ersten Vektor v festlegen: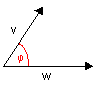 
|
|
|
|
|
|
||
| |
|
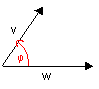
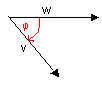
Oft stellt sich die Frage nach der Richtung der Winkelsymmetralen
des von zwei Vektoren gebildeten Winkels. Im Allgemeinen entspricht die Richtung des zugehörigen Additionvektors nicht der Richtung der Winkelsymmetrale, wie man aus dem unteren Beispiel gut erkennen kann: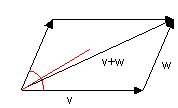 
Besitzen die beiden Vektoren aber die gleiche Länge, so stimmt die Richtung des Additionsvektors mit der Richtung der Winkelsymmetralen überein: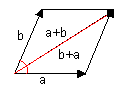 
Die Addition a+b bzw. b+a bildet statt eines Parallelogramms
eine Raute. Der Summenvektor entspricht der Diagonalen der Raute,
welche bekanntlich den Winkel φ. Um die Richtung der Winkelsymmentralen
zu erhalten, benötigt man also zwei Vektoren
gleicher Länge. Da alle Einheitsvektoren die gleiche
Länge besitzen, kann man sie zur Bestimmung der Winkelsymmetralen
zweier Vektoren heranziehen:Richtung der Winkelsymmentralen = 
|
|
|
|
|
|||
| |
|
|
|
|
|
|
|
||
| |
|
Ein weiteres wichtiges Werkzeug der Vektorrechnung ist die Berechnung des Mittelpunkts M einer Strecke: Beispiel: Es ist der Mittelpunkt M der Strecke AB [ A( 2 | 5 ), B( 6 | 1) ] zu bestimmen. Lösung: Fertigen wir zuerst eine Skizze an: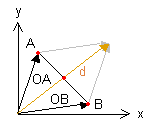 
Addiert man den Ortsvektor OA zum Ortsvektor OB, so erhält man den "Diagonalvektor" d des dargestellten Parallelogramms: d = OA + OB. Wie man aus der Skizze erkennen kann, ist der Ortsvektor OM des Mittelpunkts der halbe Diagonalvektor. Somit erhalten wir folgende Formel zur Berechung des Mittelpunkts M: 
Eine weitere Möglichkeit zur Bestimmung des Mittelpunkts wäre: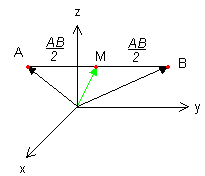 
Man addiert zum Ortsvektor OA den halben Vektor AB. Der Summenvektor ist der Ortsvektor OM, der zum Mittelpunkt M von AB zeigt. 
|
|
|
|
|
|
||
| Teilungspunkt einer Strecke
|
|
||||||||
Betrachten wir die Punkte A,B und T1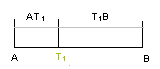 
AT1 ist halb so lang wie BT1, man sagt: " T1 teilt die Strecke AB innen im Verhältnis 1:2 ". Eine weiter Situation: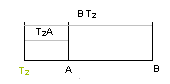 
AT2 ist wieder halb so lang wie BT2, man sagt: " T2 teilt die Strecke AB außen im Verhältnis 1:2 ". |
|||||||||
Beispiel: 
Beispiel: 