|
|
|
|
|
|
| |
|
|
|
|
|
||
| |
|
|
|
|
|
|
|
| |
Der Name Vektor kommt aus dem Lateinischen und heißt soviel wie "Träger" oder "Fahrer". Eine orientierte Strecke, die den kürzesten Weg zwischen einem beliebigen Weg-Anfangspunkt A und einem beliebigen Weg-Endpunkt E angibt wird Pfeil AE genannt. Symbolisch: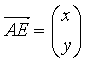 
= (x/y) oder 
Zeilenform Spaltenform Ihr seht also, wenn man von Vektoren spricht und diese auch symbolisch schreiben will, wird über die Buchstaben einfach ein Pfeil geschrieben. Dieses angegenbene geordneten Zahlenpaar in der Ebene bzw. Zahlentripel im Raum heißt kartesische Koordinatendarstellung des Pfeiles. Wichtig dabei ist auf die Orientierung zu achten, das heißt in welche Richtung der Pfeil läuft (Richtungspfeil). Grundaufgaben für das Rechenen mit Punkten und Pfeilen: Sind die Koordinaten der Punkte A und E gegeben und will man nun die Koordinaten von AE wissen, geht man in der Ebene folgendermaßen vor: xAE = xE - xA yAE = yE - yA , daraus ergibt sich die: "Spitze minus Schaft Regel" AE = E - A Zur Berechnung von Pfeilen im Raum verwendet man die gleiche Formel, jedoch kommt noch die z-Koordinate dazu: xAE = xE - xA yAE = yE - yA zAE = zE - zA, daraus ergibt sich die: "Spitze minus Schaft Regel" AE = E - A Sind nun umgekehrt die Koordinaten von A und AE gegeben erhält man die Koordinaten von E in der Ebene so: xE = xA + xAE yE = yA + yAE , daraus ergibt sich die: "Append" - Regel E = A + AE Im Raum geht man analog vor nur mit Hinzunahme der z-Koordinate: xE = xA + xAE yE = yA + yAE zE = zA + zAE , daraus ergibt sich die: "Append" - Regel E = A + AE Betrachtet man nun diese Pfeile, so kann man erkennen, dass verschiedene Pfeile die gleiche Koordinatendarstellung besitzen. 
Man kann sehen, dass durch die Angabe der Koordinatendarstellung nicht ein Pfeil, sondern die Menge aller Pfeile, die gleichlang, gleichorientiert und parallel sind, gegeben ist. Die Anzahl dieser Pfeile ist unendlich. Durch diese Tatsache, kann man nun einen Vektor definieren: Definition: Die Menge aller Pfeile der Ebene bzw. des Raums, welche gleichlang, parallel und gleichorientiert sind, wird als Vektor bezeichnet. Also anders ausgedrückt kann man sagen, dass ein Vektor die Menge all jener Pfeile der Ebene oder des Raumes ist, welche das gleiche geordnete Zahlenpaar bzw. das gleich geordnete Zahlentripel als Koordinaten besitzen. Ein Pfeil beschreibt also die geraglinige Bewegung eines Punktes, ein Vektor hingegen die geradlinige Bewegung einer Punktmenge. Kurz gesagt, ein Vektor beschreibt eine Schiebung. Somit ist die Schiebung eines Vektors ortsunabhängig, wobei die Schiebung eines Pfeiles ortsabhängig ist. Um mit diesen vielen Regeln
und Begriffen umgehen zu lernen, ist es ratsam die folgenden Beispiele zu
probieren. |
|
|
|
|
|
|
| |
Beispiel: Gegeben sind der Anfangspunkt A und der Endpunkt
E eines Pfeiles. Ermittle seine Koordinatendarstellung graphisch und
rechnerisch: a) A(3/2), E(6/5) b) A(-1/2), E(3/-4) c) A(0/0), E(4/3) Beispiel: Gegeben
sind der Anfangspunkt A und die Koordinatendarstellung des Pfeiles AE.
Ermittle die Koordinaten seines Endpunktes E graphisch und rechnerisch
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
| |
Für viele Anwendungen ist es notwendig die Länge eines Pfeiles auszurechnen, so zum Beispiel das Berechnen von Vielecken in einem Koordinatensystem. Die Länge eines Pfeils ergibt sich unter der Anwendung des Pythagoreischen Lehrsatzes.: 
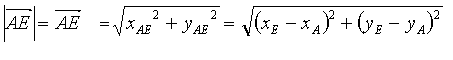bzw.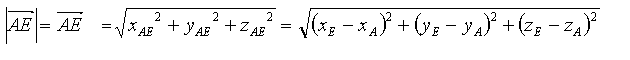 
Die Länge eines Vektors 
wird auch als Betrag 
eines Vektors bezeichnet und lässt sich in der Ebene
bzw. im Raum folgendermaßen errechnen:
Dise Formeln wirken vielleicht etwas kompliziert, doch um besser damit umgehen zu können, seht ihr unten ein durchgerechnetes Beispiel: Ermittle den Umfang des Dreiecks A(2/1), B(5/4), C(0/3) graphisch und rechnerisch. Lösung: 
= (3/3) => 
= c = 
= 4,24
= (-5/-1) => 
= a = 
= 5,10
= (2, -2) => 
= b = 
= 2,83U = a + b + c = 12,17 Nun könnt ihr es selbst probieren: Beispiele: 1)Ermittle den Umfang des Vielecks graphisch und rechnerisch: a) A(3/3), B(-2/2), C(-3/-3), D(3/-1) b) A(3/1), B(0/4), C(-2/4), D(-4/2), E(0/-3) 2)Wie kann die fehlende Koordinate des Pfeils gewählt werden, damit er die angegebene Länge l besitzt? a)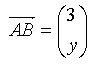 
l=5b) 
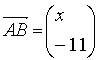l=613) Ermittle den Betrag des Vektors 
a)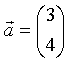 
b)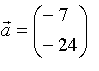 
c)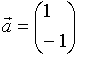 
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
| |
Hat
man sich nun etwas mit den vorigen Kapiteln auseinandergesetzt, so kann man
erkennen, dass nicht alle Vektoren von der gleiche Art sind. Einige gehen
zum Beispiel immer vom Nullpunkt aus, andere wiederum gehen gerade in die
entgegengesetzte Richtung und wieder andere sind Null. Daraus ergeben sich
die folgenden Definitionen: Ortsvektor: Ein Vektor, der den kürzesten Weg vom Ursprung O zum Punkt P beschreibt, wird Ortsvektor 
genannt.Richtungsvektor: Im Mathematikunterricht wird größtenteils mit Richtungsvektoren gerechnet. Wichtig ist dabei zu wissen, dass es bei Richtungsvektoren - wie der Name schon sagt - auf die Richtung ankommt, in die der Vektor verläuft. Ebenfalls wichtig ist zu wissen, was der Unterschied zu einem Ortsvektor ist. Inverser Vektor Der Vektor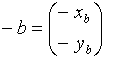 
bzw.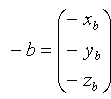 
heißt entgegengesetzter oder inverser Vektor des Vektors 
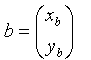bzw.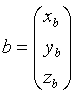 
Nullvektor Die Vektoren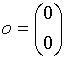 
bzw.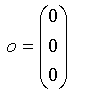 
heißen Nullvektoren.Einheitsvektor: Der zum Vektor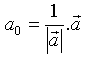
parallele (kollineare) Vektor 
heißt Einheitsvektor des Vektors
. Er hat immer den Betrag 1. |