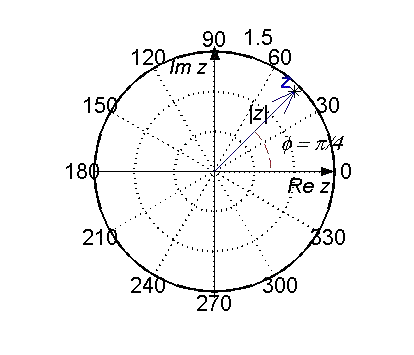
 Daraus ergeben sich folgende Zusammenhänge :
Re z = |z|·cos(f)
Daraus ergeben sich folgende Zusammenhänge :
Re z = |z|·cos(f)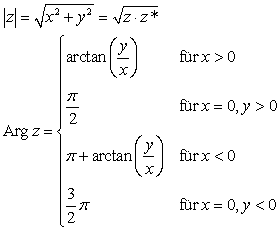
| z = -4 + 3i = 5·(cos(2.498091545)+i·sin(2.498091545)), |z| = 5 , Arg z = 2.498091545 |
| z = 0 hat |z| = 0 und Arg z beliebig |
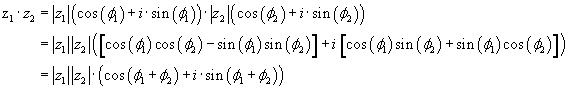
 Beispiel 3: Es seien z1 = 1+i, |z1| =
Ö2 und Arg z1=p/4,
z2 = -Ö2, |z2| =
Ö2 und Arg z2=p gegeben,
dann gilt z1*z2=Ö2*Ö2*(cos(p/4+p)+i*sin(p/4+p))
= 2*(cos(5p/4)+i*sin(5p/4))
= 2*(-Ö2/2-Ö2/2*i)
= -Ö2-Ö2i
Kurze Denkaufgabe:
Beispiel 3: Es seien z1 = 1+i, |z1| =
Ö2 und Arg z1=p/4,
z2 = -Ö2, |z2| =
Ö2 und Arg z2=p gegeben,
dann gilt z1*z2=Ö2*Ö2*(cos(p/4+p)+i*sin(p/4+p))
= 2*(cos(5p/4)+i*sin(5p/4))
= 2*(-Ö2/2-Ö2/2*i)
= -Ö2-Ö2i
Kurze Denkaufgabe:
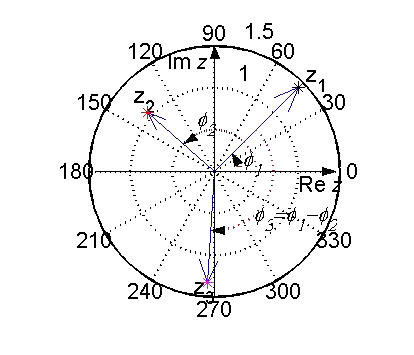
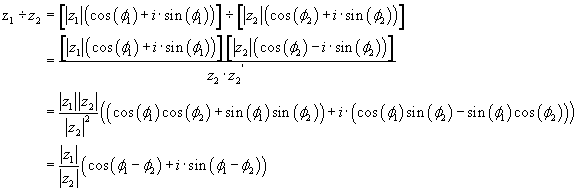 Geometrisch läßt sich das Ergebnis der Division als die Drehung des Vektors der Zahl z1 um den Winkel Arg z2
in mathematisch negativer Richtung deuten. Der Länge des Ergebnisvektors ist das Ergebnis der Division von
|z1|/|z2|.
Geometrisch läßt sich das Ergebnis der Division als die Drehung des Vektors der Zahl z1 um den Winkel Arg z2
in mathematisch negativer Richtung deuten. Der Länge des Ergebnisvektors ist das Ergebnis der Division von
|z1|/|z2|.
 Beispiel 4: Es sei z = 3·(cos(p/2)+i·sin(p/2)).
Dann gilt für w=1/z a) |w| = 1/3 , b) Arg w = -p/2
Kurze Denkaufgabe: Welche komplexe Zahl ist das Spiegelbild von z ¹ 0 bei Spiegelung
Beispiel 4: Es sei z = 3·(cos(p/2)+i·sin(p/2)).
Dann gilt für w=1/z a) |w| = 1/3 , b) Arg w = -p/2
Kurze Denkaufgabe: Welche komplexe Zahl ist das Spiegelbild von z ¹ 0 bei Spiegelung