Die komplexe Exponentialfunktion ez
Andreas Pester
Fachhochschule Techikum Kärnten, Villach
pester@cti.ac.at
Zusammenfassung: In diesem Abschnitt werden die wichtigsten arithmetischen und Abbildungseigenschaften
der komplexen Exponentialfunktion behandelt. Er dient zur Ergänzung für Studenten nicht-mathematischer Fachrichtungen,
die sich mit elementaren komplexen Funktionen beschäftigen.
Stichworte:
Defintion |
Arithmetische Eigenschaften |
Periodizität |
Abbildungseigenschaften |
Formel 1 |
Formel 2 |
Abbildung 1 |
Abbildung 2
Die Definition der komplexen Exponentialfunktion ez ist eine
Erweiterung der Defintion der Exponentialfunktion für reelle Argumente.
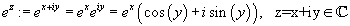 Daraus ergeben sich die Bestimmungen für Real-, Imginärteil, Betrag und Argument
Daraus ergeben sich die Bestimmungen für Real-, Imginärteil, Betrag und Argument
Re ez = excosy, Im ez = exsiny ,
|ez| = ex und Arg ez = y.
Die wichtigsten Eigenschaften für Exponentialfunktionen gelten auch im Komplexen, wie z.B.:
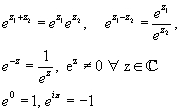 Eine Eigenschaft ist besonders wichtig, da sie die komplexe von der reellen Exponentialfunktion
unterscheidet - die Periodizität.
Für die komplexe Exponentialfunktion gilt folgende Eigenschaft:
Eine Eigenschaft ist besonders wichtig, da sie die komplexe von der reellen Exponentialfunktion
unterscheidet - die Periodizität.
Für die komplexe Exponentialfunktion gilt folgende Eigenschaft:
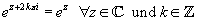 Dies ergibt sich aus folgendem Zusammenhang:
Dies ergibt sich aus folgendem Zusammenhang:
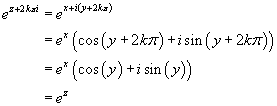 Die Periode der komplexen Exponentialfunktion beträgt 2pi. Diese Eigenschaft gibt es
im Reellen nicht.
Die Abbildung w = ez hat folgende Eigenschaften:
Die Periode der komplexen Exponentialfunktion beträgt 2pi. Diese Eigenschaft gibt es
im Reellen nicht.
Die Abbildung w = ez hat folgende Eigenschaften:
|
Die Gerade
|
x = x0 |
wird auf den Kreis um 0 mit dem Radius r = ex0
abgebildet |
|
Die Gerade
|
y = y0 |
wird auf den Strahl Arg w = y0 abgebildet |
|
Der Streifen
|
y0 < y < y0+2p
|
wird umkehrbar eindeutig auf C\{0} abgebildet |
Geometrisch kann man diese Abbildungseigenschaften wiefolgt veranschaulichen:
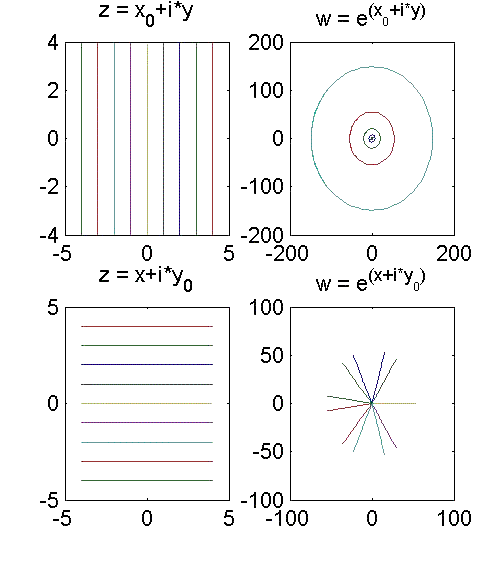 Diese Abbildungseigenschaften sind für die Funktion w = ez keineswegs symmetrisch, denn Kreise in der
z-Ebene
werden keinesfalls in Geraden in der w-Ebene transformiert (wie im Fall der Inversion),
wie man aus der nächsten Abb. sieht.
Diese Abbildungseigenschaften sind für die Funktion w = ez keineswegs symmetrisch, denn Kreise in der
z-Ebene
werden keinesfalls in Geraden in der w-Ebene transformiert (wie im Fall der Inversion),
wie man aus der nächsten Abb. sieht.
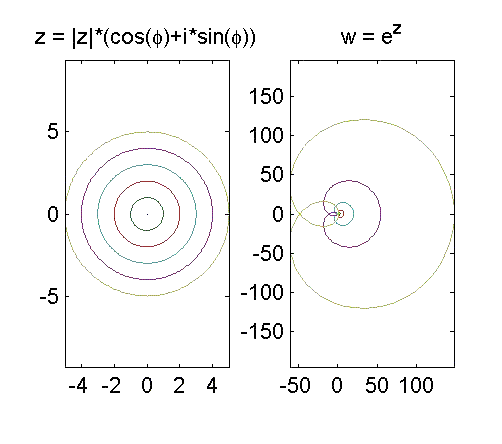 Aus der 2pi-Periodizität von w = ez folgt,
dass jeder Streifen der z-Ebene S = {x+iy; xÎÂ,
y0 < y < y0 +2pi}
umkehrbar eindeutig auf die gesamte z-Ebene ohne den Nullpunkt abgebildet werden
kann. Der Streifen F := {zÎC, -p
< Im z £ p}
heißt Fundamentalstreifen. Überlegen Sie, welche Bereiche des Fundamentalstreifens aus der z-Ebene durch
w = ez wohin in die
w-Ebene abgebildet werden.
Aus der 2pi-Periodizität von w = ez folgt,
dass jeder Streifen der z-Ebene S = {x+iy; xÎÂ,
y0 < y < y0 +2pi}
umkehrbar eindeutig auf die gesamte z-Ebene ohne den Nullpunkt abgebildet werden
kann. Der Streifen F := {zÎC, -p
< Im z £ p}
heißt Fundamentalstreifen. Überlegen Sie, welche Bereiche des Fundamentalstreifens aus der z-Ebene durch
w = ez wohin in die
w-Ebene abgebildet werden.
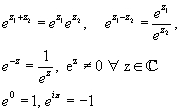 Eine Eigenschaft ist besonders wichtig, da sie die komplexe von der reellen Exponentialfunktion
unterscheidet - die Periodizität.
Für die komplexe Exponentialfunktion gilt folgende Eigenschaft:
Eine Eigenschaft ist besonders wichtig, da sie die komplexe von der reellen Exponentialfunktion
unterscheidet - die Periodizität.
Für die komplexe Exponentialfunktion gilt folgende Eigenschaft:
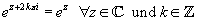 Dies ergibt sich aus folgendem Zusammenhang:
Dies ergibt sich aus folgendem Zusammenhang:
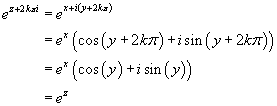 Die Periode der komplexen Exponentialfunktion beträgt 2pi. Diese Eigenschaft gibt es
im Reellen nicht.
Die Abbildung w = ez hat folgende Eigenschaften:
Die Periode der komplexen Exponentialfunktion beträgt 2pi. Diese Eigenschaft gibt es
im Reellen nicht.
Die Abbildung w = ez hat folgende Eigenschaften:
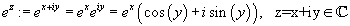 Daraus ergeben sich die Bestimmungen für Real-, Imginärteil, Betrag und Argument
Daraus ergeben sich die Bestimmungen für Real-, Imginärteil, Betrag und Argument
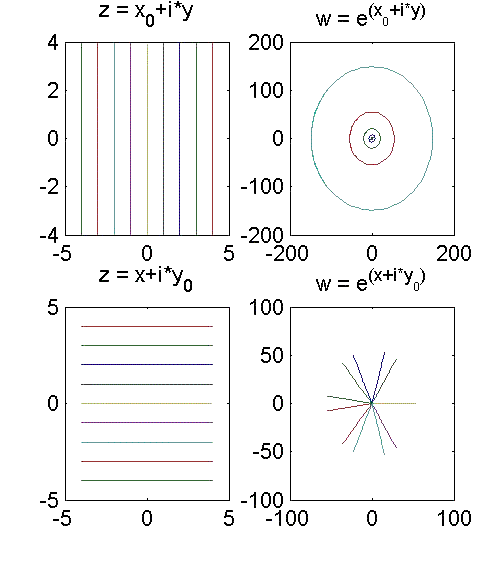 Diese Abbildungseigenschaften sind für die Funktion w = ez keineswegs symmetrisch, denn Kreise in der
z-Ebene
werden keinesfalls in Geraden in der w-Ebene transformiert (wie im Fall der Inversion),
wie man aus der nächsten Abb. sieht.
Diese Abbildungseigenschaften sind für die Funktion w = ez keineswegs symmetrisch, denn Kreise in der
z-Ebene
werden keinesfalls in Geraden in der w-Ebene transformiert (wie im Fall der Inversion),
wie man aus der nächsten Abb. sieht.
 Aus der 2pi-Periodizität von w = ez folgt,
dass jeder Streifen der z-Ebene S = {x+iy; xÎÂ,
y0 < y < y0 +2pi}
umkehrbar eindeutig auf die gesamte z-Ebene ohne den Nullpunkt abgebildet werden
kann. Der Streifen F := {zÎC, -p
< Im z £ p}
heißt Fundamentalstreifen. Überlegen Sie, welche Bereiche des Fundamentalstreifens aus der z-Ebene durch
w = ez wohin in die
w-Ebene abgebildet werden.
Aus der 2pi-Periodizität von w = ez folgt,
dass jeder Streifen der z-Ebene S = {x+iy; xÎÂ,
y0 < y < y0 +2pi}
umkehrbar eindeutig auf die gesamte z-Ebene ohne den Nullpunkt abgebildet werden
kann. Der Streifen F := {zÎC, -p
< Im z £ p}
heißt Fundamentalstreifen. Überlegen Sie, welche Bereiche des Fundamentalstreifens aus der z-Ebene durch
w = ez wohin in die
w-Ebene abgebildet werden.