|
2.2 Unter-, und Obersumme
|

  

|
Unter der Unter-, bzw. Obersumme versteht man in der Integralrechnung zwei unterschiedliche Näherungsverfahren um die Fläche zwischen der x-Achse und einem Graphen zu bestimmen.
Sei f(x) eine stetige Funktion. Durch eine Zerlegung des betrachteten Intervalls [a,b] in äquidistante [= gleich große] Teilintervalle (Rechtecke), erhält man eine Approximation der Fläche. Hierbei unterscheidet man zwischen der Untersumme bzw. der Obersumme.
U (Untersumme) steht dabei für die Summe der Rechtecksflächen unterhalb der Funktion.
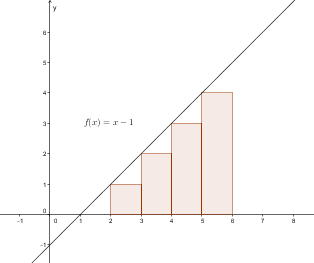
O (Obersumme) steht für die Summe der Rechtecksflächen oberhalb der Funktion.
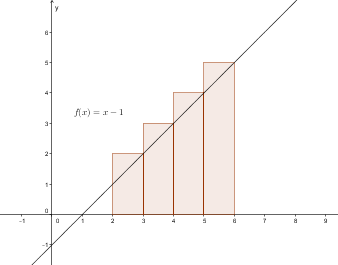
Die Anzahl der Rechtecke bezeichnet man als n.
Die Rechtecke der Untersumme haben den kleinsten Funktionswert f(xmin) im jeweiligen Teilintervall als Höhe. Aus diesem Grunde ist der Flächeninhalt aller Rechtecke der Untersumme insgesamt sicher kleiner als die Fläche unter der Funktion f. Die Rechtecke der Obersumme haben den größten Funktionswert f(xmax) im jeweiligen Teilintervall als Höhe. Der Flächeninhalt aller Rechtecke der Obersumme ist daher sicher größer als die gesuchte Fläche.
Je größer die Anzahl der Rechtecke wird, umso genauer werden Ober- und Untersumme und umso kleiner wird deren Differenz. Es gilt daher immer:
Untersumme U ≤ Fläche ≤ Obersumme O
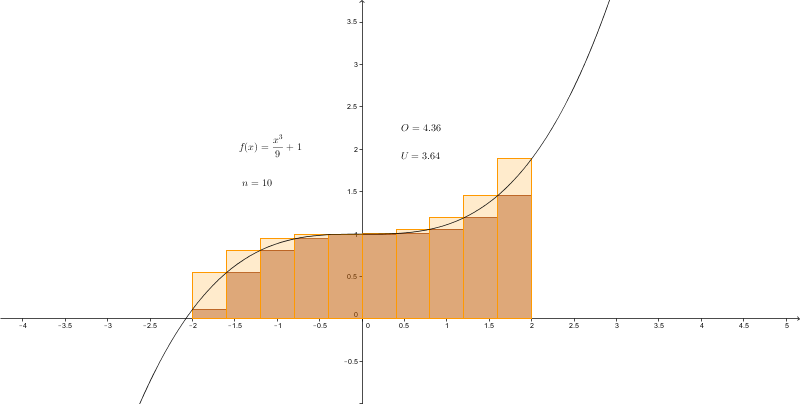
Diese Methode ist selbstverständlich sehr fehleranfällig, wenn man nur eine grobe Unterteilung des Intervalls vornimmt. Dieser Fehler wird kleiner, je feiner die Zerlegung des Intervalls ist bzw. je mehr Teilintervalle das Intervall besitzt.
Geht also die Anzahl der Rechtecke gegen Unendlich, so gehen die Ober- sowie auch die Untersumme gegen den Flächeninhalt.
Unter- und Obersumme können auch folgendermaßen angeschrieben werden:
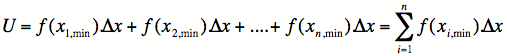

Bei dieser Überlegung steht Δx (Delta) für die Breite der Rechtecke, f(xi,min) für den niedrigsten Funktionswert im i-ten Teilntervall und f(xi,max) für den größten Funktionswert im i-ten Teilintervall. Ein weiteres Symbol wird für diese Formulierung verwendet, die man als Σ darstellt und Summe bedeutet.
Klicken Sie hier um ein Beispiel zur Berechnung der Unter-, bzw. Obersumme genauer durchzuarbeiten!
Eintrag in das Lerntagebuch
|
|
2.3 Aufgabenstellung zur Unter-, und Obersumme
|

 

|
Hier können Sie ihr Wissen über die Unter-, bzw. Obersumme anhand von Beispielen überprüfen.
Als Beilage finden Sie eine PDF-Datei, in der die einzelnen Aufgabenstellungen aufgelistet sind.
Übungsaufgaben
|
Lernpfadseite als User öffnen (Login)
Falls Sie noch kein registrierter User sind, können Sie sich einen neuen Zugang anlegen. Als registrierter User können Sie ein persönliches Lerntagebuch zu diesem Lernpfad anlegen.
|



