1. aÙ(rb) = r aÙb  und
2. aÙ(b + c) = aÙb + aÙc

aÙb = -bÙa

(ra)Ùb = r aÙb

(a + b)Ùc = aÙc + bÙc

Der Beweis von 1 ist einfach - dazu brauchen wir nur diese Skizze zu betrachten:

Wird b durch rb ersetzt, so ändert sich der Flächeninhalt des Parallelogramms um den Faktor |r|. Weiters ist rb parallel zu b, daher ändert sich die Richtung des Vektorprodukts nicht. Ist r negativ, so sorgt die Rechtsschraubenregel für das richtige Vorzeichen, womit 1 bewiesen ist.

Um 2 zu beweisen, verwenden wir eine sehr wirkungsvolle Argumentationsmethode: Sind die Vektoren a, b und c gegeben, so können wir unser dreidimensionales Koordinatensystem so in den Raum legen, dass es an die Problemstellung angepasst ist (und die nun notwendige Berechnung möglichst einfach wird):
Wir legen die z-Achse so, dass sie in Richtung des Vektors a weist.
Ein solches Koordinatensystem kann ebenso gut für Berechnungen verwendet werden wie jedes andere. In ihm hat der Vektor a die Komponenten
a  =  (0, 0, |a|).
Die beiden anderen Vektoren können beliebige Komponenten haben:
b  =  (b₁, b₂, b₃)
c  =  (c₁, c₂, c₃).
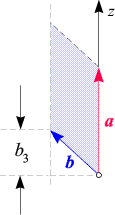
Als nächstes bemerken wir, dass das Vektorprodukt aÙb nicht von der z-Komponente b₃ von b abhängt. Der Grund dafür ist einfach: Ändern wir b₃, so ändert sich weder der Flächeninhalt des von a und b aufgespannten Parallelogramms,

Führen Sie die Maus in das Bild und wieder hinaus! Eine Änderung von b3 hat keinen Einfluss auf die Fläche des Parallelogramms.

noch die auf a und b normal stehende Richtung. Auch die Rechtsschraubenregel ist immer erfüllt, so dass für den vereinfachten Vektor
b'  =  (b₁, b₂, 0)
die Beziehung
aÙb = aÙb'
gilt. Der neue Vektor b' ist nichts anderes als die Projektion von b auf die xy-Ebene. Nun können wir die Komponenten von aÙb berechnen: Da das von a und b' aufgespante Parallelogramm ein Recheck mit Seitenlängen |a| und |b'| ist, ist der Betrag von aÙb gleich |a| |b'|. Weiters liegt aÙb in der xy-Ebene und steht normal auf b'. Aus der Rechtschraubenregel folgt, dass die Richtung von aÙb aus jener von b' durch eine Drehung (in der xy-Ebene) um 90° im Gegenuhrzeigersinn hervorgeht. Wenden wir diese Drehung auf (b₁, b₂, 0) an (vergleiche Formel (14) weiter oben in diesem Kapitel), erhalten wir (-b₂, b₁, 0). Der Betrag dieses Vektors ist |b'|. Muliplizieren wir ihn mit dem noch fehlenden Faktor |a|, so erhalten wir
aÙb  =  (-|a| b₂, |a| b₁, 0).
In völlig analoger Weise ergibt sich
aÙc  =  (-|a| c₂, |a| c₁, 0)
und
aÙ(b + c)  =  (-|a| (b₂ + c₂), |a| (b₁ + c₁), 0),
woraus unmittelbar
aÙ(b + c)  =  aÙb + aÙc
folgt. Damit ist auch 2 bewiesen.