Sinussatz im stumpfwinkeligen Dreieck:
Behauptung: Der Sinussatz
gilt auch in stumpfwinkeigen Dreiecken.
Beweis: Wir nehmen (ohne Beschränkung der Allgemeinheit) an, dass der
Winkel b stumpf (d.h. größer als 90°) ist:
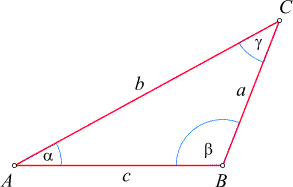
Wir fällen die Höhe auf die Seite c,
die nun außerhalb des Dreiecks liegt:
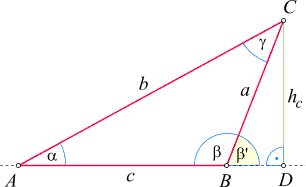
Ganz analog zum spitzwinkeligen Fall berechnen wir hc
auf zweierlei Arten:
- Im rechtwinkeligen Dreieck ADC (in dem die Seite b die Rolle der Hypotenuse spielt) erhalten wir
sin
a = hc/b,
daher
hc = bsina.
- Im rechtwinkeligen Dreieck BDC (in dem die Seite a die Rolle der Hypotenuse spielt) ergibt sich
sinb' = hc/a,
daher
hc = asinb',
wobei b' = 180° - b.
Nun gilt, wie im Kapitel Winkelfunktionen besprochen,
sin(180°
- b)
= sinb,
d.h. sinb'
= sinb.
Damit ergibt sich
| b sina =
a sinb, |
|
woraus unmittelbar
a
sina |
= |
b
sinb |
|
|
folgt. Die gleiche Argumentation kann mit der Höhe auf die Seite a
durchgespielt werden, was auf
c
sing |
= |
b
sinb |
|
|
führt und damit die Gültigkeit des kompletten Sinussatzes (5) erweist.