Spiegelung an einer beliebigen (durch den Ursprung verlaufenden) Geraden
In der Ebene wird die Spiegelung an einer beliebigen, durch den Ursprung verlaufenden Geraden $g$ durch
die Matrix
$S=u\,u^T-v\,v^T$
beschrieben,
wobei $u$ ein in Richtung der Geraden $g$ weisender Einheitsvektor und $v$ ein auf $u$ normal stehender
Einheitsvektor ist.
Anmerkung: In der Matrizensprache wir die Tatsache, dass $u$ und $v$ Einheitsvektoren sind, durch die
Beziehungen $$u^T u=v^T v=1$$
und die Tatsache, dass diese beiden Vektoren aufeinander normal stehen, durch
$$u^T v=0$$
zum Ausdruck gebracht.
Zum Beweis, dass die Matrix $S$ tatsächlich die gewünschte Spiegelung darstellt, zeigen wir zunächst, dass
sie $u$ und $v$ in ihre Spiegelbilder überführt:
$S\,u=\left(u\,u^T-v\,v^T\right)u=u\,\underbrace{u^T\,u}_{1}-v\,\underbrace{v^T\,u}_{0}=u$
und
$S\,v=\left(u\,u^T-v\,v^T\right)v=u\,\underbrace{u^T\,v}_{0}-v\,\underbrace{v^T\,v}_{1}=-v$.
Wird nun ein beliebiger Vektor in der Form
$$x=a\,u+b\,v$$
als Summe eines zu $g$ parallelen und eines zu $g$ normalen Vektors dargestellt ($a$ und $b$ sind
reelle Zahlen), so gilt
$S\,x=S\,(a\,u+b\,v)=a\,\underbrace{S\,u}_{\Large u}+b\,\underbrace{S\,v}_{\Large -v}=a\,u-b\,v$,
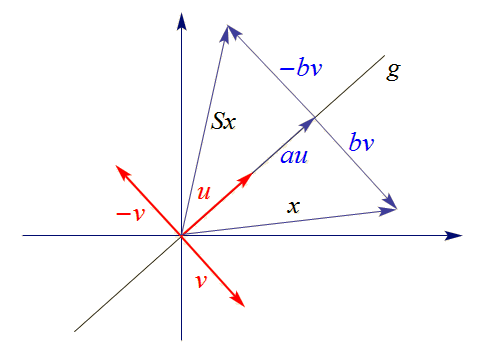
d.h. der Anteil parallel zu $g$ bleibt gleich, jener normal zu $g$ wird "umgedreht". Genau so
wirkt die gewünschte Spiegelung. Die folgende
Skizze veranschaulicht diesen Sachverhalt:
Beispiel: Mit $$u={1\over\sqrt{10}}\left(\begin{array}{c}1\\3\end{array}\right)$$ und
$$v={1\over\sqrt{10}}\left(\begin{array}{c}-3\\1\end{array}\right)$$
(überprüfen Sie selbst, dass $u$ und $v$ Einheitsvektoren sind, d.h. dass $u^Tu=v^Tv=1$ gilt,
und dass die beiden Vektoren aufeinander normal stehen, d.h. dass $u^Tv=0$ gilt!) ist
\begin{eqnarray}S&=&u\,u^T-v\,v^T=\\&=&{1\over 10}\left(\begin{array}{c}1\\3\end{array}\right)\left(\begin{array}{cc}1&3\end{array}\right)
-{1\over 10}\left(\begin{array}{c}-3\\1\end{array}\right)\left(\begin{array}{cc}-3&1\end{array}\right)=\\
&=&{1\over 5}\left(\begin{array}{cc}-4&3\\3&4\end{array}\right)\,{\sf\small.}
\end{eqnarray}

