Beispiele für Graphen: Stetigkeit
Der Graph einer stetigen Funktion ist eine zusammenhängende Kurve:
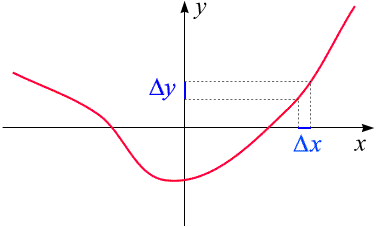
Das kann auch so ausgedrückt werden: Wird x um einen kleinen Wert
Dx
geändert, so ist die entsprechende Änderung Dy
des Funktionwerts ebenfalls klein.
Lässt man Dx
immer kleiner werden ("gegen Null streben"), so streben die entsprechenden
Dy
ebenfalls gegen Null.
Hingegen ist der Graph einer unstetigen Funktion keine zusammenhängende Kurve.
Diese hier besitzt eine Sprungstelle:
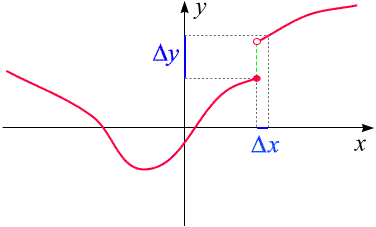
Beachten Sie: die gezeigte Funktion ist auch an der Sprungstelle definiert.
Der zugehörige Funktionswert ist durch den vollen roten Punkt
dargestellt.
Wird in diesem Beispiel x um einen kleinen Wert
Dx
geändert, so kann die entsprechende Änderung Dy
des Funktionwerts groß sein.
Strebt Dx
gegen Null (wobei der linke Punkt des blauen Dx-Intervalls
immer bei der Sprungstelle liegt), so wird sich
Dy
einer von Null verschiedenen Konstante (der grün strichliert
eingezeichneten vertikalen Größe der "Lücke"
= dem Abstand der Punkte und
) annähern,
also nicht gegen Null streben.