Schachbrettaufgaben
Mit einem Schachbrett kann man hervorragend spielen. Schach natürlich, aber nicht nur das. Auf dem Schachbrett ist für mathematische Spiele und Rätsel viel Platz.Aufgaben mit Schachbrettern sind leicht zu verstehen, schließlich kennt jeder das Schachbrett. Die Lösungen führen in verschiedene mathematische Gebiete.
1 Verschiedene Zählungen
1.1 Reiskörner
Der Erfinder des Schachbretts soll angeblich für seine Erfindung folgenden Lohn gefordert haben:Für das erste Feld 1 Reiskorn, für das zweite 2 und für jedes weitere Feld doppelt soviel Körner wie für das vorangehende Feld.
War das eine bescheidene Forderung? Lösung
[Quelle: www.mathekiste.de]
Wie viele Quadrate aus Gitterlinien können auf einem Schachbrett gezeichnet werden?
[Quelle: Mathematik online (Institut für Mathematik und ihre Didaktik, Uni Flensburg)]
Ein Dominostein sei genau so groß wie zwei Schachfelder, man kann das ganze Brett also mit 32 Stück zupflastern, und zwar auf viele, auch auf ausgesprochen
fantasiearme Arten.
Wie ist es aber mit 31 Dominosteinen, wenn zwei Felder übrig bleiben sollen, z.B. die linke obere Ecke und die rechte untere Ecke?
[Quelle: Aufgabenstellung als
Frage 123 bei
Norbert Treitz, Uni Duisburg]
Kann man 8 Damen so auf ein 8 x 8 Brett stellen, daß sie sich nicht gegenseitig bedrohen?
Über das Problem wird berichtet:
Es gibt genau 92 verschiedene Lösungen.
Das Problem der 8 Damen ist sehr bekannt und auch heute noch als Übungsaufgabe zur Programmierung beliebt.
Um mit einem Computerprogramme nach Lösungen zu suchen, gibt es verschiedene Verfahren.
Das einfachste nennt sich "Backtracking". Dabei wird Dame um Dame auf das Feld gesetzt, solange noch eine weitere Dame plaziert werden kann. Das Verfahren endet, wenn eine Lösung mit 8 Damen gefunden wurde, oder man nicht mehr weitersetzen kann. In diesem Fall nimmt
man einen Zug zurück (track back) und versucht eine Lösung über eine andere Plazierung früher gesetzter Damen zu finden.
Die Aufgabe dient vielfach als Testbeispiel, zur Veranschaulichung oder Überprüfung von Computer-Algorithmen. Beispielsweise für Neuronale Netze: Das 8-Damen-Problem
Dazu heißt es dort: "Die Energie eines Hopfieldnetzes sinkt mit jeden Schaltschritt kontinuierlich ab. Hierdurch eignet sich diese Art von Netzen zum Lösen von Optimierungsaufgaben. Als Beispiel wird hier das 8-Damen und das 8-Türme-Problem mit einem Hopfieldnetz gelöst."
Man versuche zu beweisen, daß man nicht mehr als acht Türme so auf einem Schachbrett plazieren kann, daß sie sich nicht gegenseitig bedrohen!
Hinweis: Ein Turm bedroht alle Felder derselben Zeile und derselben Spalte, eine Dame alle Felder derselben Zeile, Spalte und Diagonalen. Ein Läufer bedroht alle Felder derselben Diagonalen.
Ein König bedroht alle (maximal acht) direkt benachbarten Felder. Der Springer schließlich bedroht alle
von ihm aus im Rösselsprung erreichbaren Felder (,,Zwei vor/zurück, eins zur Seite``
oder ,,Eins vor/zurück, zwei zur Seite``).
[Quelle:
Aufgabenstellung
von Mathematischer Korrespondenzzirkel Göttingen]
"Nein" ist die Antwort.
Die Argumentation hat mit der Lösung der Dominoaufgabe nicht viel gemeinsam. Richtig ist, daß
es auch hier auf die schwarzen und weißen Felder ankommt. Aber das ist nicht genug.
Das andere wesentliche Argument ist, daß 8 eine gerade Zahl ist.
Um den Einfluß der geraden Anzahl Felder zu sehen, betrachte ich
ein Schachbrett mit nur 3x3 Feldern.
In einem 3x3 Schachbrett ist ein Mäuseweg ohne Feldwiederholung von links unten nach rechts oben möglich.
Es ist ja nicht verlangt,
daß die Maus nach jedem Stück Speck auch noch ein Stück Käse essen m u ß.
Es handelt sich hier nämlich nicht um das Domino-Stein-Problem, sondern
um die Frage nach einem Hamilton-Weg, also einer "Reise" von Start nach Ziel,
bei der jeder andere Ort der Karte genau einmal besucht wird.
Ich fasse die Felder des Schachbretts als Knoten eines Graphen auf. Zwei Felder sind
durch eine (ungerichtete) Kante verbunden, wenn sie mit einer Seite aneinander grenzen.
Für den Eingang links unten, füge ich eine weitere Ecke und Kante hinzu.
Für den Ausgang rechts oben, füge ich eine weitere Ecke und Kante hinzu.
Der Graph für ein 2x2 Problem (erweitert um Kanten zum Start und zum Ziel)
Ein notwendige Bedingung dafür, daß in einem Graphen G=(V,E)
ein Hamilton-Weg existiert, lautet:
V ist die Menge der Ecken (engl. vertices), E ist die Menge der Kangen (edges). G-S ist der Graph, der aus G entsteht, wenn man die Ecken aus S und mit ihnen alle Kanten an diesen Ecken entfernt. #S bezeichnet die Anzahl der Elemente in S, also die Anzahl der entfernten Ecken.
Im Falle eines geraden n betrachte das nxn Schachbrett und den entsprechenden Graphen
mit den beiden Zusatzecken und -kanten.
[Quelle für Aufgabenstellung: de.sci.mathematik]
In der Einleitung heißt es: "Es gibt manchmal Probleme, die so schwer sind, daß sie entweder nur Verrückten oder Genies einfallen konnten. Und dann gibt es auch wieder solche wie das Springerproblem.".
Auch dieses Problem gehört zu den Hamilton-Wege-Problemen.
[Quelle: Axel Conrad]
Zur Aufgabe mit Bildern.
[Quelle: Matheweb am Bundesgymnasium Babenbergerring, Wiener Neustadt]
Man bestimme diejenigen Werte von n, für welche das Spiel mit nur einem verbleibenden Spielstein beendet werden kann!
[Quelle: Aufgabenstellung von
Mathematik-Olympiaden e.V.]
[Aufgabenstellung früher unter http://www.mi.uni-erlangen.de/didaktik/aufgaben/ausgabe_001/algebraproblem.html (Mathematikdidaktik am Mathematischen Institut der Universität Erlangen-Nürnberg)]
Ich habe versucht die Vielfalt dieses Themas zu zeigen und das Material sinnvoll zu ordnen und zu kommentieren.
Dabei habe ich so gewissenhaft, wie es mir möglich war, die Quellen und Verweise angegeben.
Die Aufgaben sind teilweise schon Allgemeingut (Reiskörner), aber oft habe ich die Formulierung für eine Aufgabe von anderen übernommen. Lösungen habe ich hier nur wiedergegeben, wenn sie von mir stammen. Fremde Lösungen findet man als Verweise. Für einige Aufgaben gebe ich keine Lösungen an - versuche es selbst.
Sollte aber jemand der Meinung sein, daß ich seine Copyright verletze, oder daß die Urheberschaft nicht deutlich oder nicht richtig bezeichnet ist, dann bitte ich um eine Mail an Martin Wohlgemuth. Ich werde dann unverzüglich die erforderlichen Änderungen vornehmen.
Für Hinweise auf Fehler oder Tipps zur Vervollständigung dieser Arbeit wäre ich dankbar.
1.2 Gitterquadrate auf dem Schachbrett

2. Überdeckungen mit Dominosteinen
Eigentlich haben Dominosteine auf dem Schachbrett nichts zu suchen, aber trotzdem:

3. Aufstellung von Figuren
3.1 Damen
3.1.1 Normales Schachbrett
Die Königin ist die mächtigste Schachfigur. Sie kann in Reihen und Spalten ziehen. Zusätzlich kann sie sich auf den Diagonalen bewegen.
Wenn ja, wie viele Möglichkeiten gibt es?
"Dieses Problem tauchte zum ersten Mal 1848 in einer Schachzeitung auf, die von der Berliner Schachgesellschaft herausgegeben wurde. Sie stand auch in der "Illustrierten Zeitung" vom 1. Juni 1850, einer allgemeinen Zeitschrift unter der Rubrik Schach. Dadurch fand sie große Leserschaft.... Es gab aber nun einen Leser,
der alle Lösungen gefunden hatte und dieser Mann war von Geburt an blind."
Versuche mit dem Java-Applet bei ZERO selbst eine Lösung zu finden. Auf Wunsch gibt das Programm für jeden Zug eine Bewertung oder macht Vorschläge.
Wenn es eine Lösung gibt, dann findet das Verfahren sie. Allerdings wächst die Zeit
für größere Probleme exponentiell an. Das
Backtracking Java-Applet von Dr. Hans-Bernhard Meyer veranschaulicht das Backtracking-Verfahren am Beispiel der 8 Damen auch in dieser Hinsicht.
3.1.2 Allgemeines nxn Schachbrett
Wem 8 Damen nicht genügen, der kann es mit
n Damen auf einem nxn-Schachbrett versuchen (Otto Buchegger, Tübingen).
3.2 Türme
Man kann auf einem Schachbrett acht Türme so aufstellen, daß sie sich gegenseitig nicht bedrohen, zum Beispiel wie in folgendem Bild:

Außerdem finde man (mit Begründung!) für jede der Schachfiguren Dame, Läufer, König und Springer jeweils die maximale Anzahl N, für die man N derartige Figuren auf einem Schachbrett plazieren kann, ohne daß sie sich gegenseitig bedrohen.
4. Wege über das Schachbrett
4.1 Das hungrige Mäuslein
Ein hungriges Mäuslein sitzt in einem Schachbrett-Käfig, auf dem Feld links unten. Es kann von jedem Feld geradeaus ins Nachbarfeld links oder rechts, ober- oder unterhalb gelangen, aber nicht diagonal marschieren. Alle weißen Felder sind mit einem Käsestück bedeckt, die schwarzen mit einem Stück Speck.
Oben rechts ist der Ausgang. Kann das Mäuschen zum Ausgang gelangen und dabei alle Felder leerfressen, ohne ein zweites Mal ein leergefressenes Feld zu betreten?

o---o---o
| |
o---o---o
Und für 3x3 (erweitert um Kanten zum Start und zum Ziel)
o---o---o---o
| | |
o---o---o
| | |
o---o---o---o
Auf einem Hamilton-Weg müssen alle Ecken genau einmal durchlaufen werden. Ob
dagegen die Kanten alle durchlaufen werden, spielt keine Rolle. (Im allgemeinen gibt
es Kanten, die man für den Hamilton-Weg nicht benötigt.)
Das Traveling Salesman Problem (TSP) ist die bekannteste Formulierung einer Aufgabe, in der eine kürzeste Rundreise, also ein geschlossener Hamilton-Weg gesucht ist. Mehr über kürzeste Rundreisen in einem Artikel von Martin Grötschel und Manfred Padberg: Die optimierte Odyssee.
Für jede echte Teilmenge S der Ecken ist die Anzahl der Zusammenhangskomponenten
von G-S kleiner gleich #S+1.
Wenn nämlich in G ein Hamilton-Weg existiert, dann ist G zusammenhängend. Durch
Entfernen einer Ecke erhöht sich die Anzahl der Zusammenhangskomponenten höchstens
um 1 usw.
Wenn man in diesem Graphen alle Ecken, die den schwarzen Feldern des Schachbretts
entsprechen, entfernt, dann erhält man n²/2+2 Zusammenhangskomponenten.
Es wurden aber nur n²/2 Ecken entfernt. Darum kann es in diesen Graphen für gerades n
keinen "Mäuseweg" geben.
o---x---o
| |
o---x---o
x = entfernte Ecke
Für ungerade n kann man auf diese Art nichts erfahren.
x---o---x---o
| | |
o---x---o
| | |
o---x---o---x
Es werden [n²/2]+1 Ecken entfernt und die Anzahl der Zusammenhangskomponenten ist
danach [n²/2]+2.
Das notwendige Kriterium ist für ungerade n erfüllt.
Und in der Tat gibt es für ungerade n immer einen Mäuseweg. Ist ja leicht anzugeben.
4.2 Knight's Tour
Gegeben sei ein leeres Schachbrett. Gibt es eine Zugfolge, mit der der
Springer alle (schwarzen und weißen) Felder des Brettes genau einmal
besucht?

Eine ausführliche Arbeit über diese und naheliegende Fragen unter dem Titel Knight's Tour von Axel Conrad.
5. Weitere Aufgaben
5.1 Das zersägte Schachbrett
Peters kleiner Cousin war zu Besuch. Er war von dessen Laubsägewerkzeug so beeindruckt, daß er es gleich ausprobieren wollte. In einer unbewachten Stunde
machte er sich über Onkels Schachbrett her und zersägte es - unten seht ihr die Stücke ! Setzt die Teile wieder zusammen!
5.2 Durchgesägtes Schachbrett
Hier hat jemand ein (verallgemeinertes) Schachbrett mit 12 x 12 Feldern fast diagonal durchgesägt und dann wieder zusammengeklebt. Das Dreieck rechts oben sollte die Lücke links unten ausfüllen, aber trotzdem stimmt hier etwas nicht.
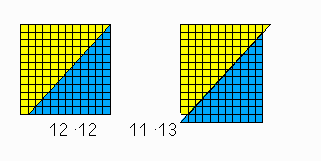
[Quelle: Aufgabenstellung als
Frage 13 bei
Norbert Treitz, Uni Duisburg]
5.3 Das schiefe Schachbrett
Die Felder auf diesem schiefen Schachbrett, bei dem jede Seite in 8 gleiche Abstände geteilt ist und bei dem alle Linien gerade sind, sind offensichtlich ungleich groß.
Sind wenigstens die hellen zusammen genau so groß wie die dunklen zusammen?

[Quelle: Aufgabenstellung als
Frage 46 bei
Norbert Treitz, Uni Duisburg]
5.4 Unendliches Schachbrett
Auf einem unendlichen Schachbrett wird folgendes Spiel gespielt: Zu Beginn sind n2 Spielsteine auf dem Schachbrett in einem (n×n)-Quadrat von benachbarten Feldern so angeordnet, daß auf jedem dieser Felder ein Spielstein liegt. Ein Zug in dem Spiel ist ein Sprung eines Spielsteines in horizontaler oder vertikaler Richtung über ein benachbartes belegtes Feld auf ein unmittelbar dahinter liegendes unbelegtes Feld. Der übersprungene Stein wird anschließend entfernt.
5.5 Anwendung eines unendlichen Schachbretts zur Lösung einer Algebra Aufgabe
Im Jahr 1926 wurde im Rahmen des "Eötvös Wettbewerbs" für Schüler in Ungarn die folgende Aufgabe* gestellt:
(I) Man beweise, wenn a und b gegebene Zahlen sind, dann besitzt das Gleichungssystem
Nach dem Wettbewerb wurden die Teilnehmer darauf aufmerksam gemacht, daß die Behauptung in Aufgabe (I) gleichwertig mit der Behauptung der folgenden Aufgabe (II) ist:
x + y + 2z + 2t = a
2x - 2y + z - t = b
eine Lösung für ganze Zahlen x, y, z und t.
(II) Ein Springer, der sich auf einem Feld O eines unendlichen Schachbretts befindet, kann jedes Feld des Schachbretts erreichen. (Ein unendliches Schachbrett
besteht aus quadratischen Feldern, die die ganze Ebene überdecken.)
1.Man zeige, daß die Behauptung in den Aufgaben (I) und (II) gleichwertig sind.
2.Man löse Aufgabe (II) und finde dadurch eine Lösung für Aufgabe (I).
6. Nachwort
Mit der Idee zu dieser Sammlung habe ich mich im Internet auf die Suche nach Schachbrettaufgaben gemacht.
Zur Illustration zeige ich einige Abbildungen von fremden Seiten. Ich bitte das als Einladung an Besucher zu verstehen, die "zitierte" Seite zu besuchen.
Martin Wohlgemuth für Matroids Matheplanet 23.9.2001 (Letzte Änderung 22.7.2002).

Mehr von Matroid [Das Prinzip der vollständigen Induktion] [Über Fraktale und mathematische Kunst]
[Volumenberechnung eines Ringes mit konstanter Höhe]
[Lösung von Extremwertaufgaben mit Differentialrechnung]
[Ein Problem aus der Stahlindustrie]
[Über die Anzahl von Sitzordnungen am runden Tisch]