Trigonometrische Funktionen am Einheitskreis

1 / 8

Welche Aussage stimmt nicht?
1. tan(π)=tan(2·π)
2. tan(π/4)=1
3. tan(x)=sin(x)/cos(x)
4. tan(π/2)=0
Welche Aussage über die Variable x, die wiefolgt definiert ist, stimmt?
x=tan(π/4)·sin(253°)
1. x = 1
2. x ist eine positive reelle Zahl
3. x = 0
4. x ist eine negative reelle Zahl
Für welchen Winkel γ mit 0 < γ < 360° gilt die folgende Aussage?
cos(γ) = 0.5
1. γ₁=60° γ₂=330°
2. γ₁=60° γ₂=120°
3. γ₁=60° γ₂=240°
4. γ₁=60° γ₂=300°
Kreuze die richtige(n) Aussage(n) an!
1. Sinus- und Cosinus sind 2·π-periodisch
2. Eine Funktion heißt "periodisch", wenn sich ihre Funktionswerte in regelmäßigen Abständen wiederholen.
3. Sinus, Cosinus und Tangens sind periodische Funktionen.
4. Sinus und Cosinus sind periodische Funktionen, der Tangens ist nicht periodisch.
5. Sinus, Cosinus und Tangens haben die selbe kleinste Periode.
In welchen Quadranten kann der Winkel α liegen, wenn folgendes gilt?
Sinus(α) = -0.345
1. Im 3.- und 4. Quadranten
2. Im 1.- und 2. Quadranten
3. Im 2.- und 4. Quadranten
4. Im 1.- und 3. Quadranten
Was stimmt in der nebenstehenden Figur nicht?
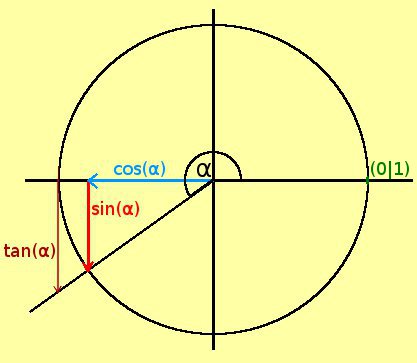
1. Nichts (die nebenstehende Figur ist korrekt)
2. Beim dargestellten Kreis, handelt es sich nicht um einen Einheitskreis.
3. sin(α) und cos(α) sind vertauscht
4. tan(α) ist falsch eingezeichnet
Welche Winkelfunktion(en) sind im 4. Quadranten positiv?
1. Cosinus und Tangens
2. Sinus
3. Cosinus
4. Keine (alle sind negativ)
Für welchen der angeführten Winkel β gilt die folgende Aussage?
sin(β) = -cos(β)
1. 45°
2. 135°
3. 3·π/4
4. π/2

Trigonometrische Funktionen am Einheitskreis

Quiz