1. Grenzwert:

Bei der Definition des Grenzwertes einer Funktion F( x,y ) muss man beachten, dass der Grenzwert der Funktion im Punkte P( ) nicht vom Weg abhängen darf, auf dem die Folge geordneter Paare ( ) gegen P strebt. Falls man das nicht beachtet, kann man Fälle konstruieren, bei denen eine Funktion in ein und demselben Punkt mehrere unterschiedliche Grenzwerte hat.

Beispiel:

F( x,y ) = 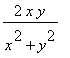 , P( ) = (0,0)

1. Weg: ,  , da 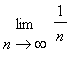 = 0 , kann man sagen ( )-->(0,0) und F( ) = 0 und  = 0

2. Weg: , , auch in diesem Fall gilt ( )-->(0,0), aber F( ) =  = 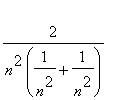1 und somit  = 1

Würde man also die Unabhägigkeit des Grenzwertes einer Funktion vom Weg, auf dem (x,y) gegen ( )  strebt, nicht fordern, hätten wir hier schon zwei Grenzwerte. Man sieht sehr schnell, dass man noch unendlich viel andere Werte durch Veränderung des Weges bekommt. Graphisch sieht die Funktion so aus:

>	F:=(x,y)->((2*x*y)/(x^2+y^2));

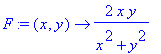
>	with(plots):

>	plot3d(F(x,y),x=-1..1,y=-1..1,orientation=[78,86],axes=FRAME,title="Graphik von ((2*x*y)/(x^2+y^2))");

>

Man sieht, dass in die Funktion in (0,0) eine Unregelmässigkeit hat. Um diese besser zu verstehen, gehen wir zu Polarkoordinaten über.

x = , y = . Man sieht F( x,y ) wird zu F( ) =  = 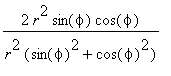, d.h. der Wert der Funktion hängt nur vom Winkel  ab, nicht vom Radius r. Mit anderen Worten, auf einem Strahl aus dem Ursprung sind die Funktionswerte konstant, sie ändern sich aber, wenn man zu einem anderen Strahl übergeht.

Man definiert deshalb den Grenzwert einer zweiwertigen Funktion im Punkte  so:

Gegeben sei eine zweiwertige Funktion F(x,y) in einer Umgebung U von . Es sei P( ) eine beliebige  Folge von geordneten Paaren, die gegen den Punkt  strebt. Wenn der Grenzwert der Funktion F(x,y) für jede dieser Folgen existiert und denselben Wert c hat, dann sagt man, dass F(x,y) in P( ) einen Grenzwert besitzt und schreibt  = c.

2. Stetigkeit

In Anlehnung an die Definition der Stetigkeit für Funktionen einer Variablen wird die Stetigkeit für Funktionen mehrerer Variabler bestimmt:

Eine zweiwertige Funktion F(x,y) heißt stetig im Punkte  = ( ), wenn der Grenzwert  im Punkte  gleich dem Funktionswert im Punkte ist.  Alle Überlegungen zu Grenzwert und Stetigkeit lassen sich auch auf den  erweitern.

Unser obiges Beispiel zeigt, dass diese Funktion nicht stetig ist in (0,0). Es lässt sich auch keine stetige Ergänzung vornehmen.

3. Theoreme:

1. Es sei F(x,y) stetig in  und F( ) < 0 oder > 0. Dann existiert eine Umgebung U von , so dass F(P) > 0 oder < 0 für alle Punkte P aus U.

2. Wenn F und G zwei Funktionen sind, die in einem Punkte  stetig sind, dann sich auch die arithmetischen Verknüpfungen dieser Funktionen in dem genannten Punkte stetig.

3. F(x,y) sei auf einer  Menge M erklärt, in M stetig und [M sei beschränkt (d.h. für alle Elemente x aus M existiert eine Zahl K mit  < K) und abgeschlossen (alle Randpunkte gehören zur Menge)] = (M ist kompakt). Dann besitzt F(x,y) in M ein absolutes Maximum und Minimum.

4. Es sei F(x,y) auf M stetig und es existiert ein Punkt ( ) in M mit F( ) > 0 und eine zweiter Punkt ( ) mit F( ) < 0, Dann existiert ein Punkt

( ) mit F( ) = 0.