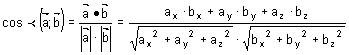auf
den Vektor 
mit dem Betrag von
Das
Skalarprodukt zweier VektorenAndreas
Pester Fachhochschule Techikum
Kärnten, Villach
pester@cti.ac.at
Zusammenfassung: In
diesem Abschnitt wird der Begriff des Skalarproduktes zweier Vektoren erklärt
Stichworte: Definition | Eigenschaften des Skalarprodukts
Das Skalarprodukt zweier Vektoren ist die Multiplikation der Projektion des Vektors auf
den Vektor mit dem Betrag von
Das Skalarprodukt zweier Vektoren ergibt einen skalare Größe und ist definiert durch:
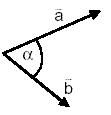
Dabei ist a der Winkel zwischen den
beiden Vektoren
und .
Ein Beispiel dafür ist:
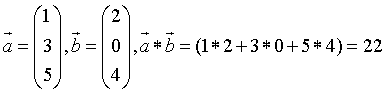
Wie man sieht ist das Ergebnis eine Zahl (22), kein Vektor.
Für das Skalarprodukt (sofern es überhaupt berechenbar ist) gilt:
1)  |
Kommutativgesetz |
2) |
Distributivgesetz |
3)  |
Assoziativgesetz |
und stehen
genau dann senkrecht aufeinander, sind also orthogonal, wenn ihr
Skalarprodukt verschwindet: 
.
