und
.LösungenAndreas
Pester Fachhochschule Techikum
Kärnten, Villach
pester@cti.ac.at
Zusammenfassung: In
diesem Abschnitt wird der Begriff Länge (Betrag) eines Vektors erklärt
Stichworte: Definition | Gleichheit von Vektoren
Lösung
a) Vektor.
b) Kein Vektor.
c) Kein Vektor.
Lösung
(a) un (b) sind beide Rechtssysteme.
Lösung 1
Vektorgrafik.
Lösung 2
Pixelgrafik.
Lösung 1
Der Vektor hat Länge und eine Richtung.
Lösung 2
Gleich sind und
.
Parallel sind
,
und -
.
Invers parallel zu
und ist
.
Ungleich sind
und
,
und
,
ist
.
Lösung 1
= 47,17
Lösung 2
Der Betrag eines Vektors hat keine Richtung, der Betrag ist eine skalare Größe.
Lösung 1
Lösung 2
x = -8.
Lösung 3
x = -2,497 y = -6,860 z = 0
Lösung 1
Zuerst bilden wir den Gegenvektor y' des Vektors y:
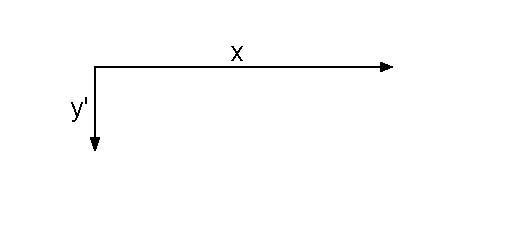
Nun addieren wir x und y', und erhalten die
Differenz x-y:
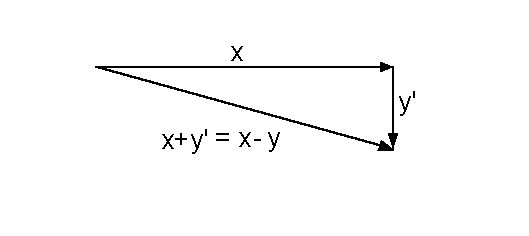
Die Differenz x-y multiplizieren wir
nun mit 0.5,
d.h. wir halbieren die Länge des
Vektors x-y:
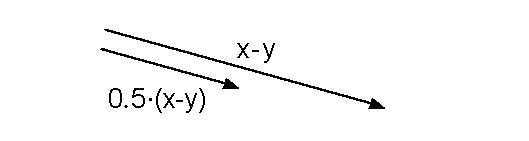
Lösung 1
Lösung 2
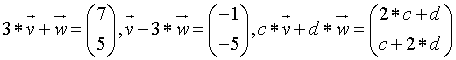
Lösung 1
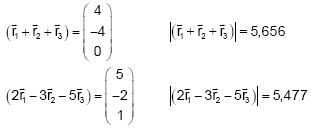
Lösung 2
Lösung 1
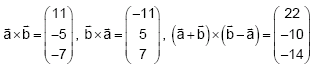
Lösung 2
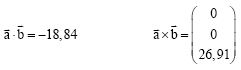
Lösung 3
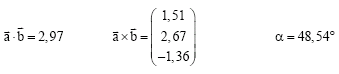
Lösung:
