Gauß'sche Zahlenebene
Andreas Pester
Fachhochschule Technikum Kärnten
pester@cti.ac.at
Zusammenfassung: Hier wird die geometrische Darstellung komplexer Zahlen behandelt. Vorraussetzung dafür sind die
Kenntnis der Polarkoordinaten und des Kartesischen Koordinatensystems.
Komplexe Zahlen - Inhaltsübersicht
Stichworte:
Gauß'sche Zahlenebene |
Dreiecksungleichung |
Unleichung 1 |
Ungleichung 2 |
Ungleichung 3 |
Denksport 1 |
Argument |
Polarkoordinaten |
trigonometrische Form einer komplexen Zahl |
Denksport 2
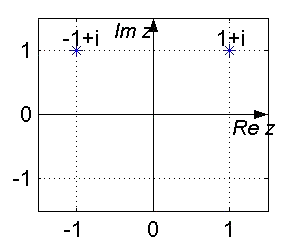
Den Realteil x = Re
z und den Imaginärteil
y = Im z einer komplexen Zahl kann man
auch eineindeutig als geordnetes Paar (x,y) schreiben und als Punkt auf der Ebene
Â2 interpretieren. Diese Ebene nennt man die
Gauß'sche Zahlenebene oder komplexe Zahlenebene. Punkte der Form (x,0) =
x (reelle Zahl)
liegen auf der x-Achse,
der sogenannten reellen Achse Re z, Punkte der Form
(0,y) = y·i
(rein imaginäre Zahl) liegen auf der y-Achse, der imaginären
Achse Im z.
 Der Betrag |z| =
Ö(x2+y2)
ist dann nichts anderes als der Abstand des Punktes (x,y) vom Ursprung (0,0).
Daraus folgen die zwei Ungleichungen:
|x| = |Re z| £
|z|
Der Betrag |z| =
Ö(x2+y2)
ist dann nichts anderes als der Abstand des Punktes (x,y) vom Ursprung (0,0).
Daraus folgen die zwei Ungleichungen:
|x| = |Re z| £
|z|
|y| = |Im z| £
|z|
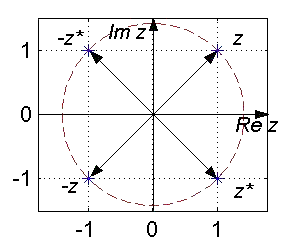
Die Zahlen z, z*, -z und
-z* haben alle den gleichen Betrag,
d.h. den gleichen Abstand vom Ursprung. Mit anderen Worten, sie
liegen alle auf einem Kreis mit dem Mittelpunkt im Ursprung und dem Radius |
z|
.
Für mathematisch Interessierte: Die komplexe Zahlenebene ist ein metrischer Raum. Der Euklidische Abstand
d zwischen zwei Punkten
z1 = (
x1
,y1) und
z2 =
(x2,
y2) auf dieser Ebene kann durch
d = |
z1 -
z2| dargestellt werden.
Eine Folge von komplexen Zahlen z
n = xn + yn·i für n = 1,2,... konvergiert dann gegen eine Zahl
z*, wenn
|zn -
z*|
®
0 für n ® ¥
Nach einem wohlbekannten Theorem für die Konvergenz eine Punktfolge im Euklidischen Raum gilt
dass d.u.n.d., wenn
xn ®
x* und
yn
® y* für
n ® ¥
Eine komplexe Zahl z = x+y·i kann auch als Ortsvektor vom Punkte (0,0) zum Punkte
(x,y) interpretiert werden.
Somit wird die Addition von zwei komplexen Zahlen z = x+y·i und
w = u+v·i zu
z + w = (x+u) + (y+v)·i
zur bekannten Vektoraddition
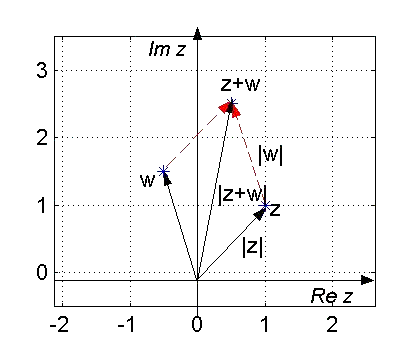
Die Dreiecksungleichung sieht dann wie folgt aus:
|z + w| £ |z| + |w|
Aus z = (z - w) + w folgt dann
|z| £
|z - w| + |w|
|z - w| ³ |z| - |w|
Genauso lässt sich zeigen
|z - w| = |w - z| ³
|w| - |z|
ergo
|z - w| ³
||z| - |w||
Kurze Denkaufgaben:
- Man zeige, dass alle komplexen Zahlen mit Im z < 0 in der unteren Halbebene (ausschließlich der x-Achse) liegen
- Man zeige, dass alle komplexen Zahlen mit Re z £ 0 in der linken
Halbebene
(einschließlich der y-Achse) liegen
- Man überlege, welche komplexen Zahlen die Gleichung |z| / |z*| = 1 erfüllen und wo diese Zahlen auf der Ebene liegen
- Man überlege, wo die Zahlen Im z > Re z auf der komplexen Ebene liegen
- Man zeige, dass alle komplexen Zahlen z, die die Ungleichung |z
- z0| £ R erfüllen, innerhalb
eines Kreises mit dem Radius R und dem Mittelpunkt z0 liegen
Als Argument einer komplexen Zahl bezeichnet man den Winkel f, den die als Vektor interpretierte komplexe Zahl z mit der
positiven x-Achse einschließt und schreibt Arg z = f.
Damit gilt 0 £ Arg z £ 2p.
Unter Nutzung der bekannten Formeln für die Polarkoordinaten kann man leicht zeigen, dass:
Re z = |z|·cos(f)
Im z = |z|·sin(f)
z = |z|·(cos(f)+
i·sin(f))
z* = |z|·(cos(-f)+
i·sin(-f))
Unter Nutzung der Eigenschaften der sin und cos Funktionen bekommt man leicht
z* = |z|·(cos(f)-
i·sin(f))
Die Darstellung einer komplexen Zahl in (4) nennt man die trigonometrische Form einer komplexen Zahl.
In dieser Form lassen sich komplexe Zahlen besonders gut multiplizieren und dividieren und die Ergebnisse in der komplexen
Zahlenebene interpretieren. Man schau dazu unter
Trigonometrische Form komplexer Zahlen nach.
Zum Abschluss noch einmal
Kurze Denkaufgaben:
- Wo in der Ebene liegen die komplexen Zahlen, für die gilt 0 < Arg z <
p/4
-
Wie ist der Zusammenhang zwischen Arg z und Arg z* ?
-
Wo liegen die komplexen Zahlen in der Ebene, für gilt |z| = Arg z
 Der Betrag |z| =
Ö(x2+y2)
ist dann nichts anderes als der Abstand des Punktes (x,y) vom Ursprung (0,0).
Daraus folgen die zwei Ungleichungen:
|x| = |Re z| £
|z|
Der Betrag |z| =
Ö(x2+y2)
ist dann nichts anderes als der Abstand des Punktes (x,y) vom Ursprung (0,0).
Daraus folgen die zwei Ungleichungen:
|x| = |Re z| £
|z|
