Definitionslücke und hebbare Singularität

Größere Schriftzeichen

Definitionslücke und hebbare Singularität:

Um zu verstehen, was es mit diesen Begriffen auf sich hat, diskutieren wir es anhand eines Beispiels:

Eine Funktion sei durch den Term

x (x² - 1)

x - 1

(1)

gegeben. Da er für x = 1 nicht definiert ist (die Division 0/0 macht keinen Sinn), liegt die Stelle x = 1 zunächst nicht im Definitionsbereich. Unsere Funktionsdefinition lautet daher:

f (x) =

x (x² - 1)

x - 1

(2)

mit dem Definitionsbereich

A = R \ {1}

(3)

(die Menge der reellen Zahlen ohne die 1). Wird der Ausdruck x²-1 im Zähler als (x+1)(x-1) geschrieben, so wird klar, dass man den Funktionsterm für jedes x Î A (d.h. für jedes x ¹ 1) kürzen kann. Daher kann (2) durch

f (x) = x (x + 1)

(4)

ersetzt werden. Der Definitionsbereich ist nach wie vor durch (3) gegeben. Der Graph unserer Funktion f sieht so aus:

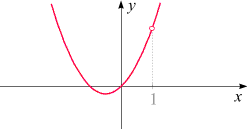
An der Stelle x = 1 klafft eine Lücke. Hier liegt offensichtlich ein Schönheitsfehler vor. Beachten Sie, dass das ursprüngliche Problem mit dem Term (1) fast verschwunden ist. Es hat sich gewissermaßen "herausgekürzt".

Da der Ausdruck (4), wenn er für alle x Î R zugelassen wird, eine überall stetige Funktion definiert, kann die Lücke "stetig geschlossen" werden. Es muss lediglich der Funktionswert an der Stelle x = 1 nachträglich als 2 definiert werden. Damit wird unsere Funktion stetig auf ganz R ausgedehnt.

In kurzen Worten zusammengefasst: Die Lücke wurde beseitigt, indem der Funktionsterm ordentlich gekürzt wurde. Daher sprechen wir von einer Definitionslücke oder von einer hebbaren Singularität.

Nachbemerkung 1: Die oben vorgeführte Methode funktioniert für rationale Funktionen, d.h. Quotienten zweier Polynome, versagt aber in komplizierteren Fällen. Wir werden später im Kapitel Anwendungen der Differentialrechnung eine allgemeinere Methode besprechen, die uns etwa erlauben wird, zu erkennen, dass die Definitionslücke in

f (x) =

sin x

(5)

an der Stelle x = 0 durch die Definition f (0) = 1 stetig behoben werden kann.

Nachbemerkung 2: Natürlich definiert nicht jeder Term, auch wenn er ordentlich gekürzt ist, eine stetige Funktion. Betrachten wir etwa statt (1) den Term

x (x² + 1)

x - 1

(6)

so liegt an der Stelle x = 1 eine "echte" Singularität (eine Polstelle) vor. Das erkennen wir daran, dass sein Betrag unbeschränkt anwächst, wenn sich x der Zahl 1 annähert. Für (1) ist das natürlich nicht der Fall.