Das Prinzip der vollständigen Induktion

"Seht Euch doch diesen Mathematiker an", sagt der Logiker, "er bemerkt, dass die ersten neunundneunzig Zahlen kleiner als hundert sind und schließt daraus auf Grund von etwas, das er Induktion nennt, dass alle Zahlen kleiner als hundert sind."

"Ein Physiker glaubt", sagt der Mathematiker, "das 60 durch alle Zahlen teilbar ist. Er bemerkt, dass 60 durch 1, 2, 3, 4, 5 und 6 teilbar ist. Er untersucht noch ein paar Fälle wie 10, 20 und 30, die, wie er sagt, aufs Geratewohl herausgegriffen sind. Da 60 auch durch diese teilbar ist, betrachtet er seine Vermutung als hinreichend durch den experimentellen Befund bestätigt."

"Ja, aber seht Euch doch die Ingenieure an", sagt der Physiker. "Ein Ingenieur hatte den Verdacht, dass alle ungeraden Zahlen Primzahlen sind. Jedenfalls, so argumentiert er, kann 1 als Primzahl betrachtet werden. Dann kommen 3, 5 und 7, alle zweifellos Primzahlen. Dann kommt 9; ein peinlicher Fall, wir scheinen hier keine Primzahl zu haben. Aber 11 und 13 sind unbestreitbar Primzahlen. 'Auf die 9 zurückkommend', sagt er, 'schließe ich, dass 9 ein Fehler im Experiment sein muss.'"

Es liegt nur allzu sehr auf der Hand, dass Induktion zum Irrtum führen kann. Um so bemerkenswerter ist es, da die Irrtumswahrscheinlichkeiten so überwältigend erscheinen, dass Induktion manchmal zur Wahrheit führt.
[Mathematik-Folklore]

Die vollständige Induktion ist eine der 3 grundlegenden mathematischen Beweistechniken - neben 'direkt' und 'indirekt durch Widerspruch'. Um eine Beweistechnik als Mittel der korrekten logischen Argumentation zu akzeptieren, muss man diese Technik verstanden haben. Das Prinzip der vollständigen Induktion ist immerhin schon so komplex, dass es Gegenstand von Witzen sein kann.

Themenüberblick

1. Wer hat die vollständige Induktion erfunden?
2. Ist Induktion nur etwas für Folgen und Reihen?
3. Wie funktioniert die vollständige Induktion?
   1. Zusammenfassung Induktionsverfahren
4. Kann man sich auf die vollständige Induktion verlassen?.
5. Kann man denn wirklich den Induktionsschluss unendlich oft anwenden?.
6. Was ist schwer an der vollständigen Induktion?
7. Kann man denn Induktion immer anwenden?
   1. Peano-Axiome
8. Induktion kann man nicht anwenden, wenn ...
9. Anwendungen der vollständigen Induktion
   1. Geometrie
   2. Mengenlehre
   3. Binomialkoeffizienten
   4. Geometrisches und Arithmetisches Mittel
   5. Summenformeln
   6. Abschätzungen
   7. Teilbarkeit
   8. Zahlentheorie
   9. Rekursiv definierte Folgen
   10. Eindeutigkeitsbeweis
   11. Differentialrechnung
10. Schluss

1. Wer hat die vollständige Induktion erfunden?

   Induktives Denken, also das Schließen vom Besonderen auf das Allgemeine, gibt es solange Menschen denken. Die Frage ist also, seit wann die vollständige Induktion methodisch so ausformuliert und handhabbar war, dass man von einer erlaubten und zuverlässigen Beweistechnik sprechen kann. Philosophen, Wissenschaftler, Mathematiker haben schon im Altertum induktive Beweise gegeben. Die strenge mathematische Induktion ist das nicht in jedem Fall gewesen und es gab jahrhundertelange Dispute.

   In einem Beitrag der TU Freiberg steht

   Der erste Mathematiker, der einen formalen Beweis durch vollständige Induktion angab, war der italienische Geistliche Franciscus Maurolicus (16.9.1494 - 21./22.7.1575). Er war Abt von Messina und wurde als größter Geometer des 16. Jahrhunderts angesehen. In seinem 1575 veröffentlichten Buch Arithmetik benutzte Maurolicus die vollständige Induktion unter anderem dazu, für jede positive ganze Zahl n die Gültigkeit von

   1 + 3 + 5 + ... + (2n-1)=n*n

   zu beweisen. Die Induktionsbeweise von Maurolicus waren in einem knappen Stil geschrieben, dem man nur schwer folgen kann. Eine bessere Darstellung dieser Methode wurde von dem französischen Mathematiker Blaise Pascal (1623 - 1662) angegeben. In seinem 1662 erschienen Buch Traite du Triangle Arithmetique bewies er eine Formel über die Summe von Binomialkoeffizienten mittels vollständiger Induktion. Er benutzte diese Formel dann um das heute nach ihm benannte Pascalsche Dreieck zu entwickeln.

   Obwohl die Methode der vollständigen Induktion also bereits 1575 bekannt war, wurde der Name dafür erst 1838 erstmalig gebraucht. In jenem Jahr veröffentlichte Augustus de Morgan (1806 - 1871), einer der Begründer der Mengenlehre, den Artikel Induction (Mathematics) in der Londoner Zeitschrift "Penny Cyclopedia". Am Ende dieses Artikels benutzte er den Namen für die vollständige Induktion erstmals im heute üblichen Sinn. Jedoch fand diese Bezeichnung erst in unserem Jahrhundert ihre weite Verbreitung.
   [Zitat aus einem Internet-Artilel "Vollständige Induktion" von Prof. Dr. rer. nat. Udo Hebisch]

   Übrigens das Gegenteil von Induktion ist die Deduktion, bei der man vom Allgemeinen auf das Einzelne schließt. Beispiel: Alle Menschen haben einen Kopf. Peter ist ein Mensch. Folgerung: Peter hat einen Kopf. Aber darum soll es weiter nicht gehen.



2. Ist Induktion nur etwas für Folgen und Reihen?

   Nein, aber bei diesen Schulthemen, die üblicherweise in der 11. Klasse behandelt werden, wird die vollständige Induktion eingeführt. Bis dahin bestand keine Notwendigkeit dazu. Anwendung der vollständigen Induktion findet man in allen mathematischen Gebieten, von Mengenlehre bis Geometrie, von Diffenrentialrechnung bis Zahlentheorie. Sogar der Beweis des großen Fermatschen Satzes (Wiles) verwendet die vollständige Induktion (neben vielen anderen Argumenten).

   Ich werde unten vielfältige Beispiele für Beweise mit vollständiger Induktion geben.

3. Wie funktioniert die vollständige Induktion?

Für eine gegebene Behauptung zeigt man, dass die Behauptung für ein oder einige kleine n gilt (Induktionsanfang). Ausgehend von dieser wahren Voraussetzung zeigt man, dass die Behauptung für das nächste n (also n+1) sich aus der Gültigkeit der Behauptung für ein oder alle kleineren Zahlen n herleiten lässt.
Die hierbei verwendete Schlussweise ist so vorzunehmen, dass sie "übertragbar" oder "wiederverwendbar" ist.
Wenn eine Behauptung z.B. für n=1 ist richtig ist, dann hat man damit den Induktionsanfang. Der Induktionsanfang ist der feste Punkt, an den alles folgende anknüpft. Ohne Induktionsanfang ist auch ein noch so schöner Induktionsschluss nichts wert. Man kann aus einer Aussageform A vielleicht die Aussageform B folgern. Aber um zu wissen, ob B deswegen wahr ist oder nicht, muss man wissen, ob A wahr ist oder nicht.
Das ist nicht schwer zu verstehen. Nehmen wir die Aussagen A: [5 ist durch 2 teilbar] und B: [7 ist durch 2 teilbar]. Natürlich ist 5 nicht durch 2 teilbar, aber aus der Aussage [5 ist durch 2 teilbar] folgert man logisch korrekt, dass auch 7 durch 2 teilbar ist. Die Schlussweise ist auf jeden Fall korrekt, nur die Voraussetzung war eben nicht gegeben.

Wenn also der Induktionsanfang abgesichert ist, dann weiß man, dass die Behauptung für alle n kleinergleich einem bestimmten n₀ gilt (das ist oft nur eine einzige natürliche Zahl, meistens die 1).
Diese Formulierung mit n₀ nennt man dann die Induktionsvoraussetzung.

Nun kommt der Induktionsschritt. Formal lautet der:
Aus der Gültigkeit der Behauptung für n≤n₀ folgt die Gültigkeit der Behauptung für n≤n₀+1 (die Induktionsbehauptung).

Wenn man das zeigen kann, was hat man dann davon?
Wenn die Behauptung für n₀=1 gilt, dann gilt sie auch für n₀=2.
Wenn die Behauptung für n₀=2 gilt, dann gilt sie auch für n₀=3.
Wenn die Behauptung für n₀=3 gilt, dann gilt sie auch für n₀=4.
usw.
Den Induktionsschritt von n->n+1 kann man beliebig oft (in Gedanken) anwenden. Die Schlussweise ist immer die gleiche.
Folglich gilt die Behauptung für alle n ∈ IN.

Ich habe jetzt zur Verdeutlichung immer n₀ geschrieben, weil man die Induktionsvoraussetzung nur für eine oder einige natürliche Zahlen geprüft hat und voraussetzen darf. Mehr war im Induktionsanfang ja nicht nachgewiesen worden. In der Praxis schreibt man eigentlich immer n statt n₀ und weiß dennoch, was gemeint ist.

Zusammenfassung Induktionsverfahren

Die Folge von Induktionsanfang, Induktionsvoraussetzung, Induktionsbehauptung und Induktionsschritt nennt man vollständige Induktion.
1. Prüfe den Induktionsanfang: A(0).
2. Formuliere die Induktionsvoraussetzung: A(n).
3. Formuliere die Induktionsbehauptung: A(n+1).
4. Beweise den Induktionsschritt: A(n) → A(n+1).

Vielleicht sollte ich zur Klarheit noch die Begriffe Aussage und Aussageform erklären. Eine Aussage ist eine überprüfbare Eigenschaft irgendwelcher konkreten Dinge. Beispiele: [Menschen haben einen Kopf] oder [Primzahlen sind durch 2 teilbar]. Eine Aussage kann wahr oder falsch sein, aber sie ist auf jeden Fall überprüfbar bzw. entscheidbar. Eine Aussageform dagegen ist eine Aussage, die eine Variable enthält, z.B. [n ist durch 2 teilbar]. Bei der vollständigen Induktion ist A(0) eine Aussage und A(n) eine Aussageform. Auch [A(n)→A(n+1)] ist eine Aussageform. Dagegen ist das, was man eigentlich mit vollständiger Induktion beweisen will, nämlich [Für alle natürlichen Zahlen n gilt A(n)] eine Aussage und keine Aussageform, denn dies ist eine Aussage über alle natürlichen Zahlen, deren Wahrheitsgehalt nicht von der Wahl eines bestimmten n abhängt. Die Aussage ist nämlich falsch, wenn sie für eine einzige natürliche Zahl n₀ nicht gilt, egal welches. Ein Beispiel: Die Aussage [alle natürlichen Zahlen sind kleiner als 100] ist falsch. Die Aussageform [die natürliche Zahl n ist kleiner als 100] dagegen ist wahr für n<100 und falsch für n>99.



4. Kann man sich auf die vollständige Induktion verlassen?

   Ja, wenn man die Beweistechnik richtig anwendet. Man darf nicht schludern. Wenn man mit vermeintlich vollständiger Induktion glaubt offensichtlichen Unsinn beweisen zu können, dann hat man einen Fehler gemacht. Solche Fehler kommen vor, berechtigen aber nicht zu Zweifeln an der Methode. Ebensowenig zweifelt man an den Regeln für Termumformungen, nur weil man sich beim Ausklammern oder Zusammenfassen oder den Minuszeichen vertun kann.
   Gelegentlich sind falsche "Induktionsschlüsse" gerade dazu geeignet, die letzten Unsicherheiten bzgl. der Beherrschung der Methode aufzudecken und zu beseitigen.

   Falsches Beispiel 1:

   Behauptung: In einen Koffer passen beliebig viele Paar Socken.
   Beweis durch vollständige Induktion: Induktionsanfang: n=1: Ein Paar passt in einen leeren Koffer, Ok!

   Induktionsschluss von n auf n+1: In einem Koffer seien n Paar Socken. Ein Paar passt immer noch hinein, das ist eine allgemeingültige Erfahrung. Also sind nun n+1 Paar in dem Koffer. Ok!

   Dieses Beispiel (gefunden bei www.mathekiste.de) ist ein Witz und gehört zur Mathematik-Folklore. Der echte Fehler in diesem "Beweis" liegt darin, dass man Erfahrung nur mit geringen Anzahlen von Socken hat.

   Falsches Beispiel 2:

   Behauptung: Wenn sich unter n Tieren ein Elefant befindet, dann sind alle diese Tiere Elefanten.
   Beweis durch vollständige Induktion:
   Induktionsanfang: n=1 : Wenn von einem Tier eines ein Elefant ist, dann sind alle diese Tiere Elefanten.
   Induktionsvoraussetzung: Die Behauptung sei richtig für alle natürlichen Zahlen kleiner oder gleich n.
   Induktionsschluss: Sei unter n+1 Tieren eines ein Elefant. Wir stellen die Tiere so in eine Reihe, dass sich dieser Elefant unter den ersten n Tieren befindet. Nach Induktionsannahme sind dann alle diese ersten n Tiere Elefanten. Damit befindet sich aber auch unter den letzten n Tieren ein Elefant, womit diese auch alle Elefanten sein müssen. Also sind alle n+1 Tiere Elefanten. ?????

   Was daran falsch ist?
   Im Fall n+1=2 kann man den Elefanten zwar so stellen, dass er bei den ersten n=1 Tieren steht. Folglich sind alle Tiere unter den ersten n=1 Tieren Elefanten. Aber deshalb befinden sich unter den "letzten" n Tieren nicht notwendig Elefanten.
   
   Der Induktionsschluss funktioniert nur für n>1, denn nur dann können aus einem Elefanten zwei (oder mehr) werden und ist damit auch ein Elefant unter den letzten n Tieren.
   Die Induktionsvoraussetzung war aber gezeigt für n=1.
   Man müsste also zunächst zeigen, dass von zwei Tieren, von denen eines ein Elefant ist, auch das andere ein Elefant ist. Aber das wird schwer.
   Der eigentliche Fehler des "Beweises" liegt darin, dass (n+1)/2 nicht immer größer als 1 ist. Wenn wir uns n+1 Dinge in einer Reihe vorstellen, dann sehen wir vor unserem inneren Auge eine lange Reihe, mit 10 oder 20 oder 1000 Dingen (Tieren). Aber eine Reihe von Tieren kann auch aus 2 Tieren bestehen. Dafür gilt der vermeintliche Induktionsschluss nicht.



5. Kann man denn wirklich den Induktionsschluss unendlich oft anwenden?

   Das dauert doch unendlich lange, und noch niemand hat das jemals bis zum Ende durchführen können.
   Guter Einwand. Man muss das auch nicht tun. Die Formulierung "für alle n" scheint das nahezulegen, aber es nicht so. Wenn eine Behauptung durch vollständige Induktion bewiesen ist, dann zeigt der Beweis, wie aus vorausgesetztem A(n) die Gültigkeit für A(n+1), also der gleichen Aussageform für die nächste natürliche Zahl, folgt. In die Behauptung, die wir gerne für alle n als richtig einsehen möchten, wird niemals ∞ eingesetzt. Wir verwenden die Behauptung immer für ein festes aber beliebiges n. Wenn wir eine Summenformel Σ_k=1ⁿ k = n*(n+1)/2 verwenden, dann z.B. für n=1000. Den Induktionsschluss aus dem Beweis der Summenformel kann man theoretisch 1000-mal durchführen, Wenn aber die Summe der Zahlen bis n=1.000.000 gefragt ist, dann machen wir den Induktionsschluss 1.000.000-mal. Das dauerte zwar lange, ist aber in endlicher Zeit zu schaffen (und wenn nicht von einem Menschen, dann von 100 Menschen oder mit Computern).
   Tatsächlich wird niemand jemals den Induktionsschritt eine Million mal anwenden. Der Induktionsschluss zeigt ja, wie das jeweils zu machen ist. Und das reicht. Die Zeit können wir uns sparen.
   Aber es ging ja hier auch um die Frage nach der unendlichen Wiederholbarkeit des Induktionsschlusses. Antwort: Der Induktionsschluss muss nicht unendlich oft wiederholt werden. Die durch vollständige Induktion gewonnenen Formeln und Ergebnisse gelten für feste aber beliebige natürliche Zahlen n.

6. Was ist schwer an der vollständigen Induktion?

   Die vollständige Induktion ist ein konstruktives Beweisverfahren. Der Induktionsschritt zeigt wie man im allgemeinen die Gültigkeit einer Behauptung aus einfachen Anfängen heraus auf alle möglichen Objekte (Zahlen) ausweitet.
   Konstruktive Beweise erfordern konstruktive Argumente. Solche muss man erst einmal finden. Konstruktiv kann ein Argument ja nur sein, wenn es in Bezug auf die Aufgabenstellung wirklich etwas aussagt. Im oben angeführten Sockenbeispiel war das Argument [die Erfahrung sagt, dass immer noch ein Paar Socken mehr in den Koffer passt] nicht konstruktiv. Ein konstruktives Argument sagt genau wo, die Lücke für das weitere Paar Socken sein wird.
   Man kann induktive Beweise nur führen, wenn man die durch die Ausgangssituation gegebenen Fakten gut analysiert und eine Idee entwickelt, die dem Problem genau angemessen ist.

   Die Durchführung des Induktionsschritts erfordert zudem handwerkliche mathematische Fähigkeiten. Gerade bei Induktionsbeweisen muss man die Regeln der Termumformungen und die Handhabung von Summenzeichen und Variablenindizes beherrschen. Nur dann kann man die richtige Idee auch wirklich verifizieren.



7. Kann man denn Induktion immer anwenden?

   Was heißt "immer"? Man kann Induktion nur anwenden, wenn die Behauptung irgendwelche Objekte (Zahlen, Geraden, Teilmengen, ...) behandelt und wenn zwischen den Objekten und den natürlichen Zahlen eine Bijektion (eine eineindeutige Abbildung) möglich ist.
   Ich werde später Beispiele für Anwendung der vollst. Induktion auf andere Objektmengen als die natürliche Zahlen geben. Um die vollst. Induktion anwenden zu können, genügt, dass die Objektmenge die Peano-Axiome erfüllt.
   

   Die natürlichen Zahlen standen ganz am Anfang unseres Aufbaus des Zahlensystems. Wir haben so getan, als seien sie unproblematisch und jedermann vom Abzählen und vom Anordnen her wohlbekannt. Das war auch in der geschichtlichen Entwicklung der Mathematik so. Während die irrationalen und die negativen Zahlen den Gegenstand von langwierigen Auseinandersetzungen bildeten, kümmerte man sich um die natürlichen Zahlen nur wenig. Gegen Ende des 19. Jahrhundert änderte sich dies. Den Mathematikern war es gelungen alle anderen Zahlenarten auf die natürlichen zurückzuführen. Damit stellte sich die Frage "Was ist eigentlich eine natürliche Zahl?" Eine Antwort hierauf gab der italienische Mathematiker Giuseppe Peano (1858-1932) im Jahre 1889. Peano nannte fünf Eigenschaften, die die Menge der natürlichen Zahlen N kennzeichnen:

   Die Axiome der natürlichen Zahlen nach Peano:

   1. 1 ist eine natürliche Zahl.
   2. Zu jeder Zahl n gibt es eine eindeutig bestimmte natürliche Zahl n*, genannt der Nachfolger von n.
   3. 1 ist nicht der Nachfolger irgendeiner natürlichen Zahl.
      
   4. Zwei natürliche Zahlen n und m, deren Nachfolger gleich sind (d.h. m* = n*), sind selbst gleich (d.h. m = n).
   5. Es sei T eine Teilmenge der natürlichen Zahlen mit folgenden Eigenschaften:
      1. 1 gehört zu T;
      2. gehört n zu T, dann ist auch der Nachfolger n* von n ein Element von T.
      Dann stimmt T mit N überein.

   Man nennt diese Eigenschaften heute die Peano-Axiome. Mit dem Begriff "Axiom" bezeichnet man Annahmen, die man als wahr voraussetzt. Für die Zwecke der Mathematik genügt es, die Menge der natürlichen Zahlen als dasjenige Gebilde zu betrachten, das diese fünf Eigenschaften besitzt.
   Das letzte, sehr komplex wirkende Axiom wird "Axiom der vollständigen Induktion" genannt.

   

8. Induktion kann man nicht anwenden, wenn ...

   Man kann also Aussagen über reelle Zahlen niemals mit vollständiger Induktion beweisen, denn es gibt keine Bijektion zwischen N und R (siehe Cantors Diagonalbeweis).

   Oftmals ist man auch versucht, die Induktion immer für möglich zu halten, wenn nur ein n in der Behauptung vorkommt. Wenn man etwas beweisen will oder muss, dann ist die Suche nach der richtigen Beweismethode erforderlich. Die Möglichkeit der Verwendung der vollst. Induktion gehört dazu. Man muss aber auch lernen, wann die vollständige Induktion nicht geeignet ist. Beispiel: Die Aussage: [Die Folge a(n) = 1/n ist immer positiv.] kann man nicht mit vollständiger Induktion beweisen. Wie sollte man aus A(n): [1/n > 0] denn folgern, dass A(n+1): [1/(n+1) > 0] ist? Gut, beide Aussageformen sind wahr, aber man kann A(n+1) nicht aus A(n) folgern. Man muss hier andere Argumente verwenden. Nicht aus jeder wahren Voraussetzung kann man jede andere wahre Behauptung folgern.

9. Anwendungen der vollständigen Induktion

   Für mich stammen die schönsten Beispiele für vollständige Induktionen aus dem Bereich der Geometrie. Man hat weniger mit mathematischem Handwerkszeug zu kämpfen und kann sich auf die Suche nach der (konstruktiven) Idee begeben, ohne schon an der sonst oft formalen Formulierung der Behauptung zu scheitern.

   1. Geometrie

      1. Aufgabe: Zeige, dass die Zahl d(n) der Diagonalen in einem ebenen, konvexen n-Eck durch die Formel

         d(n) = n/2 * (n-3)

         berechnet werden kann! Für welche n gilt die Formel?

         Lösung:
         Idee: vollst. Induktion über die Anzahl der Ecken.
         Induktionsanfang für ein Dreieck. Ein Dreieck hat keine Diagonalen, also d(3) = 0 = 3/2 * (3 - 3). Für n=3 ist die Behauptung richtig.
         Induktionsschritt: Stelle Dir ein konvexes n-Eck vor (z.B. ein Fünfeck). In dieses zeichne eine Diagonale von einem beliebigen Eckpunkt zu einem "übernächsten" Eckpunkt, also so, dass ein Dreieck und ein (n-1)-Eck entsteht.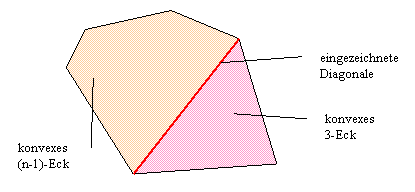

         Konvexes, ebenes n-Eck, durch eine Diagonale zerlegt in ein (n-1)-Eck und ein 3-Eck

         Das Dreieck hat keine und das (n-1)-Eck hat d(n-1) Diagonalen (Induktionsvoraussetzung).
         Außerdem muss man noch die Diagonalen von der Ecke des Dreiecks, die nicht eine Ecke des (n-1)-Ecks ist, zu allen Ecken des (n-1)-Ecks, die nicht Eckpunkt des Dreiecks sind, zählen - und nicht zu vergessen die eine Diagonale, mit der das Dreieck abgeteilt wurde.
         Folgt: d(n) = d(n-1) + (n-3) + 1
           = (n-1)/2 * ((n-1)-3) + (n-3) + 1
           = (n-1)*(n-4)/2 + n -2
           = (n²-5n+4)/2 + n -2
           = (n²-3n)/2
           = (n * (n-3)) / 2
         Fertig.

         Einige Bemerkungen:

         • Der Induktionsanfang wurde für n=3 gemacht. Für kleinere n kann man den Induktionsschluss nicht durchführen, das geht erst ab einem (3+1)-Eck. Ein Polygon mit weniger als 4 Ecken erlaubt nicht das Einzeichnen einer Diagonale von einer Ecke zu einer "übernächsten" Ecke. Im Dreieck ist ja jede andere Ecke benachbart.
         • Als Induktionsschritt wurde [A(n-1)→A(n)] gezeigt. Das ist erlaubt, man muss aber angeben, für welche n dieser Schritt gilt. Der Induktionsschritt gilt für alle n≥4. Es ist dasselbe, ob man für n≥3 [A(n)→A(n+1)] oder für n≥4 eben [A(n-1)→A(n)] zeigt. Warum der Induktionsschritt nicht von n auf n+1 vorgeführt wurde ...? Ach, das sind die kleinen Unwichtigkeiten, mit denen die Anfänger verwirrt werden.
      2. Behauptung: Durch n Geraden (in allg. Lage) wird die Ebene in (n²+n+2)/2 Teile zerlegt. (Anleitung: jede weitere Gerade zerlegt eine ganz best. Anzahl der schon vorhandenen Gebiete in 2 Teile.)

         Zunächst ist festzustellen, dass ein "höchstens" fehlt. Durch n Geraden wird die Ebene höchstens in ... Teile zerlegt. Die Geraden könnten ja parallel oder identisch sein.

         Induktionsanfang: n=1. Eine Gerade teilt die Ebene in 2 Gebiete und (1²+1+2)/2 ist gleich 2.

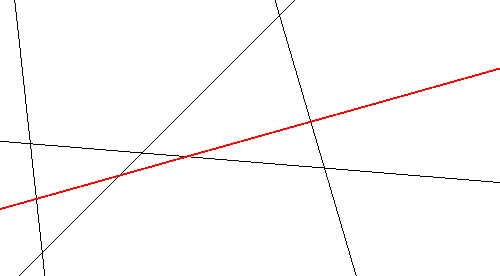
         Die (n+1)-te Gerade teilt maximal n+1 Gebiete

         
         Wie kann man den Induktionsschluss machen?
         Die (n+1)-te Gerade kann höchstens n Geraden schneiden. Immer wenn die neue Gerade eine vorhandene Gerade schneidet, dann tritt sie in ein neues Gebiet der Ebene ein. Die Anzahl der Gebiete, die von der neuen Geraden geteilt werden ist (höchstens) n+1, denn das erste Gebiet wird ja schon geteilt, bevor die neue Gerade die erste vorhandene Gerade schneidet. Und "höchstens" deshalb, weil ja vorkommen kann, dass zwei (oder mehr) Geraden zugleich geschnitten werden.
         Die Anzahl der neuen Gebiete ist also für n+1 höchstens = (n² + n + 2) / 2 + ( n + 1 ).
         Man kann dann zeigen, dass dies gleich ((n+1)² + (n+1) + 2) / 2 ist.

      3. Anzahl de Rechtecke in einem quadratischen Gitter. Induktion über die Summe der Zeilen und Spalten.
         

   2. Mengenlehre

      1. Behauptung: Sei M eine beliebige Menge und m=|M| die Anzahl der Elemente von M. Zeige, dass |P(M)|=2^m.

         Lösung: die Potenzmenge P(M) ist die Menge aller Teilmengen von M. Die Frage ist also, wieviele verschiedene Teilmengen man aus m Elementen bilden kann. Um das zu zählen gibt es verschiedene Möglichkeiten, ja nachdem, was man verwenden darf. Was man immer anwenden kann, ist vollständuge Induktion.
         A) Wenn M={}, also |M|=0, dann ist P(M)={{}}, denn nur die leere Menge ist Teilmenge der leeren Menge. Also |P(M)|=1=2⁰.
         B) Sei nun |M|=n+1. Sei x ein bestimmtes Element aus M. Bilden wir nun alle Teilmengen.
         
         Wir können die Teilmengen aufteilen in
         a) die Teilmengen, die x nicht enthalten,
         b) die Teilmengen, die x enthalten.
         
         Nach Induktionsvoraussetzung wissen wir, das die Anzahl der Teilmengen bei a) = 2ⁿ ist, denn es handelt sich ja um alle Teilmengen einer Menge mit n Elementen.
         In allen Teilmengen aus b) können wir das Element x entfernen. Dann ist die Anzahl dieser Mengen also auch = 2ⁿ, denn es handelt sich auch hier um alle Teilmengen einer Menge mit n Elementen.
         Addiere nun die Anzahlen für a) und b)
         2ⁿ + 2ⁿ = 2ⁿ⁺¹.
         Fertig.

   

   3. Binomialkoeffizienten

   1. Beweise ∑ⁿ _k=0 (^a+k_k) = (^a+n+1_n)
      
      Beweis mit Induktion:
      n=0: (^a+0₀) = (^a+0+1₀). Stimmt, denn beide Binomialkoeffizienten sind gleich 1.
      Induktionsschritt:
      Was ist zu zeigen:
      Unter der Voraussetzung, dass die Beziehung für n schon bewiesen ist, muss man zeigen:
      ∑ⁿ⁺¹ _k=0 (^a+k_k) = (^a+(n+1)+1_n+1)
      Also immer da wo n stand, muss jetzt n+1 stehen.
      
      Zum Beweis:
      ∑ⁿ⁺¹ _k=0 (^a+k_k)
      = ∑ⁿ _k=0 (^a+k_k) + (^a+n+1_n+1)
      = (^a+n+1_n) + (^a+n+1_n+1)
      = (^a+(n+1)+1_n+1)
      Fertig.
      Dabei habe ich die Summe mit n+1 Summanden erstmal aufgeteilt in n Summanden und einen. Für die Summe bis n kann man die Induktionsvoraussetzung anwenden.
      Schließlich gibt es noch eine Beziehung zwischen Binomialkoeffizienten, die es sich zu merken lohnt:
      (ⁿ_k-1)+(ⁿ_k) = (ⁿ⁺¹_k)
      [Diese Formel kann man auch wieder mit vollst. Induktion beweisen.]
      Damit habe ich dann zusammengefasst und erhalte das gesuchte Ergebnis.
   2. Beweise: Es sei x ∈ R. Man zeige für alle n ∈ IN, mit 0 eingeschlossen, gilt:
      
      (1+x)ⁿ=∑ⁿ _v=0(ⁿ_v) * x^v
      

      Auch das geht mit Induktion.
      Für n=0 steht da (1+x)⁰ = (⁰₀)*x⁰ und das ist richig.
      Für n=1: 1+x = (¹₀)*x⁰ + (¹₁)*x¹ auch richtig.
      Nun der Induktionsschritt:
      (1+x)ⁿ⁺¹ = (1+x)ⁿ * (1+x)
      = (1+x) * ∑ⁿ _i=0 (ⁿ_i)*xⁱ
      = 1* ∑ⁿ _i=0 (ⁿ_i)*xⁱ + x* ∑ⁿ _i=0 (ⁿ_i)*xⁱ
      = ∑ⁿ _i=0 (ⁿ_i)*xⁱ + ∑ⁿ _i=0 (ⁿ_i)*xⁱ⁺¹
      jetzt verschiebe ich den Index in der zweiten Summe.
      = ∑ⁿ _i=0 (ⁿ_i)*xⁱ + ∑ⁿ⁺¹ _i=1 (ⁿ_i-1)*xⁱ
      In den beiden Summen kommen die Potenzen x¹ bis xⁿ vor. Aber x⁰ ist nur in der ersten Summe und xⁿ⁺¹ nur in der zweiten Summe. Ich zerlege die Summen dementsprechend.
      = 1 + ∑ⁿ _i=1 (ⁿ_i)*xⁱ + ∑ⁿ _i=1 (ⁿ_i-1)*xⁱ + xⁿ⁺¹
      Und dann kann ich die beiden Summen zusameenfassen:
      = 1 + ∑ⁿ _i=1 [(ⁿ_i) + (ⁿ_i-1) ]*xⁱ + xⁿ⁺¹
      Nun gilt für die Binomialkoeffizienten die folgende Beziehung: (ⁿ_i) + (ⁿ_i-1) = (ⁿ⁺¹_i)
      Das eingesetzt ergibt:
      = 1 + ∑ⁿ _i=1 (ⁿ⁺¹_i)*xⁱ + xⁿ⁺¹
      und dann
      = ∑ⁿ⁺¹ _i=0 (ⁿ⁺¹_i)*xⁱ

   3. Beweis des Binomischen Lehrsatzes
      Beweise:
      (a+b)ⁿ = ∑ⁿ _i=0 (ⁿ_i) aⁱb^n-i
      Vollständige Induktion.
      n=0 => 1 = 1 stimmt!
      Induktionsschritt:
      (a+b)ⁿ⁺¹ = [ ∑ⁿ _i=0 (ⁿ_i) aⁱb^n-i ]*(a+b)
      unter Verwendung der Induktionsvoraussetung (für n).
      = a*∑ⁿ _i=0 (ⁿ_i) aⁱb^n-i + b* ∑ⁿ _i=0 (ⁿ_i) aⁱb^n-i
      = ∑ⁿ _i=0 (ⁿ_i) aⁱ⁺¹b^n-i + ∑ⁿ _i=0 (ⁿ_i) aⁱb^n-i+1
      = aⁿ⁺¹ + ∑^n-1 _i=0 n!/(i!*(n-i)!) aⁱ⁺¹b^n-i + bⁿ⁺¹ + ∑ⁿ _i=1 n!/(i!*(n-i)!) aⁱb^n-i+1
      
      Was passiert denn hier eigentlich?
      Um besser durchzublicken, schreibe ich die Formeln für n=3:
      (a+b)³ = [ a³ + 3a²b¹ + 3a¹b² + b³]*(a+b)
      = a *[ a³ + 3a²b¹ + 3a¹b² + b³] + b*[ a³ + 3a³b¹ + 3a¹b² + b³]
      = a⁴ + 3a³b¹ + 3a²b² + a¹b³ + a³a¹ + 3a²b² + 3a¹b³ + b⁴
      Die gemischten Potenzen kommen je zweimal vor, die Potenzen "hoch 4" je einmal. Ich ordne um:
      = a⁴ + (3+1)*a³b¹ + (3+3)*a²b² + (1+3)*a¹b³ + b⁴
      Aha, der Koeffizient vor a³b¹ ist die Summe von zwei anderen Binomialkoeffizienten. Und zwar (ⁿ_k-1)+(ⁿ_k) und das ist (ⁿ⁺¹_k).
      Und da haben wir die Formel für n=4.

      Entschuldigung, dass ich es dabei belasse. Bei der vorigen Aufgabe mit (1+x)ⁿ war ich noch ausführlich. Hier ist es doch genau dasselbe.

   

   4. Geometrisches und Arithmetisches Mittel

   1. Wie kann man denn am besten beweisen, dass das geometrische Mittel kleiner gleich dem arithmetischen Mittel ist? Induktion habe ich schon ausprobiert, aber... Seien a₁, ... ,a_n positive reelle Zahlen.
      Dann gilt: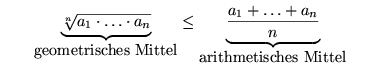
      

      Wir beweisen zuerst folgenden

      Hilfssatz: Gilt für reelle Zahlen b₁, ... ,b_n:
      ∏_k=1ⁿ b_k = 1, so ist ∑_k=1ⁿ b_k ≥ n
      Gleichheit gilt genau dann, wenn b₁=b₂=...=b_n.

      Beweis des Hilfssatzes mit vollständiger Induktion über n.
      Für n=1 gilt die Behauptung.
      Betrachte nun die Zahlen b₁,...,b_n,b_n+1.
      Wenn alle b_i gleich sind und ∏_k=1ⁿ b_k = 1, dann folgt, dass alle b_i=1,
      und es ist klar, dass ∑_k=1ⁿ b_k = n+1.
      Falls aber nicht alle b_i=1 sind,
      dann ist o.B.d.A. b₁ < 1 < b₂ weil ∏_k=1ⁿ b_k = 1.
      Aus b₁ < 1 < b₂ folgt, dass (1 - b₁)*(b₂ - 1) > 0.
      Ausmultipliziert ist das: b₁ + b₂ > 1 + b₁*b₂.

      Aus der Induktionsvoraussetzung folgt für die n Zahlen

      b₁*b₂, b₃, ... ,b_n, b_n+1:

      b₁*b₂ + ∑_k=3ⁿ⁺¹ b_k ≥ n.

      Insgesamt erhält man:
      .
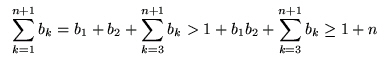      qed.

      Zurück zum Beweis der Behauptung über geometrisches und arithmetisches Mittel
      Wenn a₁ = a₂ = ... = a_n, dann ist die Behauptung trivial, und die Ungleichung gilt mit Gleichheit.

      Nehmen wir also an, dass die a_i nicht alle gleich sind.
      Sei G := .
      Betrachte b_i := a_i / G.

      Nach Konstruktion ist ∏_k=1ⁿ b_k = 1.
      Da nicht alle b_i gleich sind, folgt aus dem Hilfssatz: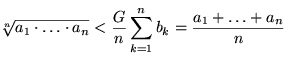
      
      QED.

   

   5. Summenformeln

   1. Vollständige Induktion ist wie Treppenlaufen lernen. Erst einmal muss man wissen, dass man überhaupt auf die erste Stufe klettern kann. Dann muss man den Weg finden, wie man von einer Stufe auf die nächste kommt. Und dann kommt man ja von der ersten auf die zweite, von der zweiten auf die dritte, etc.
      Wenn die erste Stufe nicht klappt, dann haut natürlich das ganze nicht hin.
      
      Summenformel für Zahlen von 1 bis n.
      Behauptung: 1+2+3+...+n = n*(n+1)/2
      
      Beweis mit Vollständiger Induktion:
      1. Induktionsanfang: n=1. 1 = 1*(1+1)/2 = 1 Passt.
      
      2. Induktionsvoraussetzung: Für alle n ≤ k gilt die Behauptung. Insbesondere also 1+2+...+k=k*(k+1)/2 ⇠ Das nennen wir jetzt abgekürzt "(IV)".
      
      3. Induktionsschritt. Man betrachtet, ob jetzt aus der Induktionsvoraussetzung schon folgt, dass auch für n = k+1 die Behauptung gelten muss. Also:
      1+2+3+...+k+(k+1) = (1+2+3+4+...+k) + (k+1)
      Jetzt setzen wir für den ersten Teil (IV) ein:
      = k*(k+1)/2 + k+1 = (k²+k)/2 + (2k+2)/2 = (k²+3k+2)/2 =
      (Faktorisieren)
      =(k+1)(k+2)/2 = (k+1)*((k+1)+1)/2
      
      Genau das sollte ja nach Behauptung herauskommen. Die Behauptung ist also bewiesen, denn... für n=1 wissen wir, was los ist. Daraus folgt n=2. Daraus für n=3, usw.
      Ich finde den Vergleich mit der Treppe gut.
   2. Beweise folgenden Satz: 1+4+9+....+n² = n*(n+1)*(2n+1)/6
      Für n=1, ist ∑ⁿ _k=1 n² = 1. ok.
      Nun ∑ⁿ⁺¹ _k=1 n² = ∑ⁿ _k=1 n² + (n+1)² = n * (n+1) * (2n+1)/6 + (n+1)²
      Um das zu zeigen, muss man mit Hilfe der Induktionsvoraussetzung die Terme der Induktionsbehauptung ausmultiplizieren und zusammenfassen, bis man das gewünschte Ergebnis (die Behauptung) vor sich stehen hat.
      
      Durch geschicktes Umformen kommt man schließlich auf (n+1) * (n+2) * (2(n+1)+1)/6.
      Oder man zeigt, dass gilt:
      n*(n+1)*(2n+1)/6 + (n+1)² - (n+1) * (n+2) * (2(n+1)+1)/6 = 0
      Kräftig ausmultiplizieren, dann sieht man's.
      Bemerkung: Ich habe ∑ⁿ⁺¹ _k=1 n² zuerst so geschrieben: ∑ⁿ _k=1 n² + (n+1)².
      Das habe ich gemacht, weil ich dann auf die Summe bis n die Induktionsvoraussetzung (für kleinere Zahlen als n+1) anwenden kann. Denn für kleinere Zahlen als n+1 gilt die Behauptung, nämlich:
      ∑ⁿ _k=1 n² = n*(n+1)*(2n+1)/6.
      
      Also ist
      ∑ⁿ⁺¹ _k=1 n² = n*(n+1)*(2n+1)/6 + (n+1)².
      
      Was wir zum Nachweis der Behauptung gern sehen möchten, ist, dass
      ∑ⁿ⁺¹ _k=1 n² = (n+1)*((n+1)+1)*(2(n+1)+1)/6.
      
      Dass das eine gleich dem anderen ist, muss man jetzt durch ausmultiplizieren und zusammenfassen nachweisen. Mach das mal, und Du wirst sehen, dass die beiden Formeln gleich sind.
   3. Zeige ∑ⁿ _i=1 i³ = (∑ⁿ _i=1 i )²

      Vollst. Induktion über n.
      n=1: 1=1 ok
      n+1: Es ist ∑ⁿ⁺¹ _i=1 i³ = [ ∑ⁿ _i=1 i³ ] + (n+1)³
      Die Summe bis n kann nach Induktionsvoraussetung ersetzt werden:
      = [ ∑ⁿ _i=1 i ]² + (n+1)³
      und das soll gleich [ ∑ⁿ⁺¹ _i=1 i ]² sein.
      Um das zu sehen, wende ich die Binomische Formel auf
      [ ∑ⁿ⁺¹ _i=1 i ]² = [ (∑ⁿ _i=1 i ) + (n+1) ]² an:
      = [ (∑ⁿ _i=1 i ) ]² + 2(n+1)*(∑ⁿ _i=1 i ) + (n+1)²
      Für die Summenformel in der Mitte setze ich den seit Gauss bekannten Ausdruck ein:
      = [ (∑ⁿ _i=1 i ) ]² + 2(n+1)*1/2*n*(n+1) + (n+1)²
      = [ (∑ⁿ _i=1 i ) ]² + (n+1)*n*(n+1) + (n+1)²
      in den hinteren beiden Summanden klammere ich (n+1)² aus:
      = [ (∑ⁿ _i=1 i ) ]² + (n+1)²* (n + 1)
      = [ (∑ⁿ _i=1 i ) ]² + (n+1)³
      Das war's.

   
   
   4. Zeige ∑ⁿ _k=0 k * (ⁿ_k) = n*2^n-1
      Beweis mit Induktion unter Verwendung der bekannten Beziehung: (ⁿ⁺¹_k) = (ⁿ_k) + (ⁿ_k-1).
      Induktionsvoraussetzung bitte selbst machen.
      Induktionsschritt:
      ∑ⁿ⁺¹ _k=0 k * (ⁿ⁺¹_k)
      = ∑ⁿ _k=1 k * (ⁿ⁺¹_k) + (n+1)
      = ∑ⁿ _k=1 k * [(ⁿ_k) + (ⁿ_k-1)] +(n+1)
      = ∑ⁿ _k=1 k * (ⁿ_k) + ∑ⁿ _k=1 k * (ⁿ_k-1) + (n+1)
      = ∑ⁿ _k=0 k * (ⁿ_k) + ∑^n-1 _k=0 (k+1) * (ⁿ_k) + n + 1
      = ∑ⁿ _k=0 k * (ⁿ_k) + ∑^n-1 _k=0 k * (ⁿ_k) + ∑^n-1 _k=0 (ⁿ_k) + n + 1
      = ∑ⁿ _k=0 k * (ⁿ_k) + ∑ⁿ _k=0 k * (ⁿ_k) + ∑^n-1 _k=0 (ⁿ_k) + 1
      = ∑ⁿ _k=0 k * (ⁿ_k) + ∑ⁿ _k=0 k * (ⁿ_k) + ∑ⁿ _k=0 (ⁿ_k)
      = n*2^n-1 + n*2^n-1 + 2ⁿ
      = 2*n*2^n-1 + 2ⁿ
      = n*2ⁿ + 2ⁿ
      = (n+1)*2ⁿ
      Das war's schon.
      Die Arbeit besteht darin, die Summen ohne Fehler umzuformen und die Indizes zu transformieren.

   

   6. Abschätzungen
      1. Man beweise: n/2 < ∑^2n-1 _i=1(1 / i) < n
         Induktion.
         Anfang: n=2. Stimmt.
         Dann ∑^2n+1-1 _i=1 1/i = ∑^2n-1 _i=1 1/i + ∑^2n+1-1 _i=2ⁿ 1/i
         Die erste Summe kann mit der Induktionsvoraussetzung abgeschätzt werden (nach oben bzw. nach unten). Um die zweite Summe nach oben abzuschätzen, schätze jeden Summanden gegen 1/2²ⁿ ab. Insgesamt sind es 2²ⁿ Summanden, also kann die zweite Summe gegen 1 abgeschätzt werden.
         Folglich ist
         = ∑^2n-1 _i=1 1/i + ∑^2n+1-1 _i=2ⁿ 1/i < n + 1. Das war der eine Teil.
         Und die Abschätzung nach unten: Schätze jeden Summanden der zweiten Summe gegen 1/2ⁿ⁺¹ ab. Es sind 2ⁿ Summanden, also ist die zweite Summe größer als 1/2.
      2. Beweise, dass fur alle natürlichen Zahlen n gilt:
         (1/(1*3))+(1/(3*5))+...+(1/((2n-1)*(2n+1)))<1/2
         Das zeigt man nicht mit vollst. Induktion, wenigstens nicht direkt.
         Man hat ja nichts davon, zu wissen dass S(n)<1/2 ist, wenn man zeigen will, dass S(n+1)<1/2.
         [Ich verwende S(n) als Abkürzung für obige Summe.]
         
         Zur Lösung:
         Ich definiere a(n) = 1/[(2n-1)(2n+1)].
         Und S(n,m)=∑^m _i=n a(i), also die Summe über m-n+1 Folgenglieder, beginnend bei a(m).

         Beispiele
         S(1,1)=∑¹ _i=1 a(i) = 1/3
         S(2,4)=∑⁴ _i=2 a(i) = 1/15 + 1/35 + 1/63 = 1/9
         S(5,12)=∑¹² _i=5 a(i) = 1/27
         Die Anzahl der Summanden je Summe ist 1, 3, 9.
         Von vorne beginnend kann man jeweils die nächsten 3^k Summanden addieren (k≥0) und deren Summe ist gleich 1 / 3^k+1.
         Also:
         Die ersten 3⁰ Summanden addiert, ergibt 1/3¹.
         Die nächsten 3¹ Summanden addiert, ergibt 1/3².
         usw.
         
         Es läuft darauf hinaus, dass ∑ⁿ _i=1 a(i) <= ∑^x _k=0 S(y,z) = ∑^x _i=1 (1/3)ⁱ. Das ist eine geometrische Reihe mit q=1/3, der nur der i=0-Term fehlt. Mit 0-Term ist die Summe der geom. Reihe gleich (1-qⁿ)/(1-q). Ohne 0-Term ist die Summe (1-qⁿ)/(1-q) - 1. Mit q=1/3 kann man hier zeigen, dass das immer kleiner 1/2 ist.
         
         Was muss man nun noch tun?
         1. Eine Berechnungsvorschrift für x, y und z in ∑ⁿ _i=1 a(i) <= ∑^x _k=0 S(y,z) angeben.
         2. Mit Induktion beweisen, dass diese Summen für die passenden x,y,z gleich 1/3^? ist.
         
         Versuch mal, was Du auf diese Art erreichen kannst.
         Der Ansatz für den Beweis ist, dass man - wie ich schon geschrieben habe - die Summanden zu Gruppen zusammenfasst (immer 3k Summanden, also erst 1, dann 3, dann 9 usw.) und für jede Teilsumme (die nenne ich S(i,j)) zeigt, dass sie kleiner oder gleich etwas ist. Dabei hat man es mit sehr unangenehmen Indexrechnungen zu tun. Aber um zu verstehen, was ich meine, kannst Du ja mal die Teilsummen bilden. Auch wenn Du das dann nicht formal hinbekommst, hast Du dennoch etwas verstanden.

   7. Teilbarkeit

   1. Beweise: 47 ist ein Teiler von 7⁽²ⁿ⁾ - 2ⁿ

      Der Induktionsanfang ist klar
      n=1 => 7² - 2¹ = 47; 47 ist Teiler von 47
      und die Induktionsbehauptung auch: A(n+1): 47 ist ein Teiler von 7⁽²ⁿ⁺²⁾ - 2⁽ⁿ⁺¹⁾
      Wie kann ich diesen Ausdruck vereinfachen, so dass eine Aussage stehen bleibt, von der auch 47 Teiler ist.

      Ganz einfach:
      7²ⁿ - 2ⁿ = [7²]ⁿ - 2ⁿ.
      Induktionsschritt:
      [7²]ⁿ⁺¹ - 2ⁿ⁺¹
      = [7²]ⁿ*[7²] - 2ⁿ⁺¹
      Ergänze in der Klammer -2 und hinter der Klammer
      mache das durch +2*[7²]ⁿ wieder gut.
      = [7²]ⁿ*[7²-2] +2*[7²]ⁿ - 2*2ⁿ
      = [7²]ⁿ*[7²-2] + 2*[7²]ⁿ - 2*2ⁿ
      = [7²]ⁿ*[7²-2] + 2*( [7²]ⁿ - 2ⁿ )
      Jeder der beiden Summanden enthält also einen Faktor, der nach Induktionsvoraussetzung durch 47 teilbar ist. Folglich ist der gesamte Ausdruck durch 47 teilbar.

   

   8. Zahlentheorie

   1. Behauptung: Es gibt unendlich viele Primzahlen

      Der geforderte Beweis wird oft durch Widerspruch geführt. Ich will das zunächst auch tun. Als zweiten Beweis gebe ich dann noch den durch vollst. Induktion. Man wird sehen, dass der Widerspruchsbeweis umständlicher ist. Es wird nämlich der Widerspruch genau mit der konstruktiven Idee für die vollst. Induktion erzeugt.

      Wenn es wirklich unendlich viele Primzahlen gibt, kann man sicher nicht alle Primzahlen aufschreiben. Aber man kann die Möglichkeit prüfen, dass es nur endlich viele Primzahlen gibt und diese Möglichkeit konsequent weiter denken. Am Ende dieser Überlegung wird man feststellen, dass etwas nicht stimmt. Und wenn ein aufgrund logischer Gesetze entstandenes Endergebnis offensichtlich nicht wahr sein kann, ist erwiesen, dass auch die am Anfang getroffene Annahme nicht wahr sein kann. Aus etwas richtigem kann nach der mathematischen Logik niemals etwas falsches folgen. Diese Beweistechnik nennt man einen Widerspruchsbeweis.

      Angenommen es gäbe nur endlich viele Primzahlen p₁,....,p_n.
      Dann betrachte die Zahl p=p₁*...*p_n+1, welche offensichtlich durch keines der p_i, i=1,...,n teilbar ist. Dann muss p, welches ja von allen p_i verschieden ist, offensichtlich eine Primzahl sein.
      Das ist ein Widerspruch zur Annahme.
      Also war die Annahme falsch, es muss demnach unendlich viele Primzahlen geben.

      Der Beweis enthält eine konstruktive Idee, wie man aus den ersten n Primzahlen eine weitere Zahl konstruieren kann, durch die man die Existenz einer weiteren, der (n+1)-ten Primzahl, nachweisen kann .
      Anstatt einen Beweis durch Widerspruch zu führen, hätte man auch den direkten Beweis führen können. Der geht dann so:

      Es seien die ersten n Primzahlen bekannt. Dann betrachte Zahl q = p₁*...*p_n+1, welche offensichtlich durch keines der p_i, i=1,...,n teilbar ist.

      Wir wissen nicht, ob q eine Primzahl ist, darum betrachten wir jetzt beide Möglichkeiten.
      Fall 1: q ist eine Primzahl. Dann haben wir eine weitere Primzahl gefunden.
      Fall 2: q ist keine Primzahl. Dann gibt es einen echten Teiler von q. (Ein echter Teiler ist weder die 1 noch q selbst).
      Diese Teiler ist nach Konstruktion von q keine der Primzahlen p₁, ... , p_n. Es muss demnach eine weitere Primzahl geben, die q teilt. Diese "andere" Primzahl ist größer als p_n. Ich nenne diese neue Primzahl p^*. p^* ist nicht notwendigerweise die n+1 -te Primzahl (es kann zwischen der größten Primzahl unter den ersten n Primzahlen und der neuen Primzahl noch andere Primzahlen geben), aber aus der Existenz von n Primzahlen folgt die Existenz von mindestens n+1 Primzahlen. Diese Art zu schließen ist die vollständige Induktion. Als Induktionsanfang genügt die Existenz einer Primzahl. Ausgehend von p₁=2 weist man so die Existenz einer weiteren Primzahl nach.

      Wer sich nun fragt, ob denn q nicht immer eine Primzahl ist, dem gebe ich ein Gegenbeispiel:
      2 * 3 * 5 * 7 * 11 * 13 + 1 = 30031 ist keine Primzahl, denn 30031 = 59 * 509.

      Im Induktionsschritt muss man deshalb vorsichtig sein.
      Aus den ersten n Primzahlen p₁,....,p_n ergibt sich die Existenz einer weiteren. Wie diese neue Primzahl aber lautet, sagt der Beweis nicht.
      Und die Primzahl p^* ist nicht notwendig die (n+1)-te Primzahl. Aber wenn es bis zu p^* mehr als n+1 Primzahlen gibt, dann ist das ja auch genug. Man sucht dann aus den mehr als n+1 Primzahlen die ersten n+1 heraus und kann damit den Induktionsschritt von n+1 auf n+2 durchführen.

   9. Rekursiv definierte Folgen

   1. Für die Fibonacci Zahlen u₁=1, u₂=1 und u_n+1=u_n + u_n-1, n ∈ N ist zu zeigen:
      u_n+m = u_n-1*u_m + u_n*u_m+1
      Beweis mit Induktion über m.
      Für m=1 also u_n-1*u₁ + u_n*u₂
      = u_n-1*1 + u_n*1 = u_n-1 + u_n. OK.
      Nun u_n+(m+1) = u_n+m + u_n+m-1
      Für u_n+m und u_n+m-1 die Induktionsvoraussetzung anwenden, vereinfachen, umsortieren usw. Führt zum Ergebnis.
   2. Die Folge a(n) sei rekursiv definiert durch die folgende Formel:
      
      a(n+1) = 1 + 2a(n-1) + ∑^n-1 _k=0 a(k)
      Bestimme eine explizite Formel für a(n) (für alle n ∈ N⁺).

      Anfangswerte sind a(0) = 1
      a(1) = 2
      Ich rechne zuerst einige weitere Folgenglieder aus:
      a(2) = 1 + 3*a(0) + ∑^-1 _k=0 a(k)
      Die Summe hat also keine Summanden!
      => a(2) = 1+3*1 = 4
      
      a(3) = 1 + 3*a(1) + ∑⁰ _k=0 a(k)
      Die Summe hat nur einen Summanden: k=0!
      => a(3) = 1+3*a(1) + a(0) = 1 + 3*2 + 1 = 8
      
      a(4) = 1 + 3*a(2) + ∑¹ _k=0 a(k)
      Die Summe hat zwei Summanden: k=0 und k=1!
      => a(4) = 1+3*a(2) + a(0) + a(1) = 1 + 3*4 + 1 + 2 = 16
      
      a(5) = 1 + 3*a(3) + ∑² _k=0 a(k)
      => a(5) = 1+3*a(3) + a(0) + a(1) + a(2) = 1 + 3*8 + 1 + 2 + 4 = 32
      
      Das sieht so aus, als ob a(n) = 2ⁿ sein könnte.
      Diese Vermutung habe ich durch die ersten berechneten Folgenglieder gefunden.
      
      Ich weiß noch nicht, ob diese Vermutung richtig ist, aber ich will versuchen sie zu beweisen.
      Wenn ich a(n) = 2ⁿ beweisen kann, dann habe ich die geforderte Formel für a(n).
      
      Beweis mit vollständiger Induktion.
      Die Behauptung a(n) = 2ⁿ ist richtig für n=1,2,3,4 und 5 (wie man oben gesehen hat).
      Nun zum Induktionsschritt. Wir wissen, dass für alle n≤n₀ gilt: a(n) = 2ⁿ.
      
      a(n+1) = 1 + 2a(n-1) + ∑^n-1 _k=0 a(k) = 1 + 2*2^n-1 + ∑^n-1 _k=0 2^k
      
      Die Summe ∑^n-1 _k=0 2^k ist gleich (2ⁿ-1)/(2-1). Diese Formel ist bekannt, denn es handelt sich um eine geometrische Reihe mit q=2.
      
      Das setze ich ein:
      a(n+1) = 1 + 2*2^n-1 + (2^n-1-1)/(2-1) = 1 + 2*2^n-1 + 2ⁿ - 1 = 2ⁿ + 2ⁿ = 2ⁿ⁺¹
      Genau das wollten wir zeigen.
      Also gilt für alle n: a(n) = 2ⁿ

   3. Gegeben ist die Folge: a₁= 2, a_n+1=2-1/a_n.
      Zeige a_n=(n+1)/n

      Die schwierigere Frage bei rekursiv definierten Folgen ist die, wie man eine geschlossene Form findet. In dieser Aufgabe ist die Vermutung a_n=(n+1)/n nach einigen ausgerechneten Werten leicht zu raten.
      Um jetzt die Vermutung zu beweisen, muss man nichts besonderes beachten. Ziel ist eine vollständige Induktion.
      Für n=1 ist die Behauptung wahr.
      Und nun der Schluss von n auf n+1.
      Wenn also die Behauptung a_n=(n+1)/n wahr ist,
      dann ist jetzt zu zeigen, dass auch a_n+1=(n+2)/(n+1) wahr ist.
      
      Wegen der rekursiven Definition ist a_n+1=2-1/a_n. [*]
      Und nach Voraussetzung der vollständigen Induktion hier: a_n = (n+1)/n. [**]
      Gleichung [**] in [*] einsetzen, umformen und umordnen, dann steht da
      a_n+1=2-n/(n+1) = (2n+2-n)/(n+1) ) (n+2)/(n+1).
      Das war zu zeigen.
      
      Das Problem bei dieser Aufgabe ist eher, dass sie sehr einfach ist und man Mühe hat, keinen Beweisschritt auszulassen.
      
      Was waren die Schritte:

      1. Induktionsanfang nachprüfen: a₂
      2. Induktionsbehauptung aufstellen: a_n+1
      3. a_n+1 mittels der gegebenen Rekursion ausdrücken. In dem Ausdruck kommt a_n vor.
      4. a_n durch die für n schon erlaubte Formel ersetzen und in Ausdruck aus 3. einsetzen.
      5. Ersetzen Ausdruck aus 3. umformen, bis man das gewünschte Ergebnis sieht.

   

   10. Eindeutigkeitsbeweis
       1. Zeige, dass die Repräsentation von ganzen Zahlen zur Basis 3 mit den Ziffern {-1,0,1} eindeutig ist!

          Sei n ∈ Z und nehmen wir an, dass es zwei verschiedene Repräsentationen gibt.
          Also einerseits ∑^k _i=0 a_i*3ⁱ = n
          und andererseits ∑^l _i=0 b_i*3ⁱ = n.
          Wir können o.B.d.A annehmen, dass k≥l, ansonsten vertauschen wir eben k und l.
          Außerdem können wir, falls l<k ist, die zweite Summe auch bis k laufen lassen mit Koeffizienten b_i=0 für l<i≤k.
          Dann haben wir in beiden Summen gleich viele Summanden. Jetzt bilde die Differenz:
          ∑^k _i=0 a_i*3ⁱ - ∑^k _i=0 b_i*3ⁱ
          = ∑^k _i=0 (a_i-b_i)*3ⁱ = 0
          Beweise nun, dass die Koeffizienten alle Null sind und zwar durch vollständige Induktion über k.
          k=0 => (a₀-b₀)*1 = 0 => a₀ = b₀
          Nun k->k+1. Hinschreiben, dann umsortieren und schließlich:
          ∑^k _i=0 (a_i-b_i)*3ⁱ = (b_k+1-a_k+1)*3^k+1
          Man sieht, die rechte Seite der Gleichung ist durch 3^k+1 teilbar. Da auf der linken Seite nur kleiner Dreierpotenzen vorkommen
          und außerdem -2 < a_i-b_i < 2 für alle 0≤ i ≤ k, folgt dass b_k+1-a_k+1=0. Auf den Rest der Darstellung wende die Induktionsvoraussetzung an (hat ja Summe bis k). Immer gilt a_i = b_i.
          Fertig.
          Achtung: Hier wurde nicht gezeigt, daß die geforderte Darstellung existiert. Es wurde gezeigt, daß die Darstellung eindeutig ist, falls sie existiert. Wir haben immer noch keine Ahnung, wie man eine solche Darstellung für ein n ausrechnen kann. Mehr war aber nicht verlangt.

   11. Differentialrechnung

   1. Beweis der Potenzregel für ganzzahlige negative Exponenten anhand der Quotienten- und Kettenregel:
      Die Ableitung von f(x)=x^-n ist f'(x)=-n*x^-n-1

      Die Funktion f(x)=x^-n=1/xⁿ kann man auch schreiben als f(x)=g(x)/h(x) mit g(x)=1 und h(x)=xⁿ.
      Die Quotientenregel sagt f'(x)=[g'(x)*h(x)-g(x)*h'(x)]/(h(x))²
      Wenn schon als bekannt benutzt werden darf, daß h'(x)=n*x^n-1, dann erhält man:
      f'(x) = [0*h(x)-1*n*x^n-1]/x²ⁿ = -n*x^n-1/x²ⁿ = -n/xⁿ⁺¹ = -n*x^-n-1
      
      Wenn h'(x)=n*x^n-1 auch bewiesen werden soll, dann mache das mit Induktion unter Verwendung der Produktregel.

      Bemerkung:
      Ich drücke die Funktion f(x) als Quotient der Funktionen g(x)/h(x) aus.
      Die Regel für die Ableitung von Quotienten ist schon bekannt, und ich benutzte sie.
      Der Sinn dieses Ansatzes ist, die negativen Exponenten in positive Exponenten von Funktionen im Nenner eines Quotienten zu verwandeln.
      Dann setze ich für g, g', h und h' die jeweiligen Ableitungen ein. Für g(x)=1 ist g'(x)=0. Für h(x)=xⁿ ist h'(x)=n*x^n-1.
      Mit etwas Termumformung und den Potenzrechenregeln (x^n-1/x²ⁿ ist gleich 1/xⁿ⁺¹, denn 2n-(n-1) ist n+1) komme ich dann zum Ergebnis.
      Und auch wegen der Potenzrechenregeln ist (xⁿ)² = (x²ⁿ)

   

10. Zum Schluss

    Das Induktionsargument ist in fast allen Gebieten der Mathematik verbreitet. Je fortgeschrittener aber das Thema, desto kürzer fallen die Beweise aus oder werden gar nicht mehr ausgeführt. Evtl. schreibt der Autor einer mathematischen Arbeit noch "Kann man durch Induktion zeigen". Wie einige meiner Beispiele zeigen, erfordern ausführliche Induktionsbeweise einigen Platz. Den spart man sich häufig zugunsten der Lesbarkeit von mathematischen Texten. Auch hat man in den Publikationsblättern ja oft nur wenige Seiten zur Verfügung. Die Arbeit, die veröffentlicht werden soll, muss gegenüber der vorhandenen Ausarbeitung deutlich gekürzt werden.
    Das Induktionsprinzip ist von Mathematikern derart verinnerlicht, dass sie es intuitiv schon sehen, wo und wie eine Induktion angesetzt werden kann und dankbar sind für die Auslassung unnötiger Details. Es genügt die Beschreibung der Idee ("füge eine neue Gerade hinzu ...") um einen Beweis zu geben, bzw. es genügt, den ausführlichen und genauen Beweis in der Hinterhand zu haben, falls irgendwelche Zweifel an der Richtigkeit auftauchen.

    Weiterführende Links bei Matroids Matheplanet.

    Sehr schöne und von der Idee her abwechslungsreiche Induktionsbeweise gibt es auch in der Kombinatorik und Graphentheorie (Induktion über die maximale Valenz einer Ecke). Vielleicht schreibe ich darüber das nächste mal.

-- 10 9 8 7 6 5 4 3 2 1

Dieser Artikel ist in unserem Buch enthalten: Mathematisch für Anfänger