- Die Frage
- Verstehe das Problem
- Suche Zusammenhänge und ersinne einen Plan
- Führe den Plan aus
- Überprüfe die gefundene Lösung
- Verstehe das Problem
- Beispiel
- Erste (falsche) Lösung:
- Systematisches Probieren
-
Suche Zusammenhänge, ersinne einen Plan und führe ihn aus
- Suche im Internet
- Man kann nicht die Sitzordnungen an einem geraden Tisch zählen und durch die Anzahl der Personen teilen.
- Wenn man statt einer nicht ganzzahliger Lösungen die nächstgrößere ganze Zahl als Lösung vermutet, dann stimmt das zwar für m = f = 3 aber nicht allgemein.
- Eine Wertetabelle
- Ein Plan
-
Überprüfe die Lösung
- Das Burnside Lemma
- Anwendung des Polya-Burnside Lemmas
- Die T(n,k)-Formel
- Verstehe die Formel
- Gruppe der Rotationen
- Unterscheidungen bei der Fragestellung
-
Am Ziel
- Zwei verschiedene Berechnungsweisen?
- Lösung der Aufgabe
- Konstruktiver Algorithmus?
- Nachbetrachtung
- Quellen
| Um einen Kreis sollen a Elemente der Art A und b Elemente der Art B angeordnet werden. Kombinationen, die durch Drehung auf sich selbst abgebildet werden können, werden nur einmal gezählt! Wieviele Möglichkeiten gibt es? |
Ich suche eine Antwort zu geben. Dabei bin ich schließlich fündig geworden.
Ich möchte hier berichten, wie ich vorgegangen bin und nicht zuletzt, die Lösung geben.
| Inhalt: |
| 1 Die Frage * |
| 2 Der Weg * |
| 3 Verstehe das Problem * |
| 3.1 Beispiel * |
| 3.2 Erste (falsche) Lösung: * |
| 3.3 Systematisches Probieren * |
| 4 Suche Zusammenhänge, ersinne einen Plan und führe ihn aus * |
| 4.1 Suche im Internet * |
| 4.2 Eine Wertetabelle * |
| 4.3 Ein Plan * |
| 5 Überprüfe die Lösung * |
| 5.1 Das Burnside Lemma * |
| 5.2 Anwendung des Polya-Burnside Lemmas * |
|
5.3 Die T(n,k)-Formel * |
| 5.4 Verstehe die Formel * |
| 5.5 Gruppe der Rotationen * |
| 5.6 Unterscheidungen bei der Fragestellung * |
| 6 Am Ziel * |
| 6.1 Zwei verschiedene Berechnungsweisen? * |
| 6.2 Lösung der Aufgabe * |
| 6.3 Konstruktiver Algorithmus? * |
| 6.4 Nachbetrachtung * |
| 7 Quellen * |
George Polya (1887-1985) hat in seinem Buch "How to solve it" [Polya] einige Regeln aufgestellt, die beim plausiblem Schließen eine große Hilfe sein können.
Ausführlicher findet man das z.B. bei E. Specht: http://hydra.nat.uni-magdeburg.de/geom/PZ.html
Kurz gefaßt lauten diese Regeln:
Das ist ein sehr allgemeiner Weg. Aber wie es so ist, ist der Weg das Ziel. Also dann ...
Für 3 Männer und 3 Frauen probiere ich einige mögliche Sitzordnungen und stelle schnell fest, daß ich leicht die eine oder andere Drehungsmöglichkeit übersehen kann, wenn ich nicht ein sicheres Unterscheidungsmerkmal für die Anordnungen finde.
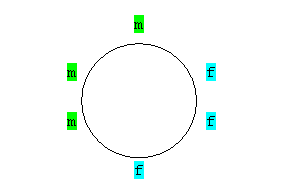
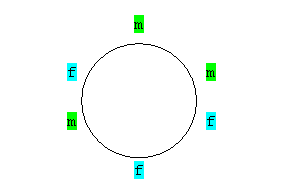
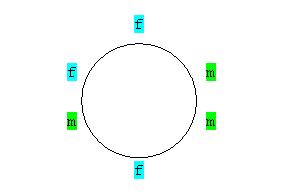
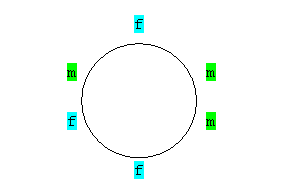
|
Abbildung 1 |
Abbildung 2 |
|
Abbildung 3 |
Abbildung 4 |
Man sieht schon, die Abbildung 2 kann durch eine Drehung um 60° in die Anordnung der Abbildung 4 überführt werden.
Zähle alle Anordnungen von 3+3 Elementen und teile diese Anzahl durch 6, weil 6 ist die Anzahl der Drehungen (nämlich: 60°, 120°, 180°, 240°, 300° und 360° oder 0° als identische Abbildung).
Im Falle m = f = 3 ergibt sich:
6! 1 20
----- * - = --
3!*3! 6 6
Aber das ist keine ganze Zahl. Etwas stimmt nicht.
Durch systematisches Probieren finde ich für m = f = 3 folgende Lösungen:
|
Anordnung Nr. |
Repräsentant |
Anzahl weiterer Repräsentanten (Identität mitgezählt) |
|
1 |
m m m f f f |
6 |
|
2 |
m m f f m f |
6 |
|
3 |
m m f m f f |
6 |
|
4 |
m f m f m f |
2 |
Das sind alle Anordnungen mit m = f = 3, denn entweder sitzen die drei Frauen zusammen (Anordnung 1) oder Männer und Frauen sitzen abwechselnd (Anordnung 4) oder es sitzen 2 Frauen nebeneinander und die dritte sitzt zwischen Männern. Im letzteren Fall muß man die Möglichkeiten unterscheiden, daß hinter zwei Frauen ein Mann (Anordnung 3) oder zwei Männer (Anordnung 2) sitzen. Insgesamt 4 Möglichkeiten.
Für jede Anordnung nennt die Tabelle einen Repräsentanten.
Die Gleichheit von Anordnungen bis auf Drehungen kann als Äquivalenzrelation beschrieben werden:
Zwei Anordnungen a und b sind äquivalent, wenn es eine Drehung gibt, die die eine in die andere überführt.
m m m f f f
ist Repräsentant für die 6 Anordnungen bzgl. dieser Äquivalenzrelation.m m m f f fDiese 6 Anordnungen können durch Drehungen aufeinander abgebildet werden.
m m f f f m
m f f f m m
f f f m m m
f f m m m f
f m m m f f
Der Repräsentant m f m f m f repräsentiert aber nur 2 Anordnungen (incl. sich selbst), nämlich:
m f m f m f
f m f m f m
Nun sieht man auch, warum die erste Lösungsidee nicht funktioniert. Die Anzahl aller Anordnungen ohne Anwendung von Drehungen ist 20 (= 6+6+6+2). Die gesuchte Anzahl ist 4, dafür gibt es 4 Repräsentanten. Aber nicht jede Klasse enthält genau 6 Anordnungen.
Bei der Suche im Internet stieß ich auf [DrMath97], siehe http://mathforum.org/dr.math/problems/lerche5.16.97.html
Dort war die gleiche Frage gestellt. Die Antwort entsprach genau meiner falschen Lösungsidee. Der Fragende hatte das auch bemerkt und einige Nachfragen gestellt.
Schließlich war nur so viel klar:
Auf manchen Seiten im Internet konnte ich die Frage noch als Rätsel finden, etwa mit den Zahlen m = f = 3. Prinzipielles über das Lösungsverfahren oder eine Formel zur Anzahlberechnung wurde da nicht gegeben.
Für verschiedene Werte von m und f habe ich eine Wertetabelle aufgestellt, vor allem um mehr über das Problem zu lernen.
Die Anzahl der Anordnungen von m Männern und f Frauen um einen runden Tisch, bei der durch Drehungen aufeinander abbildbare Anordnungen als gleich angesehen werden, bezeichne ich im folgenden mit A(m,f).
Das Problem ist offensichtlich symmetrisch, d.h. A(m,f) = A(f,m). Darum kann man die Tabelle lesen, wie man möchte. Ich selbst halte es so, in den Zeilen die Anzahl der Männer zu suchen und in den Spalten die Anzahl der Frauen.
Die Tabelle zeigt die Werte A(m,f) für alle Gesellschaften aus bis zu 8 Personen.
A(m,f)
0
1
2
3
4
5
6
7
8
0
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
2
1
1
2
2
3
3
4
3
1
1
2
4
5
7
4
1
1
3
5
10
5
1
1
3
7
6
1
1
4
7
1
1
8
1
Tabelle 1: A(m,f)
Es ist z.B. A(5,0) = 1, denn es gibt nur eine Möglichkeit 5 Männer an einen runden Tisch zu setzen. Es ist A(3,3) = 4, wie oben gezeigt. Die Anzahl A(0,0) dachte ich mir aus Gewohnheit als 1, weil es in der Mathematik i.d.R. eine Möglichkeit gibt, die leere Menge zu bilden (Man denke an 00.)
Die 10 Anordnungen für A(4,4) haben Repräsentanten:
m m m m f f f f
m m m f f f m f
m m f f m f m f
m m f f m f m f
m f m f m f m f
m m m f f m f f
m m m f m f f f
m m f m f m f f
m f m m f m f f
m m f f f m m f
Wer möchte soll die Vollständigkeit und Richtigkeit dieser 10 Anordnungen überprüfen.
Durch eigene Bemühungen fand ich keine schlüssige Zählweise.
Da erinnerte ich mich an eine wunderbare Internetseite, nämlich The On-Line Encyclopedia of Integer Sequences. Das ist eine Repository mit Suchmaschine für Integer-Folgen.
Ich habe nach der Folge gesucht. Quadratisch angeordnete Zahlenwerte sucht man dort durch Aneinanderreihung der Werte der Gegendiagonalen. Ich suchte also nach
1,1,1,1,1,1,1,1,1,1,1,1,2,1,1,1,1,2,2,1,1,1,1,3,4,3,1,1,1,1, 3,5,5,3,1,1,1,1,4,7,10,7,4,1,1,1,1
Und wurde fündig: http://www.research.att.com/cgi-bin/access.cgi/as/njas/sequences/eisA.cgi?Anum=A047996
Der Name der Folge ist dort "Triangle of circular binomial coefficients T(n,k), 0<=k<=n" und die Beschreibung lautet: "T(n,k)=number of necklaces with k black beads, n-k white beads".
Dazu war noch eine Formel angegeben:
T(n,k)=(1/n) * Sum_{d | (n,k)} phi(d)*binomial(n/d,k/d)
Also geht es um Halsbänder (necklaces), die man aus Perlen (beads) von verschiedenen Farben macht.
Was sagt mir diese Formel. Wo ist die Theorie dazu?
Ich vermutete, daß T(n,k) meinem A(m,f) entspricht, wenn man n = m + f und k = f setzt.
Also T(m+f,f) = A(m,f).
Das hat sich dann auch als richtig erwiesen.
Immerhin, was ich gefunden hatte, paßte zur Aufgabe und ließ mich weitersuchen.
Und ich habe an oben genanntem Dr. Math geschrieben. In der wirklich hilfreichen Antwort war dann von dem Burnside Lemma die Rede – und von "dihedral groups", also Dieder-Gruppen. (Siehe auch [DrMath499] und [DrMath299]).
Mit neuen Suchworten versehen, fand ich einmal den mehrfachen Hinweis, daß das Burnside Lemma besser "Polya-Burnside Lemma" oder "Lemma von Cauchy-Frobenius" zu nennen sei.
Siehe dazu:
Lüneburg, Heinz, A Lemma that is not Burnside'sund
http://www.mathematik.uni-kl.de/~luene/miszellen/Burnside.html
Schoenert, Martin, A lemma that is *not* Burnside's http://www.math.rwth-aachen.de/~Martin.Schoenert/Cube-Lovers/Martin_Schoenert__A_lemma_that_is_*not*_Burnside's.html
Und wie lautet das Burnside Lemma?
Eine Formulierung gibt [BettenFK], siehe http://www.mathe2.uni-bayreuth.de/frib/html/book/hyl00.html [Unter Cauchy-Fobenius Lemma)
Dort auch ein Beweis. Aber diese Formulierung ist für Gelegenheitsmathematiker nicht so eingängig. Ich will die Theorie anwenden. Den Beweis haben andere überprüft.
Eine für mich besser geeignete Darstellung fand ich bei [McGowan]: "The number of distinct necklaces" in http://sunmarkinc.com/contest/puzzles2.html.
nämlich:
Polya Burnside Lemma:
If you have a set, S, and a group, G, acting on the set.
For each element s in S, consider G(s) the orbit of s
as the set {g(s): g in G}.
Say two elements, s_1 and s_2, in S are "equivalent" (under G) if there exists a g in G with g(s_1)=s_2.
The equivalence classes under this relation are just the orbits. The number of equivalence classes is given by:
SUM[#(g):g in G]/|G|
where #(g) is the number of elements, s, in S satisfying g(s)=s (the size of g's "fixed set") and |G| is the order (size) of the group G.
[Schon bemerkt: Polya!. Der Weg ist das Ziel.]
Klassen und Repräsentanten hatte ich im Zusammenhang mit dem gestellten Problem schon eingeführt:
Zwei Anordnungen sind äquivalent, wenn es eine Gruppenoperation gibt, die die eine auf die andere abbildet.
Das Polya-Burnside Lemma besagt, daß die Anzahl der verschiedenen Äquivalenzklassen bzgl. dieser Relation gleich der Summe der Anzahlen der Anordnungen ist, die von einer Gruppenoperation auf sich selbst abgebildet werden – geteilt durch die Ordnung der Gruppe.
Die Menge der Anordnungen, die untersucht wird, ist die Menge der n-Tupel aus Männern und Frauen. Die Gruppenoperationen sind Drehungen.
In dem Artikel von [McGowan] wird u.a. folgende Formel gegeben:
SUM[k^GCD(j,n):j=0,1,2...(n-1)]/n
^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^
(Polya Burnside Lemma using the rotation group)
Darin ist GCD der Greatest_Common_Divisor, also das ggt. Das k ist die Anzahl der Farben, die zur Verfügung stehen.
Diese Formel berechnet aber nicht, was ich suche, sondern statt dessen die Anzahl der bis auf Drehungen verschiedenen Halsbänder aus n Perlen von k Farben.
Wenn das aber so ist, dann sollte die von dieser Formel berechnete Anzahl für ein bestimmtes n gleich der Summe der Anzahlen aus meiner A(m.f)-Tabelle für n = m+f sein.
Ich rechne (mit k=2 und n=8):
SUM[2^GCD(j,8):j=0,1,2...7]/n = 288 / 8 = 36
Dabei verwende ich folgende Werte für GCD(j,8) = ggt(j,8):
j
ggt(j,8)
0
8
1
1
2
2
3
1
4
4
5
1
6
2
7
1
Also 2^8 + 2^1 + 2^2 + 2^1 + 2^4 + 2^1 + 2^2 + 2^1 = 288
Auf der anderen Seite lese ich die Werte für A(m,f) mit m+f = 8 aus der Tabelle ab (rot markierte Felder):
A(m,f)
0
1
2
3
4
5
6
7
8
0
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
2
1
1
2
2
3
3
4
3
1
1
2
4
5
7
4
1
1
3
5
10
5
1
1
3
7
6
1
1
4
7
1
1
8
1
Tatsächlich ist die Summe der A(m,f) mit m+f = 8 genau 36. Sehr gut!
Nachdem ich wußte, daß ich erstens auf der richtigen Spur war und zweitens, daß meine A(m,f)-Tabelle anscheinend richtig ist, wagte ich mich auch an die T(n,k)-Formel aus [A047996].
T(n,k)-Formel
T(n,k)=(1/n) * Sum_{d | (n,k)} phi(d)*binomial(n/d,k/d)
Ich berechne T(6,3). Es sollte sich 4 ergeben.
1
T(6,3) = - * S phi(d)* binomial(6/d,3/d)
6 dÎ{1,3}
phi(n) bezeichnet die Eulersche phi-Funktion, also die Anzahl der positiven ganzen Zahlen (1,2,3,....etc) bis und einschließlich n, die zu n relativ teilerfremd sind. Das griechische Symbol für diese Funktion ist f (n). Der Binomialkoeffizient "n über k" wird hier als binomial(n,k) geschrieben.
Beispiele für f (n):
n
f (n)
Erläuterung
1
1
denn 1 ist zu 1 relativ Prim, weil 1 keine Primzahl ist
2
1
3
2
relativ prim sind 1 und 2
4
2
relativ prim sind 1 und 3
5
4
relativ prim sind 1, 2, 3 und 4
Zurück zur Berechnung von T(6,3).
1
T(6,3) = - * S phi(d)* binomial(6/d,3/d)
6 dÎ {1,3}
Die Summe läuft über alle gemeinsamen Teiler von n und k (d|(n,k)}. Das sind für n=6 und k=3 die Zahlen 1 und 3. Mit "binomial(6/d,3/d)" ist der Binomialkoeffizient "6/d über 3/d" gemeint.
Folgt:
1
T(6,3) = - * (phi(1) * binomial(6,3) + phi(3) * binomial(2,1))
6
= 1/6 * ( 20 + 4 ) = 24 / 6 = 4
Und das ist A(3,3).
Die Berechnung für T(8,4)
1
T(8,4) = - * S phi(d)* binomial(8/d,4/d)
8 dÎ {1,2,4}
=> T(8,4) = 1/8 * ( 70 + 1 * 6 + 2 * 2 ) = 80 / 8 = 10
Auch diese Rechnung ergibt das erwünschte Ergebnis.
Schön! Aber warum?
Für m = f = 3, also n=6 möchte ich die verwendete Formel begründen.
Für m = f = 3 findet man 20 Permutationen (bei Zählung von Drehungen). Davon sind höchstens 6 in einer Klasse (d.h. bis auf Drehungen äquivalent).
Wieviele Klassen gibt es mit genau 6 Elementen?
Klassen mit 6 Elementen sind solche, deren Repräsentanten in sich keine Symmetrien durch Drehungen aufweisen..
Beispiel: m f m f m f weist eine interne Drehsymmetrie auf, nämlich um 120°. Dagegen weist m m m f f f keine interne Drehsymmetrie auf.
Die Länge einer internen Drehsymmetrie sei die minimale Länge, des sich in der Anordnung wiederholenden Musters. Ich nenne einen minimalen internen drehsymmetrischen Abschnitt einer Anordnung ein "Muster". Die Anzahl der Wiederholungen des Musters in der gesamten Anordnung nenne ich die Periode des Musters.
Beispiel: In m f m f m f ist das Muster m f ,dessen Länge ist 2 und die Periode des Musters ist 3.
Die Länge des Musters muß ein Teiler von 6 sein!
Folglich kann es nur interne Drehsymmetrien der Länge 2 oder 3 geben.
Es muß gelten: Länge * Periode = m + f = n.
Die interne Drehsymmetrie einer Anordnung erfordert aber auch, daß die Summe der Anzahlen von Männern und Frauen in dem Muster mit Periode d jeweils genau m/d bzw. f/d ist. Für m = f = 3 muß die Anzahl der m’s und f’s in einem Muster mit Periode 2 gleich m/2 = 3/2 bzw. f/2 = 3/2 sein. Das ist nicht möglich. Daran sieht man, daß es kein Muster der Länge 3 gibt.
Es gibt Muster der Länge 2. Deren Periode ist 3 und m/3 = 1 bzw. f/3 = 1.
Wieviele verschiedene Muster aus 2 Personen, ein Mann und eine Frau, gibt es? Das sind 2, nämlich m f und f m.
Die Anordnungen von 3 Männern und 3 Frauen, die keine Muster (also auch keine Periodizität) aufweisen, ergeben unter allen möglichen Drehung jeweils 6 verschiedene Repräsentanten.
Die Anordnungen mit periodischen Mustern, haben weniger als 6 verschiedene Repräsentanten in ihrer Klasse.
Beispiel: : m f m f m f hat nur 2 statt 6 Repräsentanten in seiner Klasse. Es fehlen 4 Repräsentanten, um erfolgreich durch 6 teilen zu können.
Der Sinn der obigen Formel ist nun, die Anzahl der für die Division durch 6 fehlenden Repräsentanten zu ergänzen.
Für Klassen mit periodischen Repräsentanten kommen nur solche in Frage, deren Periode ein gemeinsamer Teiler von n = m + f und k = f ist.
Für n = 6 und k = 3 ist die Menge der gemeinsamen Teiler { 1, 3 }.
Es fehlt die 2 als Teiler.
Durch Addition von phi(3)*binomial(2,1) wird anscheinend die Anzahl der fehlenden Repräsentanten ergänzt.
Soweit meine Überlegung zur Plausibilisierung der Formel.
Das Polya-Burnside Lemma sagt etwas über eine Gruppe aus.
Die Gruppe ist im bisher betrachteten Fall die Gruppe der Rotationen eines regelmäßigen n-Ecks. Die Ordnung dieser Gruppe ist n, denn die Gruppe hat das erzeugende Element r = 360°/n. Es ist r² die Drehung um 2 * 360°/n usw., schließlich ist die identische Abbildung gegeben durch 0 * 360°/n oder n * 360°/n.
Die Ordnung der Gruppe der Rotationen eines 6-Ecks ist 6.
Das Lemma von Polya-Burnside besagt nun, daß die Anzahl der Äquivalenzklassen gleich
SUM[#(g):g in G]/|G|
ist.
Zu bestimmen ist für jede Gruppenoperation die Anzahl der Anordnungen, die durch diese Operation auf sich selbst abgebildet werden.
Durch die Identische Abbildung werden alle Elemente der Gruppe auf sich selbst abgebildet.
Die Elemente der Gruppe sind die Anordnungen aus m Männern und f Frauen.
Für m = f = 3 ist die Anzahl gleich 6!/(3!*3!) = 20.
Durch eine Drehung um 60° wird keine Anordnung auf sich selbst abgebildet, denn dann müßte das Geschlecht aller Personen mit dem des Nachbarn, auf den gedreht wird, übereinstimmen. Damit wären aber alle Personen entweder Männer oder Frauen.
Durch eine Drehung um 120° können Anordnungen mit Mustern der Länge 2 aus jeweils einem Mann und einer Frau auf sich selbst abgebildet werden. Von dieser Art gibt es 2 Anordnungen, denn von den 2 Plätzen des Musters ist einer mit einem Mann oder einer Frau zu besetzen und der andere mit einer Person des anderen Geschlechts. Die übrigen 2 mal 2 Plätze müssen mit dem gleichen Muster aus m‘s und f‘s besetzt werden.
Kombinatorisch: 2! Möglichkeiten.
Durch eine Drehung um 180° können keine Muster auf sich selbst abgebildet werden, weil unter 3 Personen aus 3 Männern und 3 Frauen nicht die Hälfte Männer und die Hälfte Frauen sein können.
Für Drehung um 240° gibt es wiederum 2! Möglichkeiten, denn die Drehung um 240° ist das inverse Element zur Drehung um 120°.
Die Summe der Elemente aller Äquivalenzklassen durch Drehungen ist
20 + 2 + 2
Dies dividiert durch die Ordnung der Gruppe ergibt 4.
Meine Frage betrifft Männer und Frauen an einem runden Tisch. Den Tisch betrachtet man von oben, niemals von unten. Nur durch Drehungen wird die Äquivalenz von Anordnungen definiert.
Im Falle eines Halsbandes hat man die Möglichkeit das Halsband "umzudrehen", geometrisch gesprochen: eine Spiegelung anzuwenden. Dann wären zwei Halsbänder bbrbrr und brbbrr aus 3 roten und 3 blauen Kugeln nicht zu unterscheiden (in einer Äquivalenzklasse).
Wenn bei den Tischordnungen bisher nur Drehungen als Gruppenoperationen in Betracht kamen, dann kann eine Halskette auch Spiegelungen erlauben.
Merke 1:
Wenn man Halsbänder zählt und neben Drehungen auch Spiegelungen als Operationen erlaubt sind, dann bilden alle diese Operationen eine Dieder-Gruppe (dihedral group) der Ordnung 2n (n die Anzahl der Perlen).
Die Dieder-Gruppe der Ordnung 2n ist die Gruppe der ebenen Symmetrieoperationen aus Drehungen und Spiegelungen angewendet auf die n Ecken eines regelmäßigen n-Ecks.
Merke 2:
Wenn man Spiegelungen nicht erlaubt (wie bei Männern und Frauen am runden Tisch), hat man nur die Drehungen zu betrachten.
Beispiel 1:
Für 4 Männer und 4 Frauen, insgesamt 8 Personen, ist die Anzahl der möglichen Sitzordnungen an einem runden Tisch:
1/8 * { 8!/(4!*4!) + 2! + 4!/(2!*2!) + 2! ) = 10
[8 ist die Ordnung der Gruppe der Rotationen eines regelmäßigen 8-Ecks]
Zu bestimmen ist für jede Gruppenoperation die Anzahl der Anordnungen, die durch diese Operation auf sich selbst abgebildet werden.
Für die Drehungen um Vielfache von 360°/8 = 45° sind das
Drehung um ...
Anzahl der invarianten Anordnungen
Identität = 0°
8!
----- = 70
4!*4!r = 45°
nicht möglich
r² = 90°
2!
r³ = 135°
nicht möglich
r4 = 180°
4!
----- = 6
2!*2!r5 = 225°
nicht möglich
r6 = 270° = (r2)-1
2!
r7 = 315°
nicht möglich
Durch die Identische Abbildung werden alle Elemente der Gruppe auf sich selbst abgebildet.
Die Elemente der Gruppe sind die Anordnungen aus m Männern und f Frauen. Deren Anzahl ist 8!/(4!*4!) = 70.
Durch eine Drehung um 45° wird keine Anordnung auf sich selbst abgebildet, denn dann müßte das Geschlecht aller Personen mit dem des Nachbarn, auf den gedreht wird, übereinstimmen. Damit wären aber alle Personen entweder Männer oder Frauen.
Durch eine Drehung um 90° können Anordnungen mit Mustern der Länge 2 aus jeweils einen Mann und einer Frau auf sich selbst abgebildet werden. Von dieser Art gibt es 2 Anordnungen, denn von den 2 Plätzen des Musters ist einer mit einem Mann oder einer Frau zu besetzen und der andere mit einer Person des anderen Geschlechts. Die übrigen 3 mal 2 Plätze müssen mit dem gleichen Muster aus m‘s und f‘s besetzt werden.
Kombinatorisch: 2! Möglichkeiten.
Durch eine Drehung um 135° können keine Muster auf sich selbst abgebildet werden.
Usw.
Die Summe der Elemente aller Äquivalenzklassen durch Drehungen ist
8!/(4!*4!) + 2! + 4!/(2!*2!) + 2! = 80
Division durch die Gruppenordnung ergibt: 80 / 8 = 10.
Beispiel 2:
Die Anzahl verschiedener Halsbänder mit 4 blauen und 4 roten Perlen ist:
1/16 * (8!/(4!*4!) + 2! + 4!/(2!*2!) + 2! + 4 * 4!/(2!*2!) + 4 * 4!/(2!*2!) ) = 8
[Die Ordnung der Dieder-Gruppe für ein 8-Eck ist 2n = 16.]
Zu bestimmen ist für jede Gruppenoperation die Anzahl der Anordnungen, die durch diese Operation auf sich selbst abgebildet werden.
Zu diesen Operationen gehören die Drehungen, die schon im vorigen Beispiel gezählt worden sind.
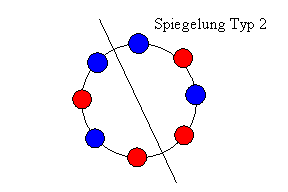
Außerdem sind Spiegelungen zu betrachten. Da die Anzahl der Perlen gerade ist, gibt es zwei verschiedene Arten die Spiegelachse zu legen, nämlich einmal durch zwei gegenüberliegende Perlen (Typ 1) und zum anderen durch zwei gegenüberliegende Zwischenräume (Typ 2). Für beide Typen gibt es jeweils 4 Möglichkeiten die Spiegelachse zu legen.
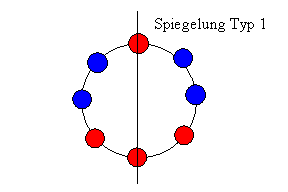
Für eine Spiegelung vom Typ 1 gibt es 24 Anordnungen, die auf sich selbst abgebildet werden. Die beiden Perlen auf der Spiegelachse müssen von der gleichen Farbe sein (2 Möglichkeiten). Von den drei Plätzen auf einer Seite der Spiegelachse wird einer ausgewählt, der die gleiche Farbe erhält, wie die Perlen auf der Spiegelachse (3 Mögl.).
Insgesamt gibt es 4 Spiegelachsen => 2 * 3 * 4 = 24
Spiegelungen vom Typ 2 lassen 24 Anordnungen unverändert.
Auf jeder Seite der Spiegelachse müssen sich gleich viele rote und blaue Kugeln befinden, also jeweils 2. Es gibt 6 Möglichkeiten solche Anordnungen aus 2 roten und 2 blauen Perlen zu bilden. Weil es 4 Spiegelachsen gibt, wird mit 4 multipliziert. => 6 * 4 = 24
Die Summe der je Gruppenoperation (Drehungen und Spiegelungen) auf sich selbst abgebildeten Anordnungen ist
70 + 24 + 24 = 128
Die Ordnung der Gruppe ist 16.
Die Anzahl der Äquivalenzklassen bzgl. der Gruppenoperationen ist 128/16 = 8.
Es gibt 8 verschiedene Perlenketten aus 4 roten und 4 blauen Kugeln.
Oben hatte ich zunächst die T(n,k)-Formel zur Berechnung der Anzahl der Sitzordnungen benutzt. Anschließend hatte ich die gleiche Anzahl über die Auflistung der Gruppenoperationen und die Anzahl der jeweils auf sich selbst abgebildeten Anordnungen bestimmt. Die Ergebnisse stimmen überein.
Die T(n,k)-Formel ergab für m = f = 3, also n = 6:
T(8,4) = 1/8 * ( 70 + 1 * 6 + 2 * 2 ) = 80 / 8 = 10
Bei der Zählweise über die Auflistung der Gruppenoperationen hatte ich mit Teilbarkeiten und Nicht-Teilbarkeiten argumentiert.
1/8 * ( 70 + 2 + 6 + 2 ) = 10
Die T(n,k)-Formel formalisiert diese Teilbarkeitsargumente für den Fall der Rotationsgruppe.
Die Anzahl der Sitzordnungen von n Personen mit k Frauen und n-k Männer am runden Tisch ist gleich T(n,k).
T(n,k)-Formel
T(n,k)=(1/n) * Sum_{d | (n,k)} phi(d)*binomial(n/d,k/d)
Ich suchte noch einen Algorithmus, der alle möglichen Sitzordnungen bzw. alle möglichen Perlenketten erzeugt.
Schließlich habe ich einen gefunden und mit PHP neu implementiert. Zum Halsband-Generator.
Die Aufgabe führte mich in die Algebraische Kombinatorik oder Polya-Theorie.
Zitat [Paule]:
Viele kombinatorische Situationen und Objekte können durch Operationen von Gruppen auf Mengen in natürlicher Weise beschrieben werden. Anwendungen dieses vereinheitlichenden algebraischen Konzeptes (sog. Polya-Theorie) ergeben sich sowohl für Abzählungs- und Klassifikationsprobleme (z.B. chemische Moleküle) als auch für die Konstruktion bzw. Auflistung kombinatorischer Objekte (z.B. Listingalgorithmen für Permutationen, Partitionen, Graphen u.s.w.).
Ich habe die Theorie nur soweit angesehen, wie es für diese Aufgabe erforderlich war.
Bei [Paule], siehe http://www.risc.uni-linz.ac.at/research/combinat/risc/lectures/algorithmic-comb-g.html, findet man Hinweise auf grundlegende Literatur zum Thema.
Die von mir herangezogenen Quellen habe ich im folgenden aufgelistet.
[McGowan]
McGowan, John, The number of distinct necklaces
http://sunmarkinc.com/contest/puzzles2.html
[DrMath499]
Ask Dr. Math, Permutations in a Necklace
http://mathforum.org/dr.math/problems/romer07.04.99.html
April 1999
[DrMath299]
Ask Dr. Math, Polya-Burnside Lemma
http://mathforum.org/dr.math/problems/linger.7.02.99.html
Februar 1999
[DreesSieben}
Drees, Andreas, Siebeneicher, Christian, Ein Lemma über Perlenketten
http://www.mathematik.uni-bielefeld.de/~sieben/lothar/perlenketten.pdf
[BettenFK}
Betten, A., Fripertinger, H., Kerber, A., Algebraic Combinatorics
Via Finite Group Actions
http://bedvgm.kfunigraz.ac.at:8001/frib/html2/book/hyl00.html
September 7, 1998
[Schoenert}
Schoenert, Martin, A lemma that is *not* Burnside's
http://www.math.rwth-aachen.de/~Martin.Schoenert/Cube-Lovers/Martin_Schoenert__A_lemma_that_is_*not*_Burnside's.html
Dezember 7, 1994
[Luene]
Lüneburg, Heinz, A Lemma that is not Burnside's
http://www.mathematik.uni-kl.de/~luene/miszellen/Burnside.html
[DrMath97]
Ask Dr. Math, Combinatorics
http://mathforum.org/dr.math/problems/lerche5.16.97.html
Mai 1997
[A047996]
On-Line Encyclopedia of Integer Sequences - Sequence A047996
http://www.research.att.com/cgi-bin/access.cgi/as/njas/sequences/eisA.cgi?Anum=A047996
[Polya]
Polya, G.: How To Solve It – A New Aspect of Mathematical Method, Second Edition, Princeton University Press, Princeton, New Jersey, 1988. Zitiert nach http://hydra.nat.uni-magdeburg.de/geom/PZ.html
[Paule]
Vorlesungsankündigung "Algorithmische Kombinatorik"
http://www.risc.uni-linz.ac.at/research/combinat/risc/lectures/algorithmic-comb-g.html