
|

|
Bei geometrischen Konstruktionen muss man häufig „Rechte Winkel“ einzeichnen, d.h. zu einer gegebenen Richtung die orthogonale Richtung finden. 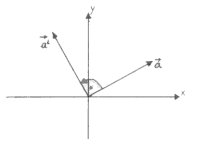
Man kann das so lösen, indem man den vorgegebenen Richtungsvektor um +90° nach links kippt. Man erhält so die Links-Kipp-Regel :
Analog erhält man die Rechts-Kipp-Regel :
Man sieht, dass Die Koordinaten eines gekippten Vektors erhält man also, indem man die Koordinaten des gegebenen Vektors vertauscht und das Vorzeichen einer Koordinate ändert. Zum Festlegen der zu einem
Vektor
Zu einem gegebenen Vektor
gibt es daher unendlich viele Orthogonalvektoren. |
||||||||
|
|
|
|||||||
|
Um festzustellen, ob zwei Vektoren orthogonal sind, ist die Kippregel nicht geeignet. Dazu benötigt man eine andere Regel. Nach oben gilt: 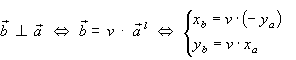
Eliminiert man v, so erhält
man: Die Zahl
Man erhält also: Orthogonalitätskriterium für Vektoren: Zwei Vektoren sind genau dann orthogonal, wenn ihr Skalares Produkt gleich Null ist; d.h.: Beachte, dass gemäß diesem Kriterium der Nullvektor zu jedem Vektor orthogonal ist; solche „Orthogonalvektoren“ werden im Allgemeinen aber nicht verwendet. Rechenregeln und Eigenschaften: Für zwei beliebige
Vektoren
|
||||||||
|
|
|
|||||||
|
Geraden kann man auf verschiedene Weisen darstellen. Wenn man zwei Punkte der Geraden kennt, dann ist die beste Darstellungsweise die Zwei-Punkt-Form der Parameterdarstellung einer Geraden g: 
Jedem Punkt der Geraden
g ist genau ein Parameterwert t Zwei gegebenen Parameterdarstellungen
sieht man nicht sofort an, ob sie die gleiche oder zwei verschiedene
Geraden beschreiben. Eine wichtige Rolle spielen dabei die (unendlich
vielen) Richtungsvektoren einer Geraden. Ein Richtungsvektor wird
zum Beispiel durch den Pfeil 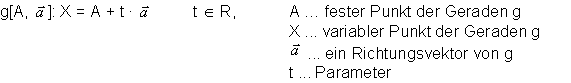
Beachte: Ein Richtungsvektor
darf durch einen „einfacheren“, zu ihm parallelen Richtungsvektor
ersetzt werden. Ortspfeile (d.h. feste Punkte) dürfen hingegen
nicht vereinfacht werden. |
|
|||||||
|
|
|
|||||||
|
1. Lage eines Punktes zu einer Geraden Anschaulich ist klar, dass es nur zwei Möglichkeiten gibt, wie ein Punkt und eine Gerade zueinander liegen können. Entweder liegt der Punkt auf der Geraden oder nicht. Das Inzidenzkriterium besagt: Ein Punkt gehört einer Punktmenge genau dann an, wenn seine Koordinaten die die Punktmenge beschreibende Zuordnungsgleichung erfüllen. Einfacher gesagt heißt das: Ein Punkt liegt genau dann auf einer Geraden, wenn seine Koordinaten die gegebene Parameterdarstellung oder Geradengleichung erfüllen. Beispiel: Liegt
der Punkt A (1 / 0) auf der Geraden g: X = (-1 / 3) + t
·
(2 / -3)?
1 = -1 + 2t => t = 1 2. Lage zweier Geraden zueinander Sind zwei Geraden g und h durch ihre Parameterdarstellungen
gegeben, so kommen
für ihre Lage zueinander folgende Fälle in Frage:
Aus diesen Eigenschaften ergibt sich nun folgender Entscheidungsweg zur Lagebestimmung Zuerst überprüft man, ob die beiden Richtungsvektoren Vielfache sind. Ist dies nicht der Fall, so schneiden die beiden Geraden einander. Sind die Vektoren Vielfache, dann sind die Geraden entweder identisch oder parallel. Um dies heraus zu finden, überprüft man, ob der Punkt der einen Geraden auch auf der anderen liegt. Wenn der Punkt auf der Geraden liegt, so sind die Geraden identisch. Liegt der Punkt nicht auf der anderen Geraden, so sind die untersuchten Geraden zueinander parallel. Schneiden die beiden Geraden einander, so muss man noch den Schnittpunkt berechnen. Beispiel: Untersuche, wie die Geraden g und h zueinander liegen und ermittle gegebenenfalls den Schnittpunkt! g: X = (-1 / -5) + t · (4 / 3); h: X = (1 / 2) + s · (1 / -2) 4 =
v ·
1
v = 4 Da der Schnittpunkt S sowohl auf g als auch auf h liegen soll, kann man S in beide Parameterdarstellungen einsetzten und diese dann gleichsetzen. S (-1 / -5) + t · (4 / 3) = (1 / 2) + s · (1 / -2) Zur Berechnung der Unbekannten formt man um zu: -1 +
4t = 1 + s Durch lösen des Gleichungssystems erhält man t = 1 und s = 2. Nun setzt man t in die Parameterdarstellung von g (bzw. s in die Parameterdarstellung von h) ein und erhält den Schnittpunkt S (3 / -2).
|
||||||||
|
|
|
|||||||
|
Neben der Hauptform der Geradengleichung und der Parameterdarstellung einer Geraden gibt es noch die allgemeine Geradengleichung a · x + b · y = c. Diese drei Darstellungen stehen natürlich in einem Zusammenhang und man kann eine Darstellung in eine andere „umrechnen“. 1. Parameterdarstellung => allgemeine Geradengleichung => Hauptform Der Übergang von der Parameterdarstellung zur allgemeinen Geradengleichung erfolgt durch das Eliminieren des Parameters. Durch das „Explizitmachen“ von y gelangt man von der allgemeinen Geradengleichung zur Hauptform. Beispiel: Beschreibe die Gerade g: X = (-1 / -5) + t · (4 / 3) durch eine allgemeine Geradengleichung und durch die Hauptform. x = -1 + 4
·
t | ·
3 3 ·
x = -3 + 12 ·
t 3 · x – 4 · y = 17 Aus dieser Gleichung erhält man die Hauptform y = ¾ · x – 17/4 2. Hauptform => Parameterdarstellung Bei diesem Übergang ist folgende Regel hilfreich: Steigungs-Richtungs-Regel
: Zwischen der Steigung k und jedem Richtungsvektor Beispiel: Gib eine Parameterdarstellung der durch y = 0,5x – 6 gegebenen Geraden an! k =
0,5 => 3. Allgemeine Geradengleichung => Parameterdarstellung Es gibt zwei Möglichkeiten dieses Problem zu lösen: 1. Man
wandelt die allgemeine Geradengleichung in die Hauptform um und
verwendet dann die Steigungs-Richtungs-Regel. |
|
Zum Seitenanfang
Zum Lexikon Zur Galerie Zum Kapitel Gleichungen der Galerie Zum Inhaltsverzeichnis der Mathematischen Hintergründe Zu den interaktiven Tests Zu den Mathe-Links und Online-Werkzeugen Zur Welcome Page |