Produktregel
Betrachtet werden zwei Funktionen, u(x) und v(x), die differenzierbar sind. Ziel
ist nun, zu zeigen, daß auch das Produkt der beiden Funktionen f(x) = u(x) ![]() v(x), und eine allgemeine Regel für die Ableitung eines Produkts herzuleiten.
Da u(x) und v(x) differenzierbar sind, muß
v(x), und eine allgemeine Regel für die Ableitung eines Produkts herzuleiten.
Da u(x) und v(x) differenzierbar sind, muß
![]()
und
![]()
existieren.
Die Funktion f(x) hat den Differenzenquotienten
![]()
Den Differenzenquotienten von f(x) kann man auch durch die Differenzenquotienten von u(x) und v(x) ausdrücken:
![]()
![]()
![]()
Da die Funktionen u(x) und v(x) differenzierbar sind, folgt für h![]() 0:
0:
![]()
![]()
![]()
Damit ist folgender Satz bewiesen:
Satz: Produktregel
Sind die Funktionen u(x) und v(x) differenzierbar, so ist auch die Funktion f(x)
= u(x) ![]() v(x) differenzierbar, und es
gilt:
v(x) differenzierbar, und es
gilt:
![]() .
.
Veranschaulichung der Produktregel:
Die Herleitung der Produktregel kann mit folgender Grafik veranschaulicht werden.
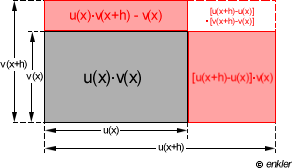
u(x) und v(x) seien Polynomfunktionenm, die in dem betrachteten Bereich positiv sind und monoton wachsen. Die Funktionswerte werden als Seiten des Rechtecks gedeutet. Aus dem Bild ist zu ersehen:
u(x+h) ![]() v(x+h) - u(x)
v(x+h) - u(x) ![]() v(x)
v(x)
= [u(x+h) - u(x)] ![]() v(x) + u(x)
v(x) + u(x) ![]() [v(x+h) - v(x)] + [u(x+h) - u(x)]
[v(x+h) - v(x)] + [u(x+h) - u(x)] ![]() [v(x+h) - v(x)]
[v(x+h) - v(x)]
Zunächst kürzt man mit h, dann setzt man h = 0 und erhält:
(u ![]() v)´(x) = u´(x)
v)´(x) = u´(x) ![]() v(x) + u(x)
v(x) + u(x) ![]() v´(x) + u´(x)
v´(x) + u´(x) ![]() 0
0