Elementare Ableitungsregeln

Grundlegendes

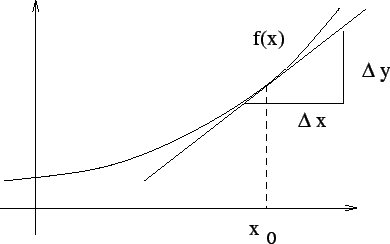
Wir betrachten eine Funktion. Wir möchten nun einen Ausdruck für die lokale Steigung der Funktion an einer bestimmten Stelle finden. Diese lokale Steigung ist anschaulich die Steigung der Tangente an die Funktion in der interessierenden Stelle:

$\includegraphics {chap9_1.eps}$

Die Steigung der Tangente an der Stelle $x_{0}$ bzw. in dem Punkt $(x_{0},f(x_{0}))$ schreiben wir als

$\begin{displaymath}f'(x_{0})=\frac{\Delta y}{\Delta x}\end{displaymath}$

und bezeichnen sie als Ableitung der Funktion f(x) an der Stelle $x_{0}$ . Diese Ableitung existiert keineswegs für jede Funktion in jedem Punkt. Betrachten wir die Betragsfunktion

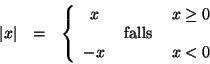
$\begin{displaymath} \begin{array}{ccc} \left\vert x\right\vert & = & \left\{ \be... ...athrm{falls}\: & \\ -x & & x<0 \end{array}\right. \end{array}\end{displaymath}$

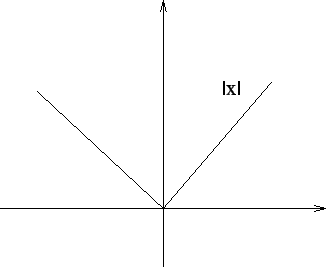
Deren Graph hat offensichtlich keine Tangente an der Stelle $x_{0}=0$ :

$\includegraphics {chap9_2.eps}$

Für die Ableitung der Funktion, d.h. der Funktion, die für alle $x$ die Ableitung an der jeweiligen Stelle $x$ angibt, läßt sich nur folgendes andgeben:

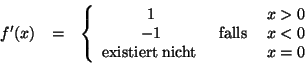
$\begin{displaymath} \begin{array}{ccc} f'(x) & = & \left\{ \begin{array}{ccc} 1 ... ...ert}\: \mathrm{nicht}\: & & x=0 \end{array}\right. \end{array}\end{displaymath}$

Für die Stelle $x=0$ läßt sich keine sinnvolle Tangente angeben. Die Ableitung einer Funktion definieren wir über einen Grenzwert. Anstatt direkt eine Tangentensteigung definieren zu wollen, geht man den indirekten Weg, indem man zuerst eine Sekantensteigung definiert, welche im Grenzwertübergang gerade die Tangentensteigung ergibt.

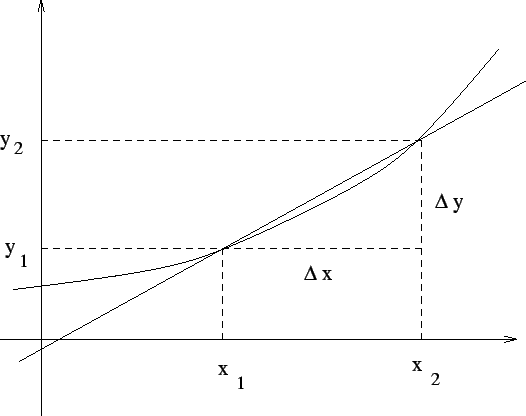
$\includegraphics {chap9_3.eps}$

Die Steigung einer Sekante durch $P(x_{1}\vert y_{1})$ ist definiert als

$\begin{displaymath}\frac{\Delta y}{\Delta x}=\frac{f(x_{2})-f(x_{1})}{x_{2}-x_{1}}\end{displaymath}$

Interessieren wir uns für die Tangentensteigung in $P(x_{1}\vert y_{1})$ , so machen wir den Grenzwertübergang

$\begin{displaymath}f'(x_{1}):=\lim _{x_{2}\to x_{1}}\frac{f(x_{2})-f(x_{1})}{x_{2}-x_{1}}\end{displaymath}$

Gleichbedeutend ist, daß wir eine Folge von Funktionswerten $\{x_{n}\}_{n}$ mit $\lim_{n\to\infty}x_n=x_0$ betrachten, so daß der Grenzwert

$\begin{displaymath}f'(x_{1}):=\lim _{n\to \infty }\frac{f(x_{n})-f(x_{1})}{x_{n}-x_{1}}\end{displaymath}$

die Ableitung ergibt. Existiert der Grenzwert dieser Folge für $n\to \infty$ , so gibt es die Steigung der Tangente, geschrieben als $f'$ . Hierbei muß man sich klarmachen, daß mit einer Folge, die gegen $x_{1}$ geht, eine beliebige mit dieser Eigenschaft gemeint ist, d.h. sie darf sich von rechts oder links nähern! Eine weitere äquivalente Schreibweise ist

$\begin{displaymath}f'(x_{1}):=\lim _{h\to 0}\frac{f(x_{1}+h)-f(x_{1})}{h}\end{displaymath}$

Falls der Grenzwert nicht existiert, so heißt $f$ nicht differenzierbar in $x_{1}.$

Bsp.:

$\begin{displaymath}f(x)=\vert x\vert\end{displaymath}$

mit $x_{0}=0$ und

$\begin{displaymath}x_{n}=(-1)^{n+1}\frac{1}{n}\end{displaymath}$

Für $n=2m,$ $m\in \mathbb {N}$ erfolgt Annäherung von links, denn $x_{2m}=-\frac{1}{2m}$ , es ist $\frac{f(-1/2m)-f(0)}{-1/2m-0}=-1$ .

Die Tangentensteigung ist also für alle $m$ genau $-1.$

Für $n=2m+1$ ergibt sich $x_{2m+1}=\frac{1}{2m+1}$ , also liegt Annäherung von rechts vor, mit dem Ergebnis: $\frac{f(1/(2m+1))-f(0)}{1/(2m+1)-0}=+1$

Also ist $\vert x\vert$ in $x_{1}=0$ nicht differenzierbar (es existiert keine Ableitung), da die rechts- und linksseitigen Grenzwerte verschieden sind. Ein weiteres

Bsp.:

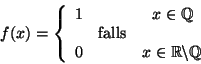
$\begin{displaymath}f(x)=\left\{ \begin{array}{ccc} 1 & & x\in \mathbb {Q}\\ & ... ...0 & & x\in \mathbb {R}\backslash \mathbb {Q}\end{array}\right. \end{displaymath}$

$f$ ist in keinem Punkt differenzierbar, da die Funktion nirgendwo stetig ist!

Äquivalente Schreibweisen für die Ableitung:

$\begin{displaymath}f'(x)=\frac{df}{dx}\quad \mathrm{falls}\: \mathrm{Funktion}\: \mathrm{von}\: \mathrm{x}\end{displaymath}$

$\begin{displaymath}\dot{f}(t)=\frac{df}{dt}\quad \mathrm{falls}\: \mathrm{Funktion}\: \mathrm{von}\: t\end{displaymath}$

oder z.B. für die Geschwindigkeit $\dot{x}=\frac{dx}{dt}$ . Dies zeigt die allgemeine Bedeutung der Ableitung auf, da die Ableitung die lokale Änderungsrate einer Funktion darstellt.