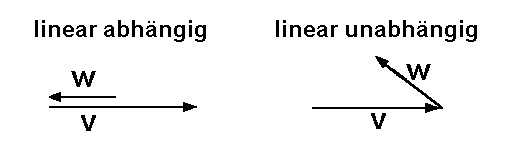
Lineare
Abhängigkeit von VektorenAndreas
Pester Fachhochschule Techikum
Kärnten, Villach
pester@cti.ac.at
Zusammenfassung: In
diesem Abschnitt wird die lineare Abhängigkeit von Vektoren definiert und an Beispielen erläutert
Stichworte: Definition | Beispiel für lineare Abhängigkeit | Beispiel für lineare Unabhängigkeit
Zwei Vektoren sind genau dann linear abhängig, wenn sie kollinear sind, oder anders gesagt: wenn zwei Vektoren parallel zueinander sind, dann sind sie linear abhängig, und wenn sie nicht parallel zu einander sind, dann sind sie linear unabhängig.
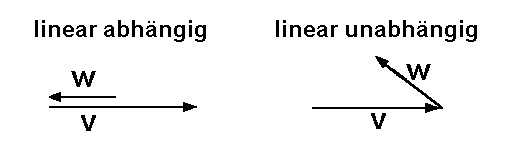
Bemerkungen
Es wird festgelegt: Der Nullvektor ist zu jedem Vektor parallel.
Zwei (oder mehrere) Vektoren sind genau dann kollinear, wenn sie (bei gleichem Anfangspunkt) auf einer Geraden liegen.
Vektoren nennt man komplanar, wenn sie in einer Ebene liegen.
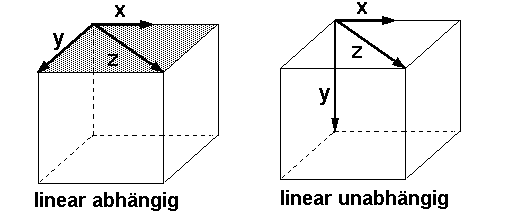
Drei Vektoren sind genau dann linear abhängig, wenn sie komplanar sind.
Bemerkungen
Es wird festgelegt: Der Nullvektor ist zu jeder Ebene parallel.
Zwei (oder mehrere) Vektoren sind genau dann komplanar, wenn sie bei gleichem Anfangspunkt in einer Ebene liegen.
Vier Vektoren im R3 (oder drei Vektoren im R2 ) sind immer linear abhängig.
Gegeben seien die zwei Vektoren v und w:
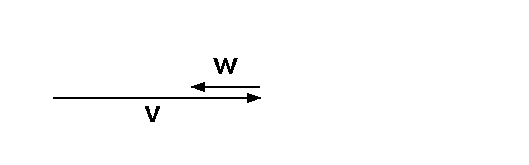
Wie man sieht, kann man mit ihnen außer der trivialen Nullsumme 0 = 0*v+0*w auch eine nichttriviale Nullsumme
0 = v + (-3)*w bilden:
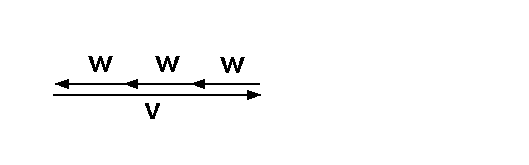
Somit sind die beiden Vektoren v und w linear abhängig.
Gegeben seien die zwei Vektoren v und w:
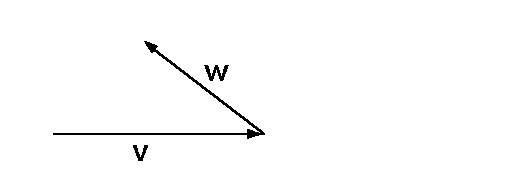
Wie man sieht kann man mit ihnen keine Nullsumme bilden, (außer der trivialen Nullsumme, die man ja immer bilden kann). Somit sind die beiden Vektoren v und w linear unabhängig.
Ist eine Menge {a, b, ...} linear abhängiger Vektorengegeben, so kann mindestens ein Vektor als Linearkombination der anderen Vektoren ausgedrückt werden.