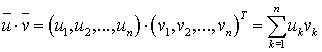
Vektoren im Rn
Andreas Pester Fachhochschule
Techikum Kärnten, Villach
pester@cti.ac.at
Zusammenfassung: In
diesem Abschnitt wird erläutert, wie man sinnvoll den Begriff eines Vektors auf
den Raum Rn erweitert
Stichworte: Übergang vom R3 zum Rn
Es gibt keine Notwendigkeit, Vektoren nur als Objekte im zwei- oder dreidimensionalen Raum zu betrachten. Dies ergab sich anfangs aus der vorrangigen Anwendung von Vektoren in der Geometrie und Physik.
Schon aus der Einführung der Matrizenrechnung und der Betrachtung von Vektoren als einspaltige oder einreihige Matrix ergab sich in natürlicherweise ein Übergang zur allgemeinen Dimension n. Viele aus der Vektorrechnung bekannte Operationen (bis auf das Kreuz- und Spatprodukt) ordnen sich nahtlos in die Matrizenrechnung ein.
Die Informatik und die digitale Signalverarbeitung schufen zusätzliche Anreize, die Vektorrechnung für den Rn zu entwickeln.
Vektoraddition und -subtraktion wurden unabhängig vom betrachteten Raum eingeführt, ebenso die Begriffe Betrag eines Vektors, Winkel, normierter Vektor, lineare Unabhängigkeit von Vektoren, Linearkombination von Vektoren sowie Multiplikation eines Vektors mit einer skalaren Grösse. Deshalb müssen sie nicht neu definiert werden.
Der Begriff des Skalarprodukts von zwei Vektoren u und v aus Rn kann koordinatenunabhängig ebenso definiert werden wie für 2- oder 3-dimensionale Räume, als u·v = |u|·|v|·cos(a).
Geht man zu einer Koordinatendarstellung von Vektoren über, so kann das Skalarprodukt zweier Vektoren so definiert werden: