hat
die Parameterdarstellung
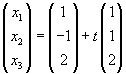
Ausgewählte Anwendungen der VektorrechnungAndreas
Pester Fachhochschule Techikum
Kärnten, Villach
pester@cti.ac.at
Zusammenfassung: In
diesem Abschnitt werden einige Anwendungen der Vektorrechnung aus Geometrie und Physik erklärt
, wenn
parallel zu
ist; d.h. wenn es
eine Zahl 
gibt mit
. Dies nennt man
die Punkt-Richtungs-Gleichung der Geraden. Wegen
lässt sich g in Bezug auf einen beliebigen Punkt P auch darstellen als
Beispiel:
| Die Gerade g durch A = (1,-1,2) in Richtung
hat
die Parameterdarstellung |
|
lautet für einen beliebigen Bezugspunkt P
ist genau dann parallel zu
, wenn
ist.
Angenommen, g ist die Wirklinie der Kraft
,
die bezüglich P das Moment 
besitzt.
Dann gilt nach der Formel
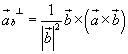
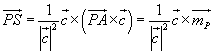
Das ist der Lotvektor von P auf g. Vergewissern Sie sich, dass
dies auch (bezüglich aller Vektorrichtungen) zutrifft. Dann ist die allgemeine
Momentengleichung einer Geraden g
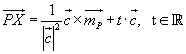
Beispiel:
Es sei durch folgenden Momentengleichung eine Gerade gbestimmt: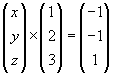
Die Richtung der Geraden ist
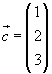Der Lotvektor aus dem Ursprung O auf g lautet
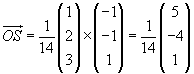S ist ein Geradenpunkt g mit S = (5/14, -4/14, 1/14)T. Die Parameterdarstellung
der Gerade g ist
Da der Lotvektor von P auf die Gerade g durch A in Richtung
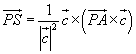lautet, beträgt der Abstand d
des Punktes P von g
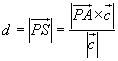(Überprüfen !)
Beispiel:
Man bestimme den Abstand den Punktes P = [1, 0, -1]T von der Geraden g = [2t, -t, 2t]T.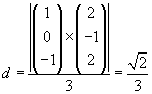
Man schaue sich folgende Demonstration an
Der Abstand von zwei Geraden
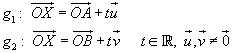ist durch folgende Formeln gegeben
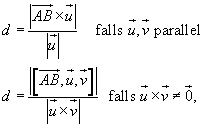Hier eine Online-Demonstration dieses Problems.
Aufgabe:
Man bestimme das Lot und den kürzesten Abstand folgender Geraden:
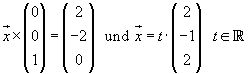(Lösung)
In der Physik sind die Anwendungen der Vektorrechnung sehr vielfältig, vor allem im Bereich der
Mechanik, Kinematik und Dynamik. Hier eine typische Aufgabe :
Ein Flugzeug fliegt mit konstanter Höhe und mit konstanter Geschwindigkeit von 680 km/h gegenüber Luft. Der Wind kommt aus westlicher Richtung (exakt!) und seine Geschwindigkeit ist 90 km/h. Der Winkel zwischen Flugzeugachse und Windrichtung (=pos. y-Richtung) beträgt 120°.